设函数(x)=sin(1-x)，则"(1)_________．

题目
设函数(x)=sin(1-x)，则"(1)_________．

相似考题

1.x→1时,sin(x)／(1－x^2)的极限是()。A.1B.0C./2D.1/2

2.设f(x)=sin2t+cost+arctant，则f1(t)=( )。

3.若∫f（x）dx＝F（x）＋C，则∫xf（1－x^2）dx＝（　　）。A． F（1－x^2）＋CB． －（1/2）F（1－x^2）＋CC． （1/2）F（1－x^2）＋CD． －（1/2）F（x）＋C

4.设f(x)=cos3x,则f'(x)=()。A、-sin3xB、-3sin3xC、sin3xD、3sin3x

参考答案和解析
答案：
解析：
【答案】0【考情点拨】本题考查了函数的高阶导数的知识点．
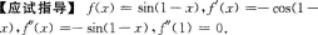
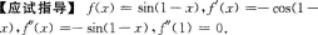
更多“设函数(x)=sin(1-x)，则"(1)_________．”相关问题

  • 第1题：

    设函数(x)=cos2x，则'(x)=()．

    A.2sin2x
    B.-2sin2x
    C.sin2x
    D.-sin2x

    答案：B
    解析：
    '(x)=(cos2x)'=-sin2x·(2x)'=-2sin2x．

  • 第2题：

    设函数y=sin2x，则y"=_____．


    答案：
    解析：
    填-4sin2x．y'=2cos2x．y＂=-4sin2x．

  • 第3题：

    设函数(x)=1+sin2x，求'(0)．


    答案：
    解析：
    '(x)=2cos2x，所以'(0)=2．

  • 第4题：

    若函数y=(x)在[-1，1]上是单调函数，则使得y=(sinx)必为单调函数的区间是（ ）

    A.R
    B.[-1，1]
    C.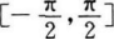
    D.[-sin1，sin1]


    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为函数的单调区间． 1应试指导】y=(x)在[-1，1]上是单调函数，∴y=(x)的单调区间为[-1，1]，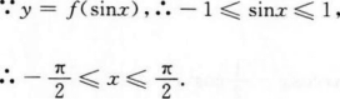

  • 第5题：

    已知函数?(x)=(sin x-cos x)sin x，x∈R，则?(x)的最小正周期是__________．


    答案：
    解析：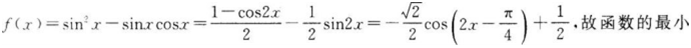

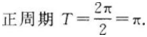
  • 第6题：

    设4／（1-x2）·f（x）=d／dx［f（x）］2，且f（0）=0，则f（x）等于：（）

    • A、（1+x）／（1-x）+c
    • B、（1-x）／（1+x）+c
    • C、1n｜（1+x）／（1-x）｜+c
    • D、1n｜（1-x）／（1+x）｜+c

    正确答案:C

  • 第7题：

    设函数y＝e2xcos3x，则dy＝（）。

    • A、e2x（2cos3x-3sin3x）
    • B、e2x（2cos3x-3sin3x）dx
    • C、-6e2xsin3xdx
    • D、e2x（2cos3x+3sin3x）dx

    正确答案:B

  • 第8题：

    若f′（cos2x）=sinx，则f（x）等于：（）

    • A、（1／3）（1-x）3+c
    • B、（2／3）（1-x）3+c
    • C、-（1／3）（1-x）3+c
    • D、（1-x）3+c

    正确答案:C

  • 第9题：

    单选题
    设f（x）的一个原函数为cosx，g（x）的一个原函数为x2，则f［g（x）］等于：（）
    A

    cosx2

    B

    -sinx2

    C

    cos2x

    D

    -sin2x


    正确答案： A
    解析： 利用原函数定义，求出f（x）、g（x）；利用复合函数关系求出f[g（x）]。

  • 第10题：

    填空题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

    正确答案： 1/sin2(sin1)
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第11题：

    单选题
    若f′（cos2x）=sinx，则f（x）等于：（）
    A

    （1／3）（1-x）3+c

    B

    （2／3）（1-x）3+c

    C

    -（1／3）（1-x）3+c

    D

    （1-x）3+c


    正确答案： D
    解析： 把式子右边变形或用变量替换方法，得f′（x）=（1-x）2，再积分。

  • 第12题：

    单选题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。
    A

    1/sin2（sin1）

    B

    sin2（sin1）

    C

    －sin2（sin1）

    D

    －1/sin2（sin1）


    正确答案： B
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第13题：

    设函数y=sin(x2-1)，则dy等于()．

    A.cos(x2-1)dx
    B.-cos(x2-1)dx
    C.2xcos(x2-1)dx
    D.-2xcos(x2-1)dx

    答案：C
    解析：
    dy=y'dx=cos(x2-1)(x2-1)'dx=2xcos(x2-1)dx

  • 第14题：

    设函数y=sin(2x+1)，则y"=_____．


    答案：
    解析：
    填-4sin(2x+1)．

  • 第15题：

    设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.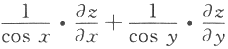


    答案：
    解析：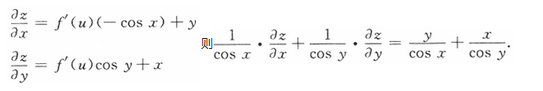

  • 第16题：

    设函数f(x)=COS2x，则f′(x)=()．

    A.2sin2x
    B.-2sin2x
    C.sin2x
    D.-sin2x

    答案：B
    解析：
    由复合函数求导法则，可得故选B．

  • 第17题：

    设函数y=f(x)为最小正周期为π的奇函数，则f(x)可能是( )。

    A.f(x)=sinx
    B.f(x)=tan2x
    C.f(x)=sin(2x+π/2)
    D.f(x)=sinxcosx

    答案：D
    解析：

  • 第18题：

    设x=1，以下函数返回值最大的是（）。

    • A、Sin（x）
    • B、Exp（x）
    • C、Sqr（x）
    • D、Log（x）

    正确答案:B

  • 第19题：

    设f′（cosx）=sinx，则f（cosx）等于（）

    • A、-cosx+c
    • B、cosx+c
    • C、1／2（sin2x／2-x）+c
    • D、1／2（2sin2x-x）+c

    正确答案:C

  • 第20题：

    单选题
    设f′（cosx）=sinx，则f（cosx）等于（）
    A

    -cosx+c

    B

    cosx+c

    C

    1／2（sin2x／2-x）+c

    D

    1／2（2sin2x-x）+c


    正确答案： C
    解析： 暂无解析

  • 第21题：

    单选题
    设f（x）＝sinx，f[φ（x）]＝1－x2，则φ（x）＝（　　）。
    A

    arcsin（1－x）

    B

    arcsin（1＋x）

    C

    arcsin（1－x2）

    D

    arcsin（1＋x2）


    正确答案： C
    解析：
    因sin（arcsinx）＝x，又知f（x）＝sinx，f[φ（x）]＝1－x2，故φ（x）＝arcsin（1－x2）。

  • 第22题：

    单选题
    设4／（1-x2）·f（x）=d／dx［f（x）］2，且f（0）=0，则f（x）等于：（）
    A

    （1+x）／（1-x）+c

    B

    （1-x）／（1+x）+c

    C

    1n｜（1+x）／（1-x）｜+c

    D

    1n｜（1-x）／（1+x）｜+c


    正确答案： A
    解析： 计算等号右边式子，得到f′（x）表达式。计算不定积分。

  • 第23题：

    单选题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。
    A

    sin2（sin1）

    B

    1/sin2（sin1）

    C

    sin（sin1）

    D

    1/sin（sin1）


    正确答案： D
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

相关内容