盒子中有5个产品，其中恰有3个合格品．从盒子中任取2个，记X为取出的合格品个数．求 (1)X的概率分布； (2)EX．

题目
盒子中有5个产品，其中恰有3个合格品．从盒子中任取2个，记X为取出的合格品个数．求
(1)X的概率分布；
(2)EX．

相似考题

1.一个盒子中有4个球,球上分别标有号码0,1,1,2,从盒子中有放回的任意取出2个球,设X为取出的球上的号码的乘积,(1)求X的分布列;(2)P(X

2.在一个制造过程中,不合格率为0.05,如今从成品中随机取出10个,记x为10个成品中的不合格品数,恰有一个不合格品的概率P(x=1)为________。A．0.125B．0.315C．-0.05D．1.05

3.设有100个圆柱形零件，其中95个长度合格，92个直径合格，87个长度直径都合格，现从中任取一件该产品，求:(1)该产品是合格品的概率;(2)若已知该产品直径合格，求该产品是合格品的概率;(3)若已知该产品长度合格，求该产品是合格品的概率。

4.一批产品共有10件,其中有两件是不合格品,随机抽取3件,求(1)其中至少有1件不合格品的概率;(2)三件都是合格品的概率。

更多“盒子中有5个产品，其中恰有3个合格品．从盒子中任取2个，记X为取出的合格品个数．求 ”相关问题

  • 第1题：

    一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少?


    参考答案：

  • 第2题：

    在一个制造过程中，其产品的不合格品率为0.03，随机抽取9件产品，其中恰有1件不合格品的概率为（ ）。

    A.0.2116

    B.0.4796

    C.0.5204

    D.0.8489


    正确答案：A
    A。

  • 第3题：

    设一批产品的不合格品率为0.1，从中任取3件，记x为其中的不合格品数，下列概率计算正确的有（ ）。

    A.P(X=2)=0.027

    B.P(X=O)=0

    C.P(X≤1)=0.972

    D.P(X<3)=1

    E.P(0≤X≤3)=1


    正确答案：ACE
    ACE。

  • 第4题：

    盒子中装有10个晶体管，其中7个是一级品.从盒子中任意取2次，每次1个.在下列两种情形下，分别求取出的晶体管中恰有1个是一级品的概率.(1)先取出的晶体管不放回盒子；第二次取到一级品的概率等于( ).

    A.6/9
    B.7/9
    C.7/10
    D.6/10

    答案：C
    解析：
    这是一个典型的“抽签”(俗称抓阄)模型，这类问题必定满足“抽到的概率与次序 无关”，由于第一次取到一级品的概率为0.7，因此第二次取到一级品的概率也是0.7.故选C.

  • 第5题：

    10个相同的盒子中分别装有1—10个球，任意两个盒子中的球数都不相同，小李分三次，每次取出若干个盒子，每次取出的盒子中的球数之和都是上一次的3倍，且最后剩下一个盒子。剩下的盒子中有多少个球？

    A.9
    B.6
    C.5
    D.3

    答案：D
    解析：
    第一步，本题考查其他杂题。
    第二步，设第一次取出的球数之和为x，则第二次为3x，第三次为9x。最后剩下的盒子球数为y。
    第三步，所有球的数字之和为1+2+3+4+5+6+7+8+9+10=55。则有x+3x+9x+y=55，化简为13x+y=55。
    第四步，使用代入排除法，只有D项y=3代入，解得x=4，满足题意。

  • 第6题：

    从一批产品中任意抽取10件，检验其中不合格品的数目，事件A= “不合格品恰为3件”与事件B= “不合格品少于5件”的关系为（ ）。


    答案：A
    解析：
    。不合格品为3件，一定少于5件。

  • 第7题：

    已知甲、乙两箱中装有同种产品，其中甲箱中装有3件合格品和3件次品，乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后，求：
    　　(1)乙箱中次品件数X的数学期望；
    　　(2)从乙箱中任取一件产品是次品的概率.


    答案：
    解析：

  • 第8题：

    10件产品中有4件不合格，从中任取两件，已知取出的两件中有一件不合格，则另一件也是不合格品的概率是（ ）。


    答案：D
    解析：

  • 第9题：

    在一个制造过程中，不合格率为0. 05，如今从成品中随机取出10个，记X为10个成品中的不合格品数，恰有一个不合格品的概率P（X = 1）=（）。
    A. -0.05 B. 0. 125 C. 0.315 D. 1.05


    答案：C
    解析：

  • 第10题：

    一批产品的不合格品率为0.07，现从中随机抽取7个，其中恰有一个不合格品的 概率为（ ）。


    答案：C
    解析：

  • 第11题：

    问答题
    3.设在15个同类型的零件中有2个是次品，从中任取3次，每次取1个，取后不放回．以X表示取出的次品的个数，求X的分布律．

    正确答案：
    解析：

  • 第12题：

    单选题
    有一批混凝土预制构件，已知每8件中有3件不合格品，若从该批产品中任取5件，问恰好有2件不合格品概率为（）。
    A

    0.26

    B

    0.34

    C

    0.16

    D

    0.69


    正确答案： D
    解析： 暂无解析

  • 第13题：

    一批产品的不合格品率为0.2,现从这批产品中随机抽取5个,记X为这5个产品中的不合格品数,则这5个产品中没有合格品的概率为________。

    A．

    B．

    C．

    D．


    正确答案：A

  • 第14题：

    一批产品的不合格品率为0.07，现从中随机抽取7个，其中恰有一个不合格品的概率为（ ）。

    A.

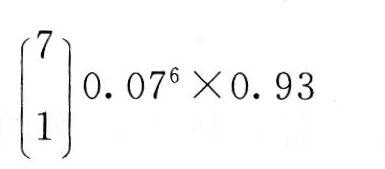
    B.

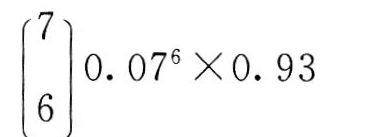
    C.

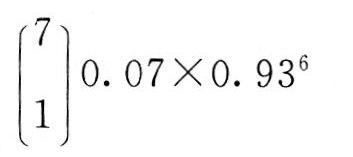
    D.


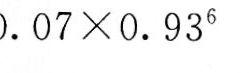    正确答案：C
    C。

  • 第15题：

    一批产品的不合格品率为0.2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为( )。


    正确答案：B
    解析：

  • 第16题：

    一批零件中有10个合格品，3个次品，安装机器时，从这批零件中任取一个，取到合格品才能安装．若取出的是次品，则不再放回，求在取得合格品前已取出的次品数X的概率分布．


    答案：
    解析：
    由题意，X的可能取值为0，1，2，3．X=0，即第一次就取到合格品，没有取到次品，P{X=0}=；X=1，即第一次取到次品，第二次取到合格品，P{X=1}=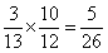；同理，P{X=2)=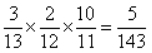；P{X=3}=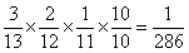

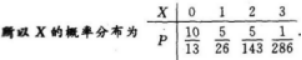
  • 第17题：

    设5个产品中有3个合格品、2个不合格品，从中不放回地任取2个，则取出的2 个产品中恰有1个合格品的概率为（ ）。
    A. 0. 1 B. 0. 3

    C. 0. 5 D. 0. 6


    答案：D
    解析：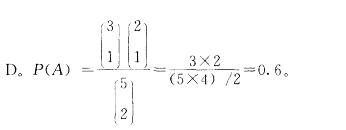

  • 第18题：

    某车间的一条生产线，正常运转的概率为90%，不正常运转的概率为10%。正常运转时，生产95%的合格品和5%的不合格品；不正常运转时，生产10%的合格品和90%的不合格品。从产品中任取一件检查，则：
    此产品是合格品的概率为（ ）。
    A. 0. 3333 B. 0.8550 C. 0.8650 D. 0.9884


    答案：C
    解析：
    设事件A ={生产线正常运转}，则P(A) =90%，P(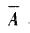) = 10% ；设事件B ={产品是合格品}，则P(B) =P(AB +B) =P(AB) + P(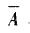B) =P(A)P(B A) + P () P （B 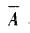) =0.90 x0.95 +0. 10 x0. 10 = 0. 8550 + 0. 010 = 0. 8650。

  • 第19题：

    有三个盒子,第一个盒子有4个红球1个黑球,第二个盒子有3个红球2个黑球,第三个盒子有2个红球3个黑球,如果任取一个盒子,从中任取3个球,以X表示红球个数.
    　　(1)写出X的分布律；(2)求所取到的红球数不少于2个的概率.


    答案：
    解析：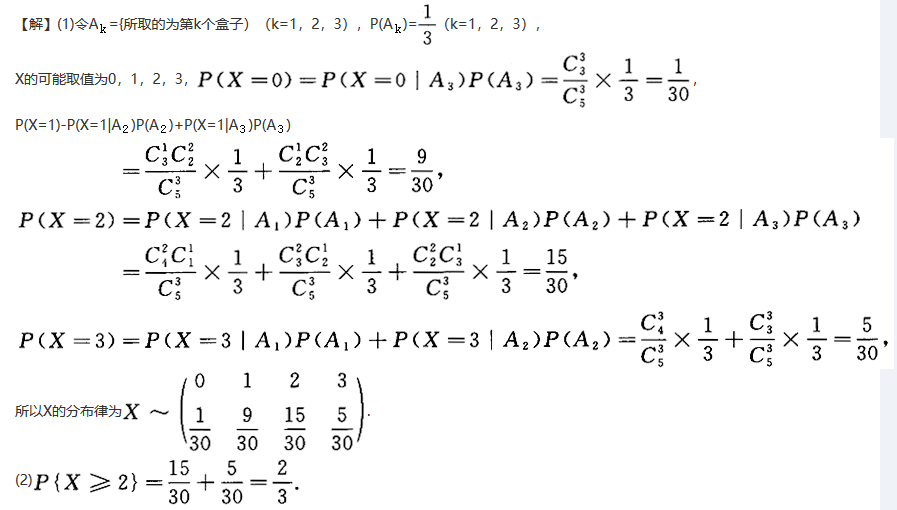

  • 第20题：

    一批产品的不合格品率为0. 2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为（ ）。



    答案：B
    解析：

  • 第21题：

    设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（ ）。[2008年真题]
    A. P(X=2) =0.027 B. P(X=0) =0
    C. P(X ≤l) =0.972 D. P(XE. P(0 ≤X ≤3) =1


    答案：A,C,E
    解析：
    不合格品数X有四种可能，则其概率分别为：P(X=0) =0.9×0.9×0.9 =0.729; P(X = l) = 3×0. 1×0. 9×0. 9 = 0. 243 ； P(X = 2) =3×0. 1×0. 1×0.9 =0.027； P(X =3) =0. 1×0. 1×0. 1 =0.001。所以，P(X≤l) =P(X=0) +P(X=1) =0. 972, P(0≤X≤ 3) = P(X = 0) +P(X = 1) +P(X = 2) +P(X=3) =1。

  • 第22题：

    设10件产品有4件不合格品，从中任取两件，已知所取两件产品中有一件是不合格品，则另一件也是不合格品的概率是（）.


    正确答案:1/5

  • 第23题：

    多选题
    设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（　　）。[2008年真题]
    A

    P（X=2）=0.027

    B

    P（X=0）=0

    C

    P（X≤1）=0.972

    D

    P（X＜3）＝1

    E

    P（0≤X≤3）=1


    正确答案： B,E
    解析： 不合格品数X有四种可能，则其概率分别为:P（X=0）=0.9×0.9×0.9=0.729；P（X=1）=3×0.1×0.9×0.9=0.243；P（X=2）=3×0.1×0.1×0.9=0.027；P（X=3）=0.1×0.1×0.1=0.001。所以，P（X≤1）=P（X=0）+P（X=1）=0.972，P（0≤X≤3）= P（X=0）+P（X=1）+P（X=2）+P（X=3）=1。

相关内容