一次性收付款项的折现率计算公式为( )。A．(P/F)1/n＋1B．(P/F)n-1C．(F/P)1/n-1D．(F/P)n-l

题目

一次性收付款项的折现率计算公式为( )。

A．(P/F)1/n＋1

B．(P/F)n-1

C．(F/P)1/n-1

D．(F/P)n-l

相似考题

1.单利本利和计算公式为( )。A．F＝P(1+i)nB．F=P(1+i·n)C．F=P·inD．F=P·i·n

2.复利终值的计算公式是()。A. F=P?(1+i)B. F=P?(FVIF,k,n)C. F=P?(PVIFA,k,n)D. F=P?(FVIF,k,,n+1)

3.资金成本用相对数表示称之为资金成本率，计算公式为()A、K=D/(P+F)B、K=D/P(1-f)C、K=D/2(P-F)D、K=D/P(1+f)

4.对前m期没有收付款项，后"期每期未有相等金额的系列收付款项的递延年金而言，其现值计算公式有( )。A．P＝A×(P/A，i，n)×(P/F，i，m)B．P＝A×(F/A，i，n)×(P/F，i，m+n)C．P＝A×(P/A，i，n)×(P/A，i，m)D．P＝A×[(P/A，i，m+n)-(P/F，i，m)]

更多“一次性收付款项的折现率计算公式为( )。A.(P／F)1／n＋1B.(P／F)n－1C.(F／P)1／n－1D.(F／P)n－l ”相关问题

  • 第1题：

    单利本利和计算公式为( )。

    A．F=P(1+i)n

    B．F=P(1+in)

    C．F=Pin

    D．F=Pin


    正确答案：A

  • 第2题：

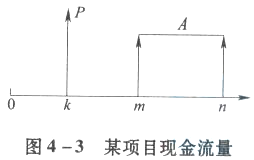
    某建设项目现金流量图见图4-3，基准折现率为i，则该项目在k时点的现值P的表达式正确的有（ ）。


    A：P=A(P/A,i,n-m+1)(P/F,i,m-k-1)
    B：P=A(P/A,i,n-m+1)(P/F,i,n-k)
    C：P=A(F/A,i,n-m+1)(P/F,i,m-k-1)
    D：P=A(F/A,i,n-m+1)(P/F,i,n-k)
    E：P=A(P/A,i,n-k)-A(P/A,i,m-k-1)

    答案：A,D,E
    解析：
    2019版教材P163
    本题中，将已知的年金折算为一点有三种方法：一种是将年金往前折算，折算到m-1年末，然后再一起往k点折算；此时共有n-（m-1）个年金，从m-1到k共计息（m-1-k）次，因此P=A(P/A，i，n-m+1)（P/F，i，m-k-1）。第二种方法是将年金往后折算，折算到第n年末。然后再一起往k点折算；从n到k共计息（n-k）次。因此P=A（F/A，i，n-m+1）（P/F，i，n-k)。第三种方法如图4-4所示，在k+1与m-1增加一个等额年金A，再减去等额年金A。则k+1到n年有等额现金流入，k+1到m-1年有等额现金流出，因此P为两个年金现值的差。

  • 第3题：

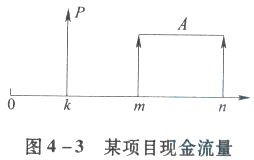
    某建设项目现金流量图见图4-3，基准折现率为i，则该项目在k时点的现值P的表达式正确的有（ ）。


    A.P=A(P/A,i,n-m+1)(P/F,i,m-k-1)
    B.P=A(P/A,i,n-m+1)(P/F,i,n-k)
    C.P=A(F/A,i,n-m+1)(P/F,i,m-k-1)
    D.P=A(F/A,i,n-m+1)(P/F,i,n-k)
    E.P=A(P/A,i,n-k)-A(P/A,i,m-k-1)

    答案：A,D,E
    解析：
    2020版教材P163
    本题中，将已知的年金折算为一点有三种方法：一种是将年金往前折算，折算到m-1年末，然后再一起往k点折算；此时共有n-（m-1）个年金，从m-1到k共计息（m-1-k）次，因此P=A(P/A，i，n-m+1)（P/F，i，m-k-1）。第二种方法是将年金往后折算，折算到第n年末。然后再一起往k点折算；从n到k共计息（n-k）次。因此P=A（F/A，i，n-m+1）（P/F，i，n-k)。第三种方法如图4-4所示，在k+1与m-1增加一个等额年金A，再减去等额年金A。则k+1到n年有等额现金流入，k+1到m-1年有等额现金流出，因此P为两个年金现值的差。

  • 第4题：

    设P为债券价格，F为面值，r为到期收益率，n是债券期限。如果按年复利计算，零息债券到期收益率的计算公式为()。

    A:r=(P／F)1/n一1
    B:r=(F／P)1/n一1
    C:r=(P／F一1)1/n
    D:r=(F／P一1)1/n

    答案：B
    解析：
    本题考查零息债券到期收益率的计算公式。

  • 第5题：

    一次性收付款项的复利终值的计算公式为（　　）。

    A.F=[A?(1+i)n-1]／i
    B.F=P(1+i)n
    C.F=A?(F／A，I，n)
    D.F=[(1+i)n-1]／i

    答案：B
    解析：
    一次性收付款项的复利终值。在某一特定时点上一次性支付(或收取)，经过一段时间后再相应地一次性收取(或支付)的款项，即为一次性收付款项。终值又称将来值，是现在一定量现金在未来某一时点上的价值，俗称本利和。假设：i为即期利率；n为计息周期数：P为现值：F为终值，则复利终值的计算公式为：F=P(1+i)n=P(F／P，i，n)式中：(1+i)n称为复利终值系数，记为(F／P，i，n)。终值系数可通过查复利终值系数表获得。

相关内容