若采用折中原则计算(最大值系数α＝0．7)，生产C型汽车能使公司获得的经济效益为（ ）万元。 A．450 B．490 C．500 D．550

题目

若采用折中原则计算(最大值系数α＝0．7)，生产C型汽车能使公司获得的经济效益为（ ）万元。 A．450 B．490 C．500 D．550

相似考题

1.若采用折衷原则计算（最大值系数a=0.7），生产C型汽车能使公司获得的经济效益为（ ）万元。A. 450 B. 490C. 500 D. 550

2.若根据折中原则进行决策(最大值系数α=0．85)，生产B果汁能使该农场获得的经济效益为（ ）万元。A．25.50 B．59.50 C．61.75 D．72.25

3.若采用后悔值原则计算，使公司获得最大经济效益的车型为（ ）A．A型汽车B．B型汽车C．C型汽车D．B型汽车和C型汽车

4.若采用后悔值原则计算，使公司获得最大经济效益的车型为（ ）A. A型汽车 B. B型汽车C. C型汽车 D. B型汽车和C型汽车

参考答案和解析
正确答案：C
本题考查不确定型决策方法。采取折中原则C型汽车可以获得的经济效益为800×0．7＋(－200)×(1－0．7)＝500(万元)。
更多“若采用折中原则计算(最大值系数α=0.7),生产C型汽车能使公司获得的经济效益为( )万元。 A.450 B.4 ”相关问题

  • 第1题：

    若采用折衷原则进行计算(最大值系数α＝0．85)，若采用中批量Ⅱ生产，该厂获得的经济效益为（ ）。

    A．310

    B．327．5

    C．350

    D．375．5


    正确答案：B
    采用折衷原则计算，中批量Ⅱ生产方案可以获得的经济效益为350×0．85＋200×0．15＝327．5。故选B。

  • 第2题：

    若采用折中原则计算(最大值系数a=0．7)，若采用大批量生产，使公司获得的经济效益为（　　）万元。

    A.30
    B.35．5
    C.30．5
    D.25．5

    答案：C
    解析：
    采取折中原则大批量生产可以获得的经济效益为35×0．7+20×(1—0．7)=30．5(万元)。

  • 第3题：

    某公司ABC三型汽车经营损益表（单位：万元）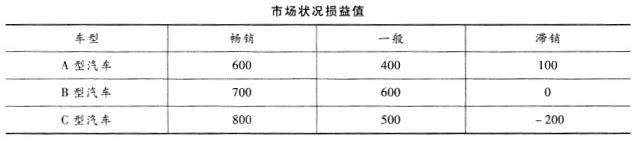

    若采用后悔值原则计算，使公司获得最大经济效益的车型为()。

    A:A型汽车
    B:B型汽车
    C:C型汽车
    D:B型汽车和C型汽车

    答案：B
    解析：
    采取后悔值原则计算如下：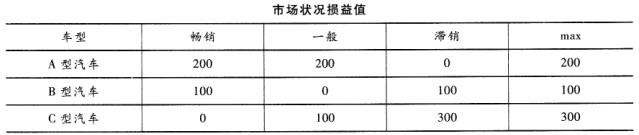

    各方案的最大后悔值为{200，100，300}，取其中最小值min{200，100，300}=100，对应的B型汽车为选取方案，因此本题选B。第一步，计算损益值的后悔值矩阵，方法是用各自然状态下的最大损益值分别减去该状态下所有方案的损益值，从而得到对应的后悔值。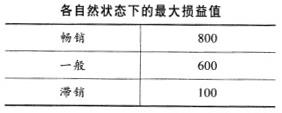

    然后算后悔值：

    第二步，选择最大后悔值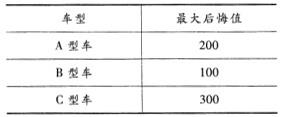

    第三步，最大后悔值中选择最小值，所以选B车型，最大后悔值为100。

  • 第4题：

    若采用折中原则计算(最大系数仅=0．7)，生产c型汽车能使公司效益为（ ）万元。A．450 B．490C．500 D．550


    正确答案：C
    最大系数为0.7，则最小系数为0.3，效益为800×0.7—200×0.3：500万元。

  • 第5题：

    若采用折中原则计算(最大值乐观系数a=0．7)，生产C型汽车能使公司获得的经济效益为（　　）万元。

    A.450
    B.490
    C.500
    D.550

    答案：C
    解析：
    采取折中原则，生产C型汽车可以获得的经济效益为800×0．7+(-200)×(1-0．7)=500(万元)。

相关内容