为分析某市城镇居民1995年～2003年人均可支配收入和人均消费性支出之间的关系，取得如下统计资料：请根据以上资料进行计算和分析判断，从备选答案中选出正确答案。A．B．C．当人均可支配收入增加1元时，人均消费性支出将平均增长0.7209元D．当人均可支配收人增加1元时，人均消费性支出将增长0.7209元

题目

为分析某市城镇居民1995年～2003年人均可支配收入和人均消费性支出之间的关系，取得如下统计资料：

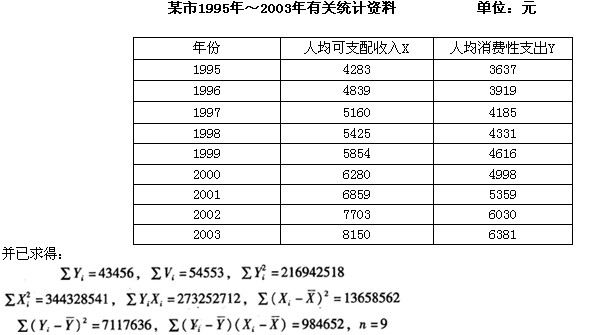
请根据以上资料进行计算和分析判断，从备选答案中选出正确答案。

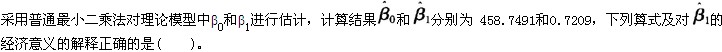
A．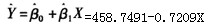

B．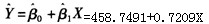

C．当人均可支配收入增加1元时，人均消费性支出将平均增长0.7209元

D．当人均可支配收人增加1元时，人均消费性支出将增长0.7209元

相似考题

1.对2009年我国13个省市自治区城镇居民人均消费支出与人均可支配收入的相关系数进行显著性检验时，t的检验值为28.51，tα/2=2.201，则下列说法正确的有( )。(α=0.05)A．拒绝H0B．接受H0C．人均消费性支出与人均可支配收入之间存在显著的线性相关关系D．人均消费性支出与人均可支配收入之间不存在显著的线性相关关系E．无法判断人均消费性支出与人均可支配收入之间是否存在显著的线性相关关系

2.（三）为分析某市城镇居民1995年——2003年人均可支配收入和人均消费性支出之间的关系，取得如下统计资料：

3.估计的城镇居民家庭人均可支配收入和人均消费的一元线性直线回归方程式：人均消费Y=1300+0.79X，则当城镇居民家庭人均可支配收入是15000元，人均消费支出是（ ）元。A.13000 B.13150 C.12560 D.15000

4.下列变量中，哪些是相对应的解释变量和被解释变量?( )A．居民人均可支配收入和人均消费性支出B．消费品价格水平和人均消费性支出C．银行存款利率和人均消费性支出D．消费者偏好和人均消费性支出E．消费者身高和人均消费性支出

更多“ 为分析某市城镇居民1995年～2003年人均可支配收入和人均消费性支出之间的关系，取得如下统计资料：请根据以上资料进行计算和分析判断，从备选答案中选出正确答案。A．B．C．当人均可支配收入增加1元时，人均消费性支”相关问题

  • 第1题：

    根据抽样调查数据对人均消费和人均可支配收入进行回归分析，得到估计的一元线性回归模型Y=1000+0．7X(X：人均可支配收入，Y：人均消费；单位均为元)。关于该回归模型的说法，正确的有()。

    A.人均可支配收入每增加1元，人均消费将平均增长0．7元
    B.人均可支配收入每减少1元，人均消费将平均增长0．7元
    C.人均可支配收入每增加1％，人均消费将平均增长0．7％
    D.人均可支配收入每减少1％，人均消费将平均增长0．7％
    E.当人均可支配收入为20000元时，人均消费将为15000元

    答案：A,E
    解析：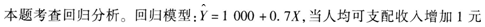

    时，人均消费增加=1000+0．7×(X+1)-(1000+0．7X)=0．7(元)。选项A正确，选项B错误。当人均可支配收入增加1％，人均消费增长=[1000+0．7×(1+1％)-(1000+0．7X)]÷(1000+0．7X)=0．7％X÷(1000+0．7)。选项C、D错误。当X=2000时，代入回归模型中，得到Y=1500，选项E正确。

  • 第2题：

    利用样本数据拟合城镇居民人均可支配收入X(单位：元)和人均消费Y(单位：元)的回归方程，估计方程Y=1293+0.6X，R2为0.99，说法正确的有（ ）。

    A.城镇居民家庭人均可支配收入每增加1元，城镇居民人均消费增加0.6元
    B.城镇居民家庭人均可支配收入每增加1元，城镇居民人均消费增加1293元
    C.城镇居民可支配收入对人均消费支出的变化的解释能力较差
    D.城镇人均可支配收入可以很好地解释人均消费支岀的变化
    E.城镇居民家庭人均可支配收入X=20000元时，人均消费支出Y预估为13293元

    答案：A,D,E
    解析：
    回归分析中，被预测或被解释的变量称为因变量， 一般用Y 表示;用来预测或解释因变量的变量称为自变量， 一般用X 表示。方程Y=1293+0.6X，可得出家庭人均可支配收入每增加1元，城镇居民人均消费增加0.6元。（选项A正确）决定系数，也称为R2 ，可以测度回归直线对样本数据的拟合程度，决定系数的取俏在0 - 1 之间，大体上说明了回归模型所能解释的因变量变化占因变量总变化的比例。决定系数越高模型的拟合效果就越好，即模型解释因变量的能力越强。（选项C错误）
    R2 为0.99，说明回归模型的拟合效果很好，即城镇人均可支配收入可以很好地解释人均消费支出的变化。（选项D正确）
    将X=15000.0元代入回归方程，得：Y=1293+0.6X=1293+12000=13293元。（选项E正确）

  • 第3题：

    利用样本数据拟合城镇居民人均可支配收入X（单位：元）和人均消费Y（单位：元）的回归方程，估计方程Y=1293+0.6X，R2为0.99，说法正确的有（ ）。

    A.城镇居民家庭人均可支配收入每增加1元，城镇居民人均消费增加0.6元
    B.城镇居民家庭人均可支配收入每增加1元，城镇居民人均消费增加1293元
    C.城镇居民可支配收入对人均消费支出的变化的解释能力较差
    D.城镇人均可支配收入可以很好地解释人均消费支岀的变化
    E.城镇居民家庭人均可支配收入X=20000元时，人均消费支出Y预估为13293元

    答案：A,D,E
    解析：
    回归分析中，被预测或被解释的变量称为因变量， 一般用Y 表示;用来预测或解释因变量的变量称为自变量， 一般用X 表示。方程Y=1293+0.6X，可得出家庭人均可支配收入每增加1元，城镇居民人均消费增加0.6元。（选项A正确） 决定系数，也称为R2 ，可以测度回归直线对样本数据的拟合程度，决定系数的取俏在0 - 1 之间，大体上说明了回归模型所能解释的因变量变化占因变量总变化的比例。决定系数越高模型的拟合效果就越好，即模型解释因变量的能力越强。（选项C错误）
    R2 为0.99，说明回归模型的拟合效果很好，即城镇人均可支配收入可以很好地解释人均消费支出的变化。（选项D正确）
    将X=15000.0元代入回归方程，得：Y=1293+0.6X=1293+12000=13293元。（选项E正确）

  • 第4题：

    根据抽样调查数据对人均消费和人均可支配收入进行回归分析,得到估计量的一元回归线模型Y=1000+0.7X(X为人均可支配收入,Y为人均消费额),关于该回归模型的说法，说法正确的是()。

    A.人均可支配收入每减少1元,人均消费平均增长0.7元
    B.人均可支配收入每增加1元,人均消费平均增长0.7元
    C.人均可支配收入每增加1%,人均消费平均增长0.7%
    D.当人均可支配收入为20000元时,人均消费将为15000元
    E.人均可支配收入每减少1%,人均消费将平均增长0.7

    答案：B,D
    解析：
    此题考查一元线性回归模型。当人均可支配收入增加1元,Y增加额=(1000+0.7×2)-(1000+0.7×1)=0.7元,选项B正确。当人均可支配收入为20000元时,Y=1000+0.7×20000=15000元,选项D正确。

  • 第5题：

    根据抽样调查数据中人均收入和人均可支配消费进行回归分析，得到估计的一元线性回归模型Y=1000+0.7X，（X，人均可支配收入；Y，人均消费，单位为元），关于该回归模型的说法，正确的是（）。

    A. 人均可支配收入每增加1元，人均消费将平均增长0.7元
    B. 人均可支配收入每减少1元，人均消费将平均增长0.7元
    C. 人均可支配收入每增加1元，人均消费将平均增长0.7%
    D. 当人均可支配收入为20000元时，，人均消费将为15000
    E. 人均可支配收入每减少1%，人均消费将平均增长7%

    答案：A,D
    解析：
    考核第25章回归方程。
    Y=1000+0.7X，X为人均收入、Y为人均消费。
    当人均可支配收入增加1元时，Y增加额=（1000+0.7×1）-（1000+0.7×2）=0.7*增加的X=0.7×1=0.7，即当人均可支配收入每增加1元，人均消费将平均增长0.7元。A选项正确。
    当人均可支配收入为20000元时，人均消费=1000+0.7×20000=15000元。D选项正确。

相关内容