正态概率纸的作用有( )。A.判断一个样本是否来自正态总体B.若确定是正态分布，可估计正态均值与正态标准差C.可用来检验一个样本是否来自对数正态总体D.用来检验一个样本是否来自二项分布

题目

正态概率纸的作用有( )。

A.判断一个样本是否来自正态总体

B.若确定是正态分布，可估计正态均值与正态标准差

C.可用来检验一个样本是否来自对数正态总体

D.用来检验一个样本是否来自二项分布

相似考题

1.正态概率纸的用途是（ ）。A．检验一个样本是否来自正态总体B．若确定是正态分布，可估计正态均值与正态标准差C．可用来检验一个样本是否来自对数正态分布D．用来检验一个样本是否来自二项分布

2.正态概率纸的用途有( )。A．检验一个样本是否来自正态分布B．检验一个样本是否来自对数正态分布C．检验一个样本是否来自二项分布D．检验一个样本是否来自任一个分布E．在确认样本来自正态分布后，对正态均值μ作出估计

3.对正态总体参数估计的描述正确的是( )。A．正态均值μ的无偏估计有两个，一个是样本均值的估计，另一个是样本中位数的估计，即μ(2＝Me＝(1/n)(X1+X2+…+Xn)B．对正态均值μ来说，样本均值总比样本中位数更有效，应舍去样本中位数C．在实际过程中，应优先选用样本均值去估计正态均值μ。但有时在现场，为了简便快捷，选用样本中位数去估计正态均值μ也是有的D．正态方差σ2的无偏估计常用的只有一个，就是样本方差S2

4.某样本数据在正态纸上描点,目测这些点在一直线附近,表示数据来自于正态总体,现从纵坐标轴上取概率为0.5,则其对应于近似直线上点的横坐标是正态总体________的估计。A．标准差σB．均值μC．μ+σD．μ+σ

更多“正态概率纸的作用有( )。A.判断一个样本是否来自正态总体B.若确定是正态分布,可估计正态均值与正 ”相关问题

  • 第1题：

    若一组数据服从正态分布，则下列判断正确的有( )。

    A．正态随机变量落入其均值左右各1个标准差内的概率是68．27％

    B．正态随机变量落入其均值左右各2个标准差内的概率是68．27％

    C．正态随机变量落入其均值左右各2个标准差内的概率是95．45％

    D．正态随机变量落入其均值左右各3个标准差内的概率是99．73％

    E．正态随机变量落入其均值左右各4个标准差内的概率是99．73％


    正确答案：ACD

  • 第2题：

    正态概率纸可以用来( )。A.估计正态分布的均值B.判断数据是否来自二项分布的总体SXB

    正态概率纸可以用来（ ）。

    A.估计正态分布的均值

    B.判断数据是否来自二项分布的总体

    C.估计正态分布的方差

    D.判断数据是否来自正态分布的总体

    E.估计正态分布的标准


    正确答案：ACDE
    ACDE。

  • 第3题：

    对正态总体参数的估计描述正确的是（ ）。

    A.正态均值μ的无偏估计有两个，一个是样本均值的估计，另一个是样本中位数的估计，即

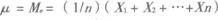
    B.对正态均值μ来说，样本均值总比样本中位数更有效，应舍去样本中位数

    C.在实际过程中，应优先选用样本均值去估计正态均值μ。但有时在现场，为了简便快捷，选用样本中位数去估计正态均值μ也是有的

    D.正态方差σ2的无偏估计常用的只有一个，就是样本方差S2

    E.正态方差σ2的无偏估计常用的只有一个，就是样本方差X2


    正确答案：CD

  • 第4题：

    某样本数据在正态纸上描点，目测这些点在一直线附近，表示数据来自于正态总体，现从纵坐标轴上取值为0.5，则其对应于近似直线上点的横坐标是正态总体( )的估计值。

    A.标准差σ

    B.均值μ

    C.μ+σ

    D.μ+2σ


    正确答案：B

  • 第5题：

    正态概率纸可以用来（ ）。
    A.估计正态分布的均值 B.判断数据是否来自二项分布的总体
    C.估计正态分布的方差 D.判断数据是否来自正态分布的总体
    E.估计正态分布的标准差


    答案：A,C,D,E
    解析：

  • 第6题：

    当正态总体方差已知时，在小样本情况下可以用正态分布对总体均值进行估计。（）


    正确答案:正确

  • 第7题：

    下列场合适合于用t统计量的是（）。

    • A、总体正态大样本方差未知
    • B、总体非正态大样本方差未知
    • C、总体正态小样本方差未知
    • D、总体非正态小样本方差未知

    正确答案:C

  • 第8题：

    作秩和检验要求资料（）

    • A、来自正态总体，方差齐性
    • B、来自正态总体，方差较小
    • C、来自严重偏态总体
    • D、来自正态总体，均数相差较大
    • E、以上都不要求

    正确答案:E

  • 第9题：

    正态概率纸的用处有（）

    • A、检验一个样本是否来自正态总体
    • B、若确定是正态分布，可估计正态均值和正态标准差
    • C、可用来检验一个样本是否来自对数正态分布   
    • D、用来检验一个样本是否来自二项分布

    正确答案:A,B,C

  • 第10题：

    多选题
    正态概率纸的作用有(　　)。
    A

    判断一个样本是否来自正态总体

    B

    若确定是正态分布，可估计正态均值与正态标准差

    C

    可用来检验一个样本是否来自对数正态总体

    D

    用来检验一个样本是否来自二项分布


    正确答案： C,A
    解析： 暂无解析

  • 第11题：

    多选题
    正态概率纸的用处有（）
    A

    检验一个样本是否来自正态总体

    B

    若确定是正态分布，可估计正态均值和正态标准差

    C

    可用来检验一个样本是否来自对数正态分布

    D

    用来检验一个样本是否来自二项分布


    正确答案： C,B
    解析： 暂无解析

  • 第12题：

    多选题
    正态概率纸可以用来（　　）。[2008年真题]
    A

    估计正态分布的均值

    B

    判断数据是否来自二项分布的总体

    C

    估计正态分布的方差

    D

    判断数据是否来自正态分布的总体

    E

    估计正态分布的标准差


    正确答案： E,D
    解析： 正态概率纸的作用有:①检验一组数据（即样本）x1，x2，…，xn是否来自正态分布；②在确认样本来自正态分布后，可在正态概率纸上作出正态均值μ与正态标准差σ的估计；③在确认样本来自非正态分布后，可对数据作变换后再在正态概率纸上描点，若诸点近似在一直线附近，则可认为变换后的数据来自某正态总体。

  • 第13题：

    正态概率纸的作用有（ ）。

    A.检验一个样本是否来自正态分布

    B.检验一个样本是否来自二项分布

    C.检验一个样本是否来自对数正态分布

    D.若描点呈直线状，可在图上作正态均值肚的估计

    E.若描点呈直线状，可在图上作正态标准差仃的估计


    正确答案：ACDE
    ACDE。

  • 第14题：

    以下情况可以用Z统计量检验的有( )。

    A总体均值的检验，小样本

    B正态总体均值的检验，小样本，方差未知

    C大样本总体均值的检验

    D正态总体方差的检验


    参考答案D

  • 第15题：

    正态分布N(μ，ó2)中ó的含义及性质为（ ）。

    A.正态方差

    B.ó越小。分布越集中

    C.正态标准差

    D.ó越大，分布越分散

    E.正态均值


    正确答案：BCD
    BCD。

  • 第16题：

    正态概率纸可以用来（ ）。[2008年真题]
    A.估计正态分布的均值 B.判断数据是否来自二项分布的总体
    C.估计正态分布的方差 D.判断数据是否来自正态分布的总体
    E.估计正态分布的标准差


    答案：A,D,E
    解析：
    正态概率纸的作用有：①检验一组数据（即样本）x1，x2…，xn是否来自正态分布；②在确认样本来自正态分布后，可在正态概率纸上作出正态均值μ与正态标准差σ的估计；③在确认样本来自非正态分布后，可对数据作变换后再在正态概率纸上描点，若诸点近似在一直线附近，则可认为变换后的数据来自某正态总体。

  • 第17题：

    正态概率纸的作用有（ ）。
    A.检验一个样本是否来自正态分布 B.检验一个样本是否来自二项分布
    C.检验一个样本是否来自对数正态分布
    D.若描点呈直线状，可在图上作正态均值μ的估计
    E.若描点呈直线状，可在图上作正态标准差σ的估计


    答案：A,C,D,E
    解析：

  • 第18题：

    当样本容量足够大时，允许我们使用正态概率分布来近似样本均值和样本成数的抽样分布，这种定理是（）。

    • A、近似定理
    • B、正态概率定理
    • C、中心极限定理
    • D、中心正态定理

    正确答案:C

  • 第19题：

    以下问题可以用Z检验的有（）。

    • A、正态总体均值的检验，方差已知
    • B、正态总体均值的检验，方差未知
    • C、大样本下总体均值的检验
    • D、正态总体方差的检验

    正确答案:A,C

  • 第20题：

    对于正偏态分布的总体，当样本含量足够大时，样本均数的分布近似为（）

    • A、正偏态分布
    • B、负偏态分布
    • C、正态分布
    • D、t分布

    正确答案:C

  • 第21题：

    若一组数据服从正态分布，则下列判断正确的有（）。

    • A、正态随机变量落入其均值左右各1个标准差内的概率是68.27%
    • B、正态随机变量落入其均值左右各2个标准差内的概率是68.27%
    • C、正态随机变量落入其均值左右各2个标准差内的概率是95.45%
    • D、正态随机变量落入其均值左右各3个标准差内的概率是99.73%
    • E、正态随机变量落入其均值左右各4个标准差内的概率是99.73%

    正确答案:A,C,D

  • 第22题：

    单选题
    某样本数据在正态纸上描点，目测这些点在一直线附近，表示数据来自于正态总体，现从纵坐标轴上取值为0．5,则其对应于近似直线上点的横坐标是正态总体(　　)的估计值。
    A

    标准差σ  

    B

    均值μ  

    C

    μ＋σ  

    D

    μ＋2σ


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    某样本数据在正态纸上描点，目测这些点在一直线附近，表示数据来自于正态总体，现从纵坐标轴上取概率为0.5，则其对应于近似直线上点的横坐标是正态总体（　　）的估计。
    A

    标准差 σ

    B

    均值 μ

    C

    μ+σ

    D

    μ－σ


    正确答案： C
    解析： 正态分布的均值是其分布的中心位置，概率密度函数曲线下的面积的一半为0.5，所以在正态概率纸上概率为0.5处对应的就是均值μ的估计值。

相关内容