在一元线性回归中,给出n对数据(xi,yi),i=1,2,…,n,若其回归方程为bx,则下述结论成立的有( )。A.总离差平方和ST=LyyB.回归平方和SR=bLxyC.残差平方和SE=ST-SR)D.残差平方和的自由度为n-1E.残差平方和Se=ST-Sf
题目
在一元线性回归中,给出n对数据(xi,yi),i=1,2,…,n,若其回归方程为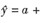 bx,则下述结论成立的有( )。
bx,则下述结论成立的有( )。
A.总离差平方和ST=Lyy
B.回归平方和SR=bLxy
C.残差平方和SE=ST-SR)
D.残差平方和的自由度为n-1
E.残差平方和Se=ST-Sf
相似考题
更多“ 在一元线性回归中,给出n对数据(xi,yi),i=1,2,…,n,若其回归方程为bx,则下述结论成立的有( )。A.总离差平方和ST=LyyB.回归平方和SR=bLxyC.残差平方和SE=ST-SR)D.残差平方”相关问题
-
第1题:
在一元线性回归的总偏差平方和的表达式中,结论正确的是( )。
A.总偏差平方和ST的自由度为n-1
B.回归平方和SR的自由度为n-2
C.残差平方和的自由度为1
D.SE=ST-SR
E.残差平方和的自由度为n-2
正确答案:ADE
解析:一元线性回归的总偏差平方和的表达式中,回归平方和SR的自由度fR=1(相应于自变量的个数);总偏差平方和ST的自由度为n-1;残差平方和的自由度为fE=fy-fR,故fE=n-2。 -
第2题:
若收集了n组数据(xi,yi),i=1,2,…,n,并求得Lxx=330,Lxy=168,如Lyy= 88.9,则一元线性回归方程(作图)中的b=( )。
A.0.5091
B.0.5292
C.1.8898
D.1.9643
正确答案:A
解析: -
第3题:
在一元线性回归分析中,根据数据(xi,yi),已知:Lxx=10, Lxy=8,以下计算正确的有 ( )。
A.总平方和ST= 5. 5 B.回归平方和SR =6.4
C. r = 1. 25 D.b=0. 8
E.残差平方和SE=7答案:B,D解析:回归方程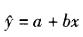 ,b = Lxy/Lxx = 0. 8 ;回归平方和SR=bLxy=6. 4。
,b = Lxy/Lxx = 0. 8 ;回归平方和SR=bLxy=6. 4。 -
第4题:
收集了n组数据(xi,yi), i =1, 2,…n,在一元线性回归中用SR表示回归平方和, SE表示残差平方和,由此求得F比,则当( )时在显著性水平a上认为所得到的回归方程是有意义的。
A. F>F1-a(1, n) B. F>F1-a(1, n-1)C. F>F1-a(1, n-2) D. F1-a(1, n-2)答案:C解析:由于fR =1,fE =fT-fR =n-1-1= n -2,所以在显著性水平a上,当F>F1-a(1, n-2) 时认为所得到的回归方程是有意义的。 -
第5题:
根据15对数据(x1,y1),i=1,2,…,15,建立一元线性回归方程,则残差平方和的自由度为( )。
A. 1 B. 2 C. 13 D. 14答案:C解析:ST、SA 、Se的自由度分别用fT、fA、fe表示,其有分解式:fT=n-1=15-1=14,fA =1,fe=fT -fA =14-1= 13。 -
第6题:
根据18对观测值(xi,yi),i=1,2,…,18,建立了一光线性回归方程。在对该回归方程作显著性检验时,其回归平方和的自由度fR与残差平方和的自由度fE分别为( )
A.fR=1
B.fR= 2
C.fE=18
D.fE=17
E.fE=16答案:A,E解析:。fE=n-2=18-2=16 -
第7题:
用 F 检验考查一元线性回归方程的有效性时,总平方和可以被分解为()A.残差平方和、区组平方和
B.回归平方和、残差平方和
C.残差平方和、组间平方和、区组平方和
D.回归平方和、系统误差平方和、残差平方和答案:B解析: -
第8题:
根据方差分析原理,将y的n个观察值之间的差异,用观察值yi与其平均值y的离差平方和来表示,并称之为()
- A、总离差平方和
- B、回归平方和
- C、残差平方和
正确答案:A -
第9题:
用于检验线性回归方程可信度的统计量F等于()。
- A、回归平方和除以残差平方和
- B、残差平方和除以回归平方和
- C、平均回归平方和除以平均残差平方和
- D、平均残差平方和除以平均回归平方和
正确答案:C -
第10题:
多选题在一元线性回归的总偏差平方和的表达式中,结论正确的是( )。A总偏差平方和ST的自由度为n-1
B回归平方和SR的自由度为n-2
C残差平方和的自由度为1
DSE=ST-SR
E残差平方和的自由度为n-2
正确答案: B,A解析:
一元线性回归的总偏差平方和的表达式中,回归平方和SR的自由度fR=1(相应于自变量的个数);总偏差平方和ST的自由度为n-1;残差平方和的自由度为:fE=fT-fR,故fE=n-2。 -
第11题:
单选题对模型Yi=β0+β1X1i+β2X2i+mi的最小二乘回归结果显示,R2为0.92,总离差平方和为500,则残差平方和RSS为( )。A10
B40
C80
D20
正确答案: B解析:
由R2=ESS/TSS=1-RSS/TSS,即0.92=1-RSS/500,解得:RSS=40。 -
第12题:
单选题根据方差分析原理,将y的n个观察值之间的差异,用观察值yi与其平均值y的离差平方和来表示,并称之为()A总离差平方和
B回归平方和
C残差平方和
正确答案: B解析: 暂无解析 -
第13题:
在一元线性回归中,给出n对数据(xi,yi),i=1,2…,n,若其回归方程为,则下述结论成立的有( )。
A.总偏差平方和ST=Lyy
B.归平方和SR=bLxy
C.残差平方和Se=ST-SR
D.残差平方和的自由度为n-1
E.残差平方和Se=ST-Sf
正确答案:ABC
-
第14题:
在一元线性回归的总偏差平方和的表达式中,结论正确的是( )。A.总偏差平方和ST的自由度为n-1 B.回归平方和SR的自由度为n-2
C.残差平方和的自由度为1 D. SE=ST-SR
E.残差平方和的自由度为n-2答案:A,D,E解析:一元线性回归的总偏差平方和的表达式中,回归平方和SR的自由度fR= 1 (相应于自变量的个数);总偏差平方和ST的自由度为n-1;残差平方和的自由度为:fE=fT-fR,故fE=n-2。 -
第15题:
根据20对数据(xi,yi), i=1, 2,…,20,建立一元线性同归方程,则残差平方和的自由度为( )。
A. 1 B. 2
C. 18 D.19答案:C解析:。残差平方和的自由度为n-2。 -
第16题:
在一元线性回归中,给出n对数据(xi,yi), i =1, 2,…n,若其回归方程为 ,则下述结论成立的有( )。A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxy
,则下述结论成立的有( )。A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxy
C.残差平方和SE=ST-SR D.残差平方和的自由度为n-1
E.残差平方和Se=ST-Sf答案:A,B,C解析:残差平方和的自由度为fE=n-2。 -
第17题:
在一元线性回归中,给出n对数据(xi,yi), i =1, 2,…n,若其回归方程为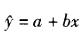 ,则下述结论不成立的有( )。
,则下述结论不成立的有( )。
A.总偏差平方和ST=Lyy B.回归平方和SR=bxLxy
C.残差平方和SE=ST-SR D.残差平方和的自由度为n-1答案:D解析:总偏差平方和的自由度fT=n-1,回归平方和的自由度fR =1,所以残差平方和的自由度fE =fT-fR = n -2。 -
第18题:
在k元回归中,n为样本容量,SSE为残差平方和,SSR为回归平方和,则对回归方程线性关系的显著性进行检验时构造的F统计量为()。
 答案:C解析:对回归方程线性关系的显著性进行检验的步骤为:
答案:C解析:对回归方程线性关系的显著性进行检验的步骤为:
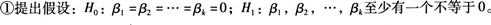
②计算检验的统计量F:
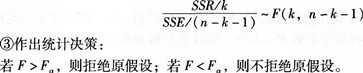
-
第19题:
下列关于回归平方和的说法,正确的有( )。
Ⅰ 总的离差平方和与残差平方和之差
Ⅱ 无法用回归直线解释的离差平方和
Ⅲ 回归值与均值的离差平方和
Ⅳ 实际值与均值的离差平方和A.Ⅰ、Ⅱ
B.Ⅰ、Ⅲ
C.Ⅰ、Ⅳ
D.Ⅱ、Ⅲ答案:B解析:Ⅱ项,回归平方和是可用回归直线解释的离差平方和;Ⅳ项为总离差平方和。 -
第20题:
一元线性回归模型Yi=β0+β1Xi+μi的最小二乘回归结果显示,残差平方和RSS=40.32,样本容量n=25,则回归模型的标准差σ为()。
- A、1.270
- B、1.324
- C、1.613
- D、1.753
正确答案:B -
第21题:
相关系数的计算公式是()。
- A、残差平方和除以总离差
- B、残差平方和除以总离差,再开平方根
- C、回归平方和除以总离差
- D、回归平方和除以总离差,再开平方根
正确答案:B -
第22题:
单选题根据15对数据(x1,y1),i=1,2,…,15,建立一元线性回归方程,则残差平方和的自由度为( )。[2010年真题]A1
B2
C13
D14
正确答案: B解析:
ST、SA、Se的自由度分别用fT、fA、fe表示,则:fT=n-1=15-1=14,fA=1,fe=fT-fA=14-1=13。 -
第23题:
单选题对模型yi=β0+β1x1i+β2x2i+μi的最小二乘回归结果显示,R2为0.92,总离差平方和为500,则残差平方和RSS为( )。A10
B40
C80
D20
正确答案: B解析:
根据题意,总离差平方和TSS=500,根据公式R2=1-RSS/TSS=0.92,解得:RSS=40。
