抛三枚硬币，记A=“恰有一个正面出现”，则P(A)=( )。A．1/8B．1/6C．1/3D．3/8

题目

抛三枚硬币，记A=“恰有一个正面出现”，则P(A)=( )。

A．1/8

B．1/6

C．1/3

D．3/8

相似考题

1.抛三枚硬币，记A＝“恰有一个正面出现”，则P(A)＝( )。A．1/3B．1/6C．3/8D．1/8

2.标准液的效期为()月。A.1～2B.2～6C.1～3D.3～6

3.连抛一枚均匀硬币4次,既有正面又有反面的概率为________。A．7/8B．1/8C．5/8D．1/16

4.连抛一枚均匀硬币4次，既有正面又有反面的概率为( )。A．1/16B．1/8C．5/8D．7/8

更多“抛三枚硬币,记A=“恰有一个正面出现”,则P(A)=()。A.1／8B.1／6C.1／3D.3／8 ”相关问题

  • 第1题：

    小明和小芳做抛硬币的游戏（硬币是均匀的）。

    （1）小明前三次抛的结果都是正面朝上，第四次一定会是正面朝上吗？

    （2） 小芳抛10次硬币，一定是5次正面朝上、5次反面朝上吗？你怎么看以上两个问题，与同伴交流。


    （1）第4次可能正面朝上，也可能反面朝上。

    （2）不一定5次正面朝上，5次反面朝上。

  • 第2题：

    投掷一枚硬币5次，记其中正面向上的次数为X，则P{X≦4}=31/32。()


    正确答案:对

  • 第3题：

    早产儿鼻管喂养减量的依据是残留奶占前次奶量的

    A．1／8

    B．1／6

    C．1／5

    D．1／4

    E．1／3


    正确答案：E

  • 第4题：

    一个抛硬币的游戏，规则为：支付5元获得一次抛硬币的机会，如出现正面则可获得20元，若出现反面则需额外支付12元。一个游戏参与者抛一次硬币获得收益的数学期望为()元。

    A:8
    B:4
    C:3
    D:-1

    答案：D
    解析：
    本题考查的是数学期望的计算。一次游戏获得收益的数学期望=20*50%+（-12）*50%-5=-1（元）。

  • 第5题：

    过长方体一侧面的两条对角线交点，与下底面四个顶点连得一四棱锥，则四棱锥与长方体的体积比为多少？


    A.1:8
    B.1:6
    C.1:4
    D.1:3

    答案：B
    解析：
    设正方体的边长为1,则其体积为1。如图所示，此四棱锥的高为1/2，体积=1/3Sh=1/3×12×1/2=1/6。所以二者体积比为1:6。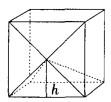

  • 第6题：

    一枚硬币抛三次，恰好出现两次正面的概率是多少？()

    A.1/8
    B.3/8
    C.1/4
    D.1/2

    答案：B
    解析：
    推断统计；推断统计的数学基础。 一枚硬币抛掷三次可能出现的结果共8种，每种结果出现的可能为1／8，出现两次正面的情况有3种，故而两次正面的概率为3/8。

  • 第7题：

    全脂奶粉按重量调配，奶粉与水的比例是

    A.1:8
    B.1:6
    C.1:4
    D.4:1
    E.2:1

    答案：A
    解析：
    全脂奶粉按重量调配，奶粉与水的比例是1:8；按容积调配，奶粉与水的比例是1:4。

  • 第8题：

    连抛一枚均匀硬币4次，既有正面又有反面的概率为（ ）。
    A. 1/16 B. 1/8 C. 5/8 D. 7/8


    答案：D
    解析：
    连抛硬币4次可重复排列数为：n=24= 16。而全是正面或全是反面各1种可能，所以既有正面又有反面的有：k = 16－2 =14种可能。故“既有正面又有反面”的概率为：P（A） =k/n=7/8。

  • 第9题：

    抛一个质量均匀的硬币100次，其中52次正面朝上，再抛100次，其中46次正面朝上，这说明随即事件的规律性中也表现出某种随机性。


    正确答案:正确

  • 第10题：

    抛一个质量均匀的硬币，其正面向上的概率为1/2，因此在抛这个硬币100次时，不可能出现没有正面向上的情况。


    正确答案:错误

  • 第11题：

    单选题
    抛3枚硬币，出现3次正面的概率为()。
    A

    0.12

    B

    0.15

    C

    0.25

    D

    0.125


    正确答案： B
    解析： 抛3枚硬币一共会出现8种结果，全为正面是其中的一种，概率为1÷8=0.125

  • 第12题：

    单选题
    抛三枚硬币，记A=“恰有一个正面出现”，则P（A）=（　　）。
    A

    1/8

    B

    1/6

    C

    1/3

    D

    3/8


    正确答案： D
    解析：
    样本点共有23=8，其中恰有一个正面出现的样本点为3个，故P（A）=3/8。

  • 第13题：

    小张通过某种数学考试的概率是1/2,他连续测试三次,那么其中恰有一次获得通过的概率为________。

    A．1/8

    B．1/4

    C．3/8

    D．1/2


    正确答案：C
    解析：由于共有n=23=8种可能考试结果,并考试次数k为3,所以P=k/n=3/8。

  • 第14题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第15题：

    如下事件发生的概率等于1/4的是()。

    A:抛两枚普通的硬币，出现的均是正面
    B:一个不透明的袋子里装着黑白红蓝四种颜色的球，随机拿出一个恰好为红色球
    C:抛两枚普通的硬币，出现一个正面和一个反面
    D:掷一枚普通的骰子，出现点数小于3
    E:掷两枚普通的骰子，出现点数之和小于

    答案：A,B
    解析：
    A选项，出现两个都是正面的概率=1/2*1/2=1/4；B选项，考查古典概率计算方法的使用，随机拿出一个球可能有4种颜色，红色只占其中一种，所以拿出恰为红色球的概率=1/4；C选项，出现一个正面和一个反面应该包括两种情况：正反、反正，因此其概率=1/4+1/4=1/2；D选项，掷出的点数总共有6种情况，而小于3的只有l和2两种情况，所以其概率=2/6=1/3；E选项，掷两枚骰子，出现的点数和最小为2，即两枚骰子的点数都是1，因此其和小于2是不可能事件，所以概率=0。

  • 第16题：

    抛三枚硬币，记A= “恰有一个正面出现”，则=( )。
    A. 1/8 B. 1/6 C. 1/3 D.3/8


    答案：D
    解析：
    样本点共有23 =8，其中恰有一个正面出现的样本点为3个，故P(A)=3/8。

  • 第17题：

    过正方体一侧面的两条对角线交点，与下底面四个顶点连得一四棱锥，则四棱锥与正方体的体积比是多少？（）

    A.1：8
    B.1：6
    C.1：4
    D.1：3

    答案：B
    解析：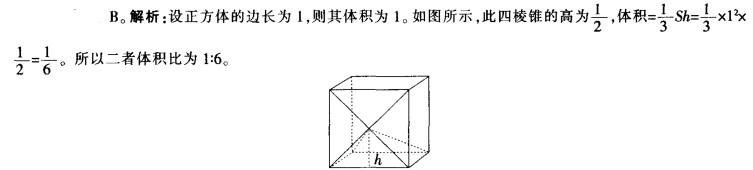
    。

  • 第18题：

    二级医院高、中、初级的比例是

    A.1：3：8
    B.1：3：6
    C.1：2：8～9
    D.1：2：6
    E.2：3：6

    答案：A
    解析：
    医院高级、中级、初级员工的比例：一级医院为1：2：8～9；二级医院为1：3：8；三级医院为1：3：6。

  • 第19题：

    同时抛掷三枚质地完全相同的硬币，则正面与反面都出现的概率为（ ）。

    A.1/4
    B.1/3
    C.2/3
    D.3/4

    答案：D
    解析：

  • 第20题：

    同时掷3枚均匀硬币，则恰有2枚正面朝上的概率为（）.

    • A、0.5
    • B、0.25
    • C、0.125
    • D、0.375

    正确答案:D

  • 第21题：

    抛3枚硬币，出现3次正面的概率为（）。

    • A、0.12
    • B、0.15
    • C、0.25
    • D、0.125

    正确答案:D

  • 第22题：

    单选题
    抛三枚硬币，至少出现一个正面的概率为 (　　)。
    A

    1/4

    B

    1/8

    C

    3/8

    D

    7/8


    正确答案： B
    解析： 暂无解析

  • 第23题：

    判断题
    抛一个质量均匀的硬币，其正面向上的概率为1/2，因此在抛这个硬币100次时，不可能出现没有正面向上的情况。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容