由 10 对观测值 (xi,yi),i=1，2,…，10，计算得Lxx= 160，Lxy=－216，Lyy =﹣360,则样本相关系数r=( )。 A. 0. 90 B. 0. 85 C. ﹣0. 85 D. ﹣0. 90
题目
A. 0. 90 B. 0. 85
C. ﹣0. 85 D. ﹣0. 90
相似考题
更多“由 10 对观测值 (xi,yi),i=1，2,…，10，计算得Lxx= 160，Lxy=－216，Lyy =﹣360,则样本相关系数r=( )。 ”相关问题
-
第1题：
设r为由n对数据(xi，yi)算出的相关系数，y=a+bx为相应的一元回归方程，则（ ）。
A.r与b同号
B.r与b异号
C.b与Lxy同号
D.b与Lxy异号
E.r与Lxy异号
正确答案：AC
r、b、Lxy同号。 -
第2题：
两个变量(x，y)，其观测值为(xi，yi，i=1，2，…，n。若显著性水平为a，简单相关系数为 r，则下列说法正确的有（ ）。
A.-1≤r≤1
B.r=0，x、y之间存性相关
C.r=-1，完全负线性相关
D.相关系数检验的临界值表示为
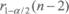
E.r=0，x、y之间不存性相关
正确答案：ACDE
r=0时称两个变量之间线性不相关。 -
第3题：
由n个数组(xi，yi。)计算得 Lxx=330，Lxy=-l68，Lyy=9.4 由此可以看出（ ）。
A.x与y，的相关系数r>0
B.x与Y的相关系r<0
C.Y对x的回归系数b>0
D.y对x的回归系数b>0
E.相关系数r与回归系数异号
正确答案：BD
BD。 -
第4题：
两个变量(x，y)，其观测值为(xi，yi)，i=1，2，……，n。当相关系数的绝对值|r|大于某个临界值时，就认为它们之间存在一定的线性相关关系。若给定显著水平a，则临界值为（ ）。
A.
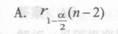
B.
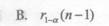
C.
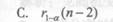
D.
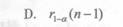正确答案：A
-
第5题：
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：
，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
回归方程中的常数项a为（ ）。
A. -19.6 B. -2.6 C. 2.6 D. 26答案：C解析：
-
第6题：
由n个数组（xi，yi)计算得Lxx= 330，_Lxy=﹣168，Lyy= 9.4由此可以看出（ ）。
A. x与y的相关系数r>0
B.工与y的相关系数r
C. y对x的回归系数b>0
D. y对x的冋归系数b
E.相关系数r与回归系数b异号答案：B,D解析：
-
第7题：
若r是由n对观测值（xi，yi)计算得到的x，y的相关系数，y = a + bx表示相 应的回归方程，则下列说法中，正确的有（ ）。
A.若 r= 1，则 b= 1
B.若 r=﹣1，则 b＜0
C.若r≠0，则/b≠0
D. r与b同号
E. r与a异号答案：B,C,D解析： -
第8题：
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：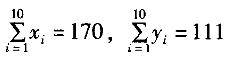
，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
Y对X的回归系数b为（ ）。
A. 0.5 B. -0.5 C. 0.582 D. -0.582答案：A解析：设一元线性回归方程的表达式为：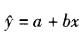
。则根据公式，b=Lxy/Lxx，
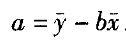，求得：b=Lxy/Lxx=168/336 =0.5。 -
第9题：
由合金碳含量(％)与合金强度（107Pa）的12对观测值(xi,yi), i =1， 2，…12，计算得到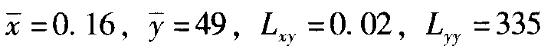
，则计算结果正确的有（ ）。
A. r=0. 94 B. b=0.007 C. a =29. 56 D. fE=11
E.总离差平方和ST= 0.02答案：A,C解析：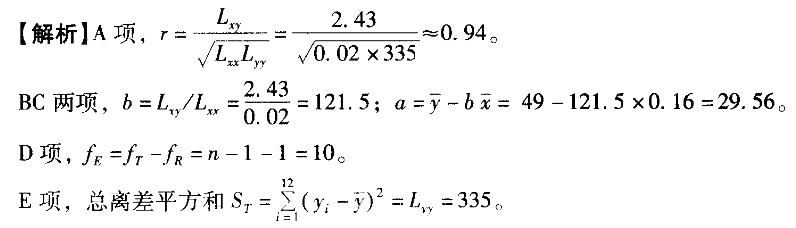
-
第10题：
由 12 对数据 （xi，yi）,i = 1，2,…，12，算得 Lxx=165，Lyy=372, Lxy=﹣232，则X与Y间的相关系数r为（ ）。
A. 0. 936 B. ﹣0. 936
C. 0.875 D. ﹣0. 875答案：B解析：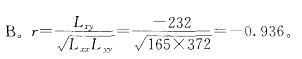
-
第11题：
由n个数组(xi,yi)计算得Lxx= 330, Lxy =-168,Lxy=9.4由此可以看出（）。
A. X与y，的相关系数r>0
B. X与y的相关系数rC. y与x对r的回归系数b>0
D. y对x的回归系数bE.相关系数r与回归系数异号答案：B,D解析： -
第12题：
单选题相关系数是计算公式是（）Ar=Lxx/∫LxyLyy
Br=Lyy/∫LxxLxy
Cr=Lxy/∫LxxLyy
Dr=∫LxyLyy
正确答案： C解析： 暂无解析 -
第13题：
两个变量(x，y)，其观测值为(xi，yi)，i=1，2，…，n。则简单相关系数r的表达式不正确的是( )。
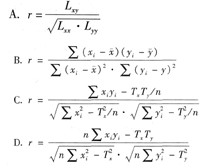
A．
B．
C．
D．
正确答案：B
解析：B项应为 -
第14题：
由l5对数据(xi，yi)，i=1，2，…，15，算得Lxx=355，Lyy=3102，Lxy=－923，贝0回归方程y=a+bx中回归系数b=（ ）。
A.1.7
B.－l.7
C.2.6
D.－2.6
正确答案：D
D。 -
第15题：
若收集了n组数据(xi，yi)，i=1，2，…，n，并求得Lxx=330，Lxy=168，如Lyy= 88.9，则一元线性回归方程(作图)中的b=( )。
A．0.5091
B．0.5292
C．1.8898
D．1.9643
正确答案：A
解析： -
第16题：
若收集了n组数据(xi,yi), i =1， 2，…n，并求得Lxx=330，Lxy=168，Lyy=88.9，则一元线性回归方程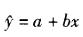
中的b=( )。
A. 0.5091 B. 0.5292 C. 1. 8898 D. 1.9643答案：A解析：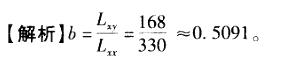
-
第17题：
由 10 对观测值（xi，yi)，i＝1，…，10，求得 Lxx＝196，Lyy＝144，Lxy＝142，则下列计算结果中，正确的有（ ）。
A.相关系数为0. 845 2 B.相关系数为0. 724 5
C.相关系数为﹣0.845 2 D. y对的回归系数为0. 9861
E. y对x的回归系数为0.724 5答案：A,E解析：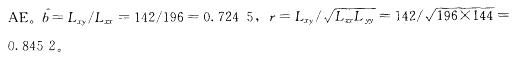
-
第18题：
两个变量(xi，yi)，其观测值为(xi,yi), 则简单相关系数r的表达式不正确的是（ ）。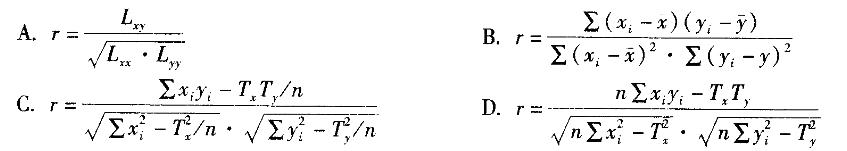
答案：B解析：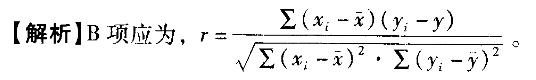
-
第19题：
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：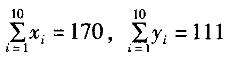
，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
X与Y的样本相关系数r为（ ）。
A. -0.8 B. 0.8 C. 0.64 D. 0.5答案：B解析：相关系数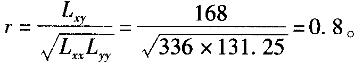
-
第20题：
设两变量X与Y的观测值为(xi,yi)，i= 1，2，…，n,用r表示相关系数，y = a + bc表示回归方程，以下结论正确的有（ ）。
A.若 r=1，则b=1 B.若 rC.若 r=0，则b= 0 D.若r>0，则b>0
E.若 r = 1，则 a = 0答案：B,C,D解析： -
第21题：
由 15 对数据（xi，yi),= 1, 2，…，15，算得 Lxx= 355，Lyy = 3102, Lxy =— 923，则回归方程
中回归系数b=( )。
A. 1.7 B. —1.7
C. 2. 6 D. —2. 6答案：D解析：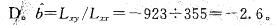
-
第22题：
两个变量(x, y),其观测值为（xi, yi) i= l, 2,…，n。则简单相关系数r的表达式不正确的是（ ）。
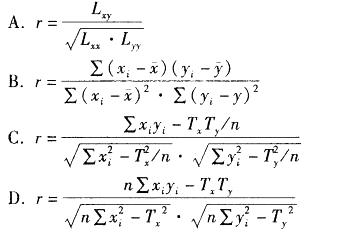答案：B解析：
-
第23题：
相关系数是计算公式是（）
- A、r=Lxx/∫LxyLyy
- B、r=Lyy/∫LxxLxy
- C、r=Lxy/∫LxxLyy
- D、r=∫LxyLyy
正确答案:C