假设某总体服从正态分布N(12，4)，现从中随机抽取一容量为5的样本X1，X2，X3，X4，X5，则：样本均值与总体均值之差的绝对值大于1的概率是( )。A．0.2628B．0.98C．0.9877D．0.9977

题目

假设某总体服从正态分布N(12，4)，现从中随机抽取一容量为5的样本X1，X2，X3，X4，X5，则：

样本均值与总体均值之差的绝对值大于1的概率是( )。

A．0.2628

B．0.98

C．0.9877

D．0.9977

相似考题

1.一组样本数据为x1=10.0，x2=10.1，x3=9.8，x4=10.2，x5=9.9，则该样本组平均值与极差为（ ）。A．10.0，0.2B．0，0.4C．10.0，0D．10.0，0.4

2.假设某总体服从正态分布N(12, 4)，现从中随机抽取一容量为5的样本X1,X2, X3, X4, X5，则： 概率P{max(X1,X2, X3, X4, X5) >15)=( )。 A. 0.2533 B. 0. 2893 C. 0.2923 D. 0.2934

3.假设某总体服从正态分布N(12, 4)，现从中随机抽取一容量为5的样本X1,X2, X3, X4, X5，则： 样本均值与总体均值之差的绝对值大于1的概率是（）。 A. 0.2628 B. 0. 98 C. 0.9877 D. 0.9977

4.样本X1,X2,X3,X4取自正态分布总体X,EX=μ为已知,而DX=б2未知,则下列随机变量中不能作为统计量的是()

更多“假设某总体服从正态分布N(12,4),现从中随机抽取一容量为5的样本X1,X2,X3,X4,X5,则: 样本均值与总 ”相关问题

  • 第1题：

    设总体X～N（μ,25）,X1,X2,…,X100为来自总体的简单随机样本,求样本均值与总体均值之差不超过1.5的概率


    答案：
    解析：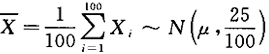
    总体均值为E(X)=μ，
    则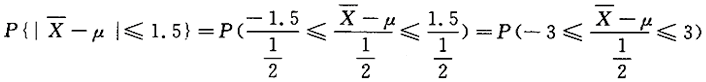
    =Ф(3)-Ф（-3）=2Ф(3)-1=0.9973

  • 第2题：

    设总体服从正态分布，总体方差未知，现抽取一容量为15的样本，拟对总体均值进行假设检验，检验统计量是（ ）。



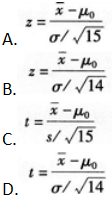    答案：C
    解析：
    在小样本情况下：总体服从正态分布，总体方差已知时，对总体均值进行假设

  • 第3题：

    假设总体服从正态分布，从该总体中抽取容量为12的样本，则样本均值的抽样分布（）

    A．服从非正态分布

    B．服从正态分布

    C．服从均匀分布

    D．服从t分布


    服从正态分布

  • 第4题：

    设总体X服从正态分布N(μ，σ^2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，Xn(n≥2)，其样本均值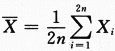,求统计量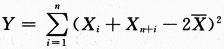的数学期望E(Y).


    答案：
    解析：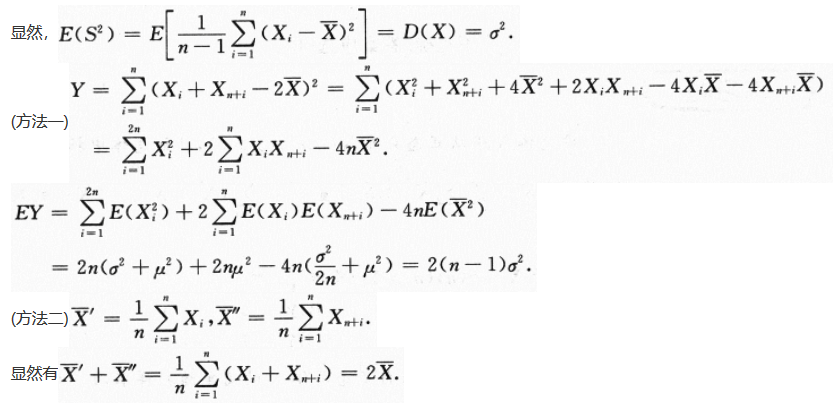

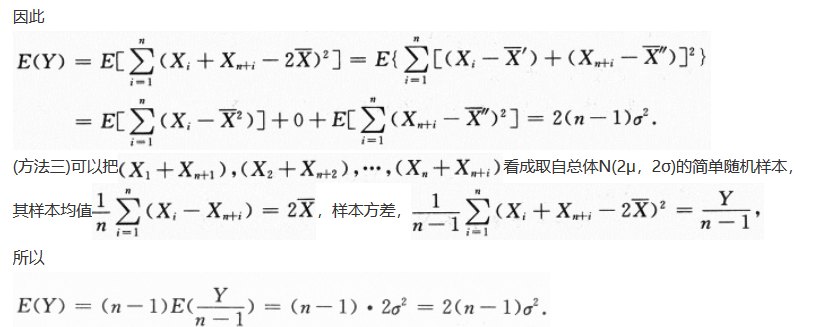
  • 第5题：

    从某总体中随机抽出5个样本，观测值分别为x1，x2，x3 ，x4，X5，从小到大依次排列为x1，x5，x4，x3，X2，则均值、极差和中位数分别为（ ）。



    答案：B
    解析：

相关内容