关于正态均值μ的假设检验(σ已知情形)常用的三对假设为( )。 A. H0:μ≤μ0 , H1:μ>μ0 B. H0:μ≥μ0 , H1:μ0 C. H0:μ=μ0 , H1:μ≠μ0 D. H0:μ≤μ0 , H1:μ0 E. H0:μ≥μ0 , H1:μ>μ0
题目
A. H0:μ≤μ0 , H1:μ>μ0 B. H0:μ≥μ0 , H1:μ0
C. H0:μ=μ0 , H1:μ≠μ0 D. H0:μ≤μ0 , H1:μ0 E. H0:μ≥μ0 , H1:μ>μ0
相似考题
更多“关于正态均值μ的假设检验(σ已知情形)常用的三对假设为( )。 ”相关问题
-
第1题:
对正态总体参数的估计描述正确的是( )。
A.正态均值μ的无偏估计有两个,一个是样本均值的估计,另一个是样本中位数的估计,即
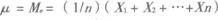
B.对正态均值μ来说,样本均值总比样本中位数更有效,应舍去样本中位数
C.在实际过程中,应优先选用样本均值去估计正态均值μ。但有时在现场,为了简便快捷,选用样本中位数去估计正态均值μ也是有的
D.正态方差σ2的无偏估计常用的只有一个,就是样本方差S2
E.正态方差σ2的无偏估计常用的只有一个,就是样本方差X2
正确答案:CD
-
第2题:
在假设检验中,方差已知的正态总体均值的检验要计算Z统计量。()
答案:(错)
-
第3题:
假设检验的Ⅱ类错误是()A.原假设为真而被接受
B.原假设为真而被拒绝
C.原假设是假而被接受
D.原假设是假而被拒绝答案:C解析:推断统计;假设检验。 在假设检验中虚无假设本来是正确的但被拒绝了,这类错误被称为弃真错误,即I型错误,又称α错误;虚无假设本来不正确但却接受了,这类错误称为取伪错误,即Ⅱ类错误,又称口错误。Ⅱ类错误是又叫纳伪错误,意思就是原假设为假却被错误地接受了。所以选择C。 -
第4题:
假设检验的Ⅱ类错误是( )A.原假设为真而被接受
B.原假设为真而被拒绝
C.原假设为假而被接受
D.原假设为假而被拒绝答案:C解析:本题旨在考查考生对Ⅱ类错误的正确理解和把握。Ⅱ类错误是指在接受为真时所犯的错,这类错误也称为β错误。也就是说.接受
时并不等于说二者100%的没有差异,同样有犯错误的可能性。故本题的正确答案是C
-
第5题:
当正态总体方差已知时,在小样本情况下可以用正态分布对总体均值进行估计。()
正确答案:正确 -
第6题:
在大样本情况下,对方差已知的非正态总体的均值进行区间估计或假设检验使用的统计量是()
- A、正态统计量
- B、X2统计量
- C、T统计量
- D、F统计量
正确答案:A -
第7题:
当均值大于众数时称为正偏态
正确答案:正确 -
第8题:
以下问题可以用Z检验的有()。
- A、正态总体均值的检验,方差已知
- B、正态总体均值的检验,方差未知
- C、大样本下总体均值的检验
- D、正态总体方差的检验
正确答案:A,C -
第9题:
以下关于正态分配的叙述错误的是()
- A、是重要的连续数据分配
- B、平均数和极差决定了正态分配曲线
- C、曲线为钟型左右对称
- D、均值和中位数相等
正确答案:B -
第10题:
单选题μ代表的是()A正态总体均值,表示数据分布的中心位置
B数据的平均值
C正态总体标准差,表示数据分布的离散程度
D数据的极差
正确答案: A解析: 暂无解析 -
第11题:
多选题下列关于t检验法的说法中,正确的是()。A进行检验的资料必须代表各连续变量
B主要运用于正态总体均值的检验和两个正态总体的均值之差的检验
C是一种非参数统计方法
D总体方差未知,正态总体均值的检验公式。
正确答案: A,C解析: 暂无解析 -
第12题:
单选题当总体为正态总体,方差已知,样本量为40,此时进行均值检验,应采用()统计量进行检验。A卡方
Bt
CF
DZ
正确答案: A解析: 暂无解析 -
第13题:
当总体为正态总体,方差已知,样本量为40,此时进行均值检验,应采用( )统计量进行检验。
A.卡方
B.t
C.F
D.Z
正确答案:D
-
第14题:
在假设检验中,下面的说法正确的有( )。
A.建立假设时,有原假设H0和备择假设H1
B.已知μ0,可假设H0:μ=μ0 , H1:μ≠μ0 检验样本均值是否为μ0
C.正态总体σ已知时,μ的显著性水平为a的检验采用 作为检验统计量
作为检验统计量
D.假设H0:μ≤μ0 , H1:μ>μ0 ,是双侧假设检验
E.假设H0:μ=μ0 , H1:μ≠μ0 ,是双侧假设检验答案:A,B,C,E解析:D项,对假设H0:μ≤μ0 , 备择假设H1:μ>μ0 ,是单侧假设检验。 -
第15题:
在对单个正态总体均值的假设检验中,当总体方差已知时,选用()
 答案:B解析:
答案:B解析: -
第16题:
样本平均数抽样分布趋向于正态分布的必要条件是A.总体分布单峰、对称
B.总体均值、方差已知
C.总体分布不限,大样本
D.总体分布正态,样本方差已知答案:C解析:样本平均数的抽样分布形态受三个因素影响:①总体分布是否正态;②总体方差是否已知;③是否大样本。如果总体分布正态、方差是未知的,大样本时,趋向正态分布,而小样本时,趋向于t分布;如果总体分布正态、方差是已知的,无论大小样本,样本平均数的抽样分布都属于正态分布;如果总体分布非正态、方差是未知的,大样本时,趋向于正态分布,而小样本时无解;如果总体分布非正态、方差是已知的,大样本时,趋向于正态分布,而小样本时无解;即无论总体分布是什么形态,无论总体方羞是否已知,只要是大样本,其样本平均数抽样的分布都趋向正态分布。 -
第17题:
μ代表的是()
- A、正态总体均值,表示数据分布的中心位置
- B、数据的平均值
- C、正态总体标准差,表示数据分布的离散程度
- D、数据的极差
正确答案:A -
第18题:
当正态总体的方差已知时,估计总体均值的置信区间使用的分布是()。
- A、正态分布
- B、t分布
- C、卡方分布
- D、F分布
正确答案:A -
第19题:
在假设检验中,显著性水平是()的概率。
- A、原假设为真时被接受
- B、原假设为假时被接受
- C、原假设为真时被拒绝
- D、以上均错误
正确答案:C -
第20题:
在假设检验中,显著性水平α是表示()。
- A、原假设为真时被拒绝的概率
- B、原假设为真时被接受的概率
- C、原假设为假时被接受的概率
- D、原假设为假时被拒绝的概率
- E、是根据样本数据计算出的概率
正确答案:A,E -
第21题:
若一组数据服从正态分布,则下列判断正确的有()。
- A、正态随机变量落入其均值左右各1个标准差内的概率是68.27%
- B、正态随机变量落入其均值左右各2个标准差内的概率是68.27%
- C、正态随机变量落入其均值左右各2个标准差内的概率是95.45%
- D、正态随机变量落入其均值左右各3个标准差内的概率是99.73%
- E、正态随机变量落入其均值左右各4个标准差内的概率是99.73%
正确答案:A,C,D -
第22题:
判断题在假设检验中,方差已知的正态总体均值的检验要计算Z统计量A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
单选题假设正态总体方差未知,欲对其均值进行区间估计或假设检验。从其中抽取较小样本后使用的统计量是()A正态统计量
Bx2统计量
CT统计量
DF统计量
正确答案: B解析: 暂无解析
