现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块板测量其厚度，对其进行方差分析，求得F= 32. 92，查F分布表知在a = 0. 05时临界值为3.89，则结论是（ ）。 A.三台机器生产的薄板厚度在显著性水平0.95上有显著差异 B.三台机器生产的薄板厚度在显著性水平0.95上无显著差异 C.三台机器生产的薄板厚度在显著性水平0.05上有显著差异 D.三台机器生产的薄板厚度在显著性水平0.05上无显著差异

题目
现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块板测量其厚度，对其进行方差分析，求得F= 32. 92，查F分布表知在a = 0. 05时临界值为3.89，则结论是（ ）。
A.三台机器生产的薄板厚度在显著性水平0.95上有显著差异
B.三台机器生产的薄板厚度在显著性水平0.95上无显著差异
C.三台机器生产的薄板厚度在显著性水平0.05上有显著差异
D.三台机器生产的薄板厚度在显著性水平0.05上无显著差异

相似考题

1.方差分析的步骤是以下哪些()A、求平方和并计算自由度B、计算均方和F值C、查F值表进行F检验D、作出判断E、陈列方差分析表

2.在方差分析中所用的检验的拒绝域的临界值来自( )。A．正态分布B．χ2分布C．t分布D．F分布

3.均值为0,方差为1的标准正态分布的平方服从()A、F分布B、正态分布C、卡方分布D、无法确定

4.已知某台机器生产的丝，其直径服从正态分布，钢丝直径的规格界限为TL＝10.95mm，TU＝ 11.05mm。今从一批钢丝中抽取5个样品，测其直径依次为11.02，10.99，10.93，11.01， 10.98，则该批钢丝超出上规格限的概率约为( )。A．Φ(1.825)B．1-Φ(1.03)C．1-Φ(1.825)D．Φ(1.03)

参考答案和解析
答案：C
解析：
由于在a=0.05时临界值为3.89，这表明F0.95(fa，fe)=3.89。而F = 32. 92远大于3. 89，因此三台机器生产的薄板厚度在显著性水平a = 0. 05上有显著差异。
更多“现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块板测量其厚度，对其进行方差分析，求得F= 32. 92，查F分布表知在a = 0. 05时临界值为3.89，则结论是（ ）。 ”相关问题

  • 第1题：

    若取显著性水平α=0.05，查F分布表得临界值是3.48，则( )。

    A．因子A显著

    B．因子A不显著

    C．误差方差σ2的估计为5

    D．误差方差σ2的估计为12.5


    正确答案：AC
    解析：由于，所以因子A显著；误差方差的估计为：MSE=SE/fE=50/10=5。

  • 第2题：

    关于中心极限定理，下列说法正确的是（ ）。
    A.多个随机变量的平均值（仍然是一个随机变量）服从或近似服从正态分布
    B. n个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值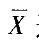
    近似服从正态分布N(μ, σ2/n)
    C.无论什么分布（离散分布或连续分布，正态分布或非正态分布），其样本均值的分布总近似于正态分布
    D.设n个分布一样的随机变量，假如其共同分布为正态分布N(μ, σ2)则样本均值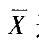仍为正态分布，其均值不变仍为μ，方差为 σ2/n


    答案：B
    解析：
    AC两项成立的前提条件是多个随机变量必须相互独立且同分布；D项要求这些随机变量相互独立。

  • 第3题：

    估计总体方差的置信区间时，其检验统计量服从( )。

    A.正态分布
    B.t分布
    C. 分布
    D.F分布

    答案：C
    解析：

  • 第4题：

    总体服从正态分布，方差未知时，其样本平均数的分布是

    A.X2分布
    B.t分布
    C.F分布
    D.正态分布

    答案：B
    解析：
    总体分布为正态，方差已知，样本平均数的分布为正态分布。总体分布非正态，方差已知，当样本足够大时(n>30)，其样本平均数的分布为渐近正态分布。总体分布为正态，方差未知，样本平均数的分布为t分布。总体分布非正态，方差未知，当样本足够大时(n>30)，其样本乎均数的分布为近似t分布。

  • 第5题：

    方差分析的基本假定是（）。

    • A、总体服从正态分布
    • B、总体服从F分布
    • C、各总体的均值相等
    • D、各总体的方差相同
    • E、观察值独立

    正确答案:A,D,E

  • 第6题：

    若两个总体均服从正态分布，分别从两个总体中随机抽取样本，则两个样本方差之比服从的分布为（）。

    • A、正态分布
    • B、卡方分布
    • C、t分布
    • D、F分布

    正确答案:D

  • 第7题：

    现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块测量其厚度，对其进行方差分析，求得F=32.92，查F分布表知：在α=0.05时的临界值为3.89。下列结论，正确的是：（）

    • A、三台机器生产的薄板平均厚度在显著性水平0.95上有显著差异
    • B、三台机器生产的薄板平均厚度在显著性水平0.95上无显著差异
    • C、三台机器生产的薄板平均厚度在显著性水平0.05上有显著差异
    • D、三台机器生产的薄板平均厚度在显著性水平0.05上无显著差异

    正确答案:C

  • 第8题：

    为了判断不同的生产线所加工的产品厚度是否有显著差异，特选取了企业的四条生产线，从四条生产线的产品中分别随机抽取了10个样本，测量其厚度。通过检验，数据服从正态分布，且满足等方差条件，接下来应该进行的是：（）

    • A、单因子方差分析（one-wayANOVA）
    • B、卡方检验
    • C、双比率检验
    • D、双因子方差分析（two-wayANOVA）

    正确答案:A

  • 第9题：

    多选题
    方差分析的基本假定是（）。
    A

    总体服从正态分布

    B

    总体服从F分布

    C

    各总体的均值相等

    D

    各总体的方差相同

    E

    观察值独立


    正确答案： A,D
    解析： 暂无解析

  • 第10题：

    单选题
    现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块板测量其厚度，对其进行方差分析，求得F=32.92，查F分布表知在α=0.05时临界值为3.89，则结论是（　　）。
    A

    三台机器生产的薄板厚度在显著性水平0.95上有显著差异

    B

    三台机器生产的薄板厚度在显著性水平0.95上无显著差异

    C

    三台机器生产的薄板厚度在显著性水平0.05上有显著差异

    D

    三台机器生产的薄板厚度在显著性水平0.05上无显著差异


    正确答案： D
    解析：
    由于在α=0.05时临界值为3.89，这表明F0.95（fA，fe）=3.89。而F=32.92远大于3.89，因此三台机器生产的薄板厚度在显著性水平α=0.05上有显著差异。

  • 第11题：

    单选题
    某厂生产的产品厚度服从正态分布，厚度的均值为4。某天测得30产品样本的厚度的均值为3.89，欲检验与原来的均值相比是否有所变化，要求的显著性水平为0.05，则其假设形式是（）。
    A

    H0：μ=4；HA：μ≠4

    B

    H0：μ=4；HA：μ>4

    C

    H0：μ=4；HA：μ<4

    D

    H0：μ≠4；HA：μ=4


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    现在三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块板测量其厚度，对其进行方差分析，求得f=32．92，查f分布表知在α=0．05时临界值为3．89，则结论是（）。
    A

    三台机器生产的薄板厚度在显著性水平95上有显著差异

    B

    三台机器生产的薄板厚度在显著性水平95上无显著差异

    C

    三台机器生产的薄板厚度在显著性水平05上有显著差异

    D

    三台机器生产的薄板厚度在显著性水平05上无显著差异


    正确答案： D
    解析： 由于f=32．92>3．89，因此在显著性水平α=0．05时，因子A是显著的。因此选择C。

  • 第13题：

    在方差分析中所用的检验的拒绝域的临界值来自( )。

    A.正态分布
    B.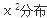
    C.t分布
    D.F分布

    答案：D
    解析：
    方差分析显著性检验用F比值得出。

  • 第14题：

    在方差分析中所用的检验的拒绝域的临界值来自（ ）。A.正态分布 B. x2分布 C. t分布 D. F分布


    答案：D
    解析：
    方差分析显著性检验用F比的值得出。

  • 第15题：

    总体服从正态分布且方差已知时，其样本平均数的分布是

    A.X2分布
    B.t分布
    C.F分布
    D.正态分布

    答案：D
    解析：
    总体分布为正态且方差已知时，其样本平均数的分布为正态分布。

  • 第16题：

    每台机器安装修正板的目的是（）。

    • A、调整内外排温度分布
    • B、调整机器内的真空度分布
    • C、调整内外排膜厚分布
    • D、调整同圈厚度分布

    正确答案:C

  • 第17题：

    从一个正态分布总体中抽取样本，在总体方差已知时样本的平均数和方差分别服从（）分布和（）分布；在总体方差未知时样本的平均数服从（）分布。从两个正态分布总体中抽取样本，在总体方差已知和未知时样本平均数的差分别服从（）分布和（）分布。


    正确答案:正态；卡方；t；正态；t

  • 第18题：

    某厂生产的产品厚度服从正态分布，厚度的均值为4。某天测得30产品样本的厚度的均值为3.89，欲检验与原来的均值相比是否有所变化，要求的显著性水平为0.05，则其假设形式是（）。

    • A、H0：μ=4；HA：μ≠4
    • B、H0：μ=4；HA：μ>4
    • C、H0：μ=4；HA：μ<4
    • D、H0：μ≠4；HA：μ=4

    正确答案:A

  • 第19题：

    某工厂甲乙两条生产线，生产同一种产品，今从每条生产线各取5个产品，测量质量特性如下：甲生产线：8.8，8.4，9.0，8.6，8.5；乙生产线：9.2，8.6，9.0，8.8，8.6；假定它们的方差相等且均服从正态分布，检验平均值有无显著性差异，下述哪些方法可行：（）

    • A、两组数据的t检验
    • B、成对数据的t检验
    • C、单因素方差分析
    • D、F检验

    正确答案:A,C

  • 第20题：

    假设检验中，在小样本的情况下，如果总体不服从正态分布，且总体方差未知，则经过标准化的样本均值服从（）

    • A、Z分布
    • B、t分布
    • C、分布
    • D、F分布

    正确答案:B

  • 第21题：

    单选题
    某机械加工工序生产一种标准的圆环部件，圆环部件的厚度是一个关键尺寸，服从正态分布，产品的均值是32mm，标准差为1mm，生产过程中10个部件为一小批（记为X），作业者对叠放着的每一小批整体测一次厚度，来判断产品是否合格，X的分析近似为（）
    A

    均值为32，方差为1的正态分布

    B

    均值为320，方差为1的正态分布

    C

    均值为320，方差为10的正态分布

    D

    均值为32，方差为10的正态分布


    正确答案： C
    解析： 暂无解析

  • 第22题：

    多选题
    关于成组设计方差分析，正确的说法是（）。
    A

    要求各样本来自同一总体

    B

    要求各总体均服从正态分布

    C

    各样本含量可以不同

    D

    要求各总体方差相等

    E

    查F界值表时的自由度分别为组间自由度和组内自由度


    正确答案： C,E
    解析： 暂无解析

  • 第23题：

    单选题
    现有三台机器生产同规格的铝合金薄板，其厚度分别服从同方差的正态分布，从三台机器上各取五块测量其厚度，对其进行方差分析，求得F=32.92，查F分布表知：在α=0.05时的临界值为3.89。下列结论，正确的是：（）
    A

    三台机器生产的薄板平均厚度在显著性水平0.95上有显著差异

    B

    三台机器生产的薄板平均厚度在显著性水平0.95上无显著差异

    C

    三台机器生产的薄板平均厚度在显著性水平0.05上有显著差异

    D

    三台机器生产的薄板平均厚度在显著性水平0.05上无显著差异


    正确答案： B
    解析： 暂无解析

相关内容