两台机床相互独立工作，需要维修的概率分别是0.3与0.2，下列结果中正确的有 ( )。 A.两台机床都不需要维修的概率是0.56 B.至少有一台机床不需要维修的概率是0. 06 C.至多有一台机床需要维修的概率是0. 94 D.两台机床都需要维修的概率是0. 06 E.只有一台机床需要维修的概率是0.14

题目
两台机床相互独立工作，需要维修的概率分别是0.3与0.2，下列结果中正确的有 ( )。
A.两台机床都不需要维修的概率是0.56
B.至少有一台机床不需要维修的概率是0. 06
C.至多有一台机床需要维修的概率是0. 94
D.两台机床都需要维修的概率是0. 06
E.只有一台机床需要维修的概率是0.14

相似考题

1.电路由元件A与两个并联的元件B、C串联而成,若A,B,C损坏与否是相互独立,且它们损坏的概率依次为 0.3,0.2, 0.1,则电路断路的概率是0.314。()此题为判断题(对，错)。

2.某系统由两个部件组成，其中任何一个部件发生故障都将导致系统故障，故障的发生相互独立，概率分别为0.1与0.3，则系统正常工作的概率为( )。A．0.03B．0.07C．0.27D．0.63

3.某产品可能出现A与B两种缺陷，如果出现缺陷A的概率是0.1，出现缺陷B的概率是0.2，缺陷A的发生与缺陷8的发生相互独立，则该产品无缺陷的概率是（ ）。A.0.70B.0.72C.0.30D.0.80

4.两台机床相互独立工作，需要维修的概率分别是0.3与0.2，两台机床都不需要维修的概率是（ ）。A.0.56B.0.06C.0.94D.0.14

更多“两台机床相互独立工作，需要维修的概率分别是0.3与0.2，下列结果中正确的有 ( )。 ”相关问题

  • 第1题：

    某企业有独立工作的3台服务器，分别运行Web、E-mail、电子商务等业务，由1名网络工程师独立看管，1000小时内它们出故障的概率分别是0.1、0.2及0.15。那么这段时间出现机器故障不能得到及时维修的时间是(68)小时。

    A．30

    B．59

    C．99.41

    D．99.7


    正确答案：B
    解析：分别运行Web、E-mail、电子商务等业务的3台服务器均独立工作，由一名网络工程师看管，1000小时内它们出故障的概率分别是0.1、0.2及0.15。设事件A代表“Web服务器出故障的概率”，事件B代表“E-mail服务器出故障的概率”，事件C代表“电子商务服务器出故障的概率”。那么1000小时内机器出现故障且不能得到及时维修的概率为：
     
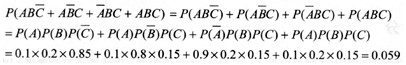
      根据试题上下文信息，试题中“这段时间”意指“1000小时”，因此1000小时内出现机器故障不能得到及时维修的时间是1000×0.059=59小时。

  • 第2题：

    设二维随机变量（X，Y）的概率分布如下表。已知随机事件{X=0}与{X+Y=1}相互独立，则（　　）。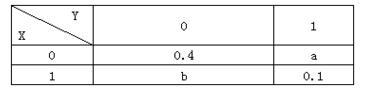

    A．a=0.2，b=0.3
    B．a=0.4，b=0.1
    C．a=0.3，b=0.2
    D．a=0.1，b=0.4

    答案：B
    解析：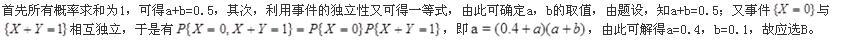

  • 第3题：

    设事件A与B相互独立，则下列结论中，正确的有（ ）。


    答案：A,B,D
    解析：
    。选项A是相互独立的定义，选项B、D是相互独立时的概率乘法公式。选项C、E是互不相容时的效果。

  • 第4题：

    设随机事件A与B相互独立，且P(B)=0.5，P(A-B)=0.3，则P(B-A)=



    A.A0.1
    B.0.2
    C.0.3
    D.0.4

    答案：B
    解析：

  • 第5题：

    某产品可能出现A与B两种缺陷，如果出现缺陷A的概率是0.1，出现缺陷B的概率是0.2，缺陷A的发生与缺陷B的发生相互独立，则该产品无缺陷的概率是 ( )。
    A. 0.70 B. 0.72
    C. 0. 30 D. 0.80


    答案：B
    解析：
    。该产品无缺陷的概率=无缺陷A的概率X无缺陷B的概率=0.9X0. 8=0. 72。

  • 第6题：

    振鸣的概率≤百分之多少？（）

    • A、0.1%
    • B、0.2%
    • C、0.3%
    • D、0.4%

    正确答案:A

  • 第7题：

    电路由元件A与两个并联的元件B、C串联而成，若A，B，C损坏与否是相互独立的，且它们损坏的概率依次为0.3，0.2，0.1，则电路断路的概率是0.314


    正确答案:正确

  • 第8题：

    在键盘输入中，下列是速度与正确率之间关系的有：相互依存，相互矛盾和（）

    • A、相互依赖
    • B、相互独立
    • C、相互制约
    • D、相互对立

    正确答案:D

  • 第9题：

    多选题
    二项分布的随机现象，它满足的条件包括(　　)。
    A

    重复进行n次随机试验，n次试验间相互独立

    B

    每次试验结果不确定，成功的概率为P，失败的概率为2p

    C

    每次试验仅有两个可能结果，且成功的概率为P，失败的概率为1-p

    D

    每次试验前的结果是已知的

    E

    n次试验间不相互独立


    正确答案： A,D
    解析： 由二项分布的定义可知。

  • 第10题：

    多选题
    下列关于二项分布的论述不正确的有（　　）。
    A

    重复进行的n次试验相互不独立

    B

    可用来描述与计点过程相关联的事件

    C

    每次试验仅有两个可能的结果

    D

    每次试验成功的概率均为p，失败的概率为1-p

    E

    每一次试验结果不对其他次试验结果产生影响


    正确答案： C,A
    解析： 由二项分布的基本性质可知:重复进行的n次试验相互独立，故不能用来描述与计点过程相关联的事件。

  • 第11题：

    单选题
    板式轨道混凝土支撑层上裂纹宽度不超过（）mm时，不需要进行任何维修工作。
    A

    0.2

    B

    0.3

    C

    0.4

    D

    0.5


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    一个工人看管三台车床，在一小时内任一台车床不需要人看管的概率为0．8，三台机床工作相互独立，则一小时内三台车床中至少有一台不需要人看管的概率是：（）
    A

    0.875

    B

    0.925

    C

    0.765

    D

    0.992


    正确答案： D
    解析： 暂无解析

  • 第13题：

    一个工人看管3台车床，在1小时内任1台车床不需要人看管的概率为0. 8，3台机床工作相互独立，则1小时内3台车床中至少有1台不需要人看管的概率是：

    A. 0. 875
    B. 0. 925
    C. 0. 765
    D. 0. 992

    答案：D
    解析：
    提示：设A表示“1小时内3台车床至少有1台不要人看管”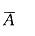，表示“1小时内3台均要人看管”，P(A) = 1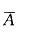-P()，P(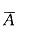)=0.23。或设X为3台车床中不需看管的台数，则X~B (3,0. 8),P(X≥1) =1-P(X=0)。

  • 第14题：

    电路由两个并联电池A与B，再与电池C串联而成，设电池A、B、C损坏的概率分别是0.2，0.2，0.3，求电路发生间断的概率．


    答案：
    解析：

  • 第15题：

    一台设备由三大部件构成,在设备运转过程中各部件需要调整的概率分别为0.1,0.2,0.3,假设各部件的状态相互独立,以X表示同时需要调整的部件数,求E(X),D(X).


    答案：
    解析：

  • 第16题：

    某车间有甲．乙两台机床，已知甲机床停机的概率为0.06，乙机床停机的概率为0.07，甲．乙两车床同时停机的概率是（）

    A.0.13
    B.0.0042
    C.0.03
    D.0.04

    答案：B
    解析：

  • 第17题：

    两台机床相互独立工作，需要维修的概率分别是0.3与0.2，两台机床都不需要维修的概率是（）。
    A. 0. 56 B. 0. 06

    C. 0. 94 D. 0. 14


    答案：A
    解析：
    。设事件A= “甲机床需要维修”，事件B=“乙机床需要维修”，两台机床都不需要维修的概率为 P(AB) = P(A)P(B)=0. 7×0. 8=0. 56。

  • 第18题：

    下列四个向量中，（）是概率向量。

    • A、（0.5，0.3，0.2，0.1）
    • B、（0.2，0.4，0.1，0.2）
    • C、（-0.3，0.6，0.4，0.3）
    • D、（0.6，0.2，0.2，0）

    正确答案:D

  • 第19题：

    板式轨道混凝土支撑层上裂纹宽度不超过（）mm时，不需要进行任何维修工作。

    • A、0.2
    • B、0.3
    • C、0.4
    • D、0.5

    正确答案:D

  • 第20题：

    单选题
    下列四个向量中，（）是概率向量。
    A

    （0.5，0.3，0.2，0.1）

    B

    （0.2，0.4，0.1，0.2）

    C

    （-0.3，0.6，0.4，0.3）

    D

    （0.6，0.2，0.2，0）


    正确答案： A
    解析： 暂无解析

  • 第21题：

    单选题
    某系统由两个部件组成，其中任何一个部件发生故障都将导致系统故障，故障的发生相互独立，概率分别为0.1与0.3，则系统正常工作的概率为（　　）。[2007年真题]
    A

    0.03

    B

    0.07

    C

    0.27

    D

    0.63


    正确答案： C
    解析： 已知两部件故障的发生相互独立，故P（系统正常工作）＝P（第一个部件正常工作）×P（第二个部件正常工作）＝（1-0.1）×（1-0.3）＝0.63。

  • 第22题：

    单选题
    一个工人看管3台车床，在1小时内任1台车床不需要人看管的概率为0.8，3台机床工作相互独立，则1小时内3台车床中至少有1台不需要人看管的概率是：（）
    A

    0.875

    B

    0.925

    C

    0.765

    D

    0.992


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    一台X型号的自动机床在一小时内不需要人照看的概率为0.8000，有四台这种型号的自动机床各自独立工作，则在一小时内至多有2台机床需要工人照看的概率是（）。
    A

    0.1536

    B

    0.1808

    C

    0.5632

    D

    0.9728


    正确答案： B
    解析： 暂无解析

相关内容