一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（ ）

题目
一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（ ）

相似考题

1.一个袋子中有5只黑球3只白球,从袋中任取两只球,若以A表示:“取到的两只球均为白球”;B表示:“取到的两只球同色”。则P(A)=();P(B)=()。

2.一个袋内装有10个球，其中有3个白球，5个红球，2个黑球采取不放回抽样，每次取1件，则第二次取到的是白球的概率是()A、0.6B、0.5C、0.4D、0.3

3.袋子里有20个乒乓球，其中20个黄球，30个白球。现在两个人依次不放回地从袋子中取出一个球，第二个人取出黄球的概率是( )A.1/5B.3/5C.2/5D.4/5

4.一个盒子里有7个无区别的白球，5个无区别的黑球。每次从中随机取走一球，已知前面取走6个，其中3个是白的。试问第6个球是白球的概率()。A、0.6B、0.5C、0.2D、0.75

更多“一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（ ） ”相关问题

  • 第1题：

    有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（ ）。


    答案：D
    解析：
    第一次取到有编号的球的概率为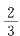，假设取到白色1号球，则第二次必须 取到黑色1号球，其概率为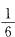。因此前两次恰好摸到同编号的异色球的概率为。。

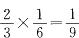  • 第2题：

    盒中有4个白球6个红球，无放回地每次抽取1个，则第二次取到白球的概率是


    A. 2/15
    B. 4/15
    C. 2/5
    D. 3/5

    答案：C
    解析：
    解题指导： 初步学习过概率的考生可能选择用条件概率去做。方法如下：第一次取到白球，第二次取到白球；（4/10）×3/9=12/90。第一次取到黑球，第二次取到白球。（6/10）×4/9=24/90。12/90+24/90=36/90=2/5。故答案为C。

  • 第3题：

    设口袋中有10只红球和15只白球,每次取一个球,取后不放回,则第二次取得红球的概率为_______.


    答案：
    解析：
    设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），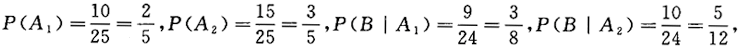　　

    则
    　　

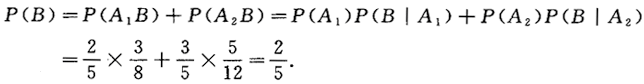
  • 第4题：

    一个布袋中装有大小相同的3个白球、4个红球和2个黑球，每次从袋中摸出一球不再放回。问恰好在第3次取得黑球的概率是多少？


    答案：A
    解析：

  • 第5题：

    有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（ ）。
    A. 4/9 B. 4/15 C. 2/9 D.1/9


    答案：D
    解析：
    D [解析]第一次取到有编号的球的概率为2/3，假设取到白色1号球，则第二次必须取到黑色1号球，其概率为1/6。因此前两次恰好摸到同编号的异色球的概率为2/3 X 1/6 = 1/9。

  • 第6题：

    一个袋子里有8个黑球，8个白球，随机不放回地连续取球五次。每次取出1个球，求最多取到3个白球的概率。


    答案：
    解析：

  • 第7题：

    袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，而且是不放回的摸球：

    （1）求两次摸球均为红球的概率。

    （2）若第一次摸到红球，求第二次摸到黑球的概率。


    答案：
    解析：
    本题主要考查求解随机事件的概率方法。

    （1）利用概率近似等于频率，根据相互独立性，可求解两次摸球都是红球的概率。

    （2）由于第一次摸到红球，从剩余的99个球中摸一个黑球，共有30种可能。

  • 第8题：

    袋中共有5个球，其中3个新球，2个旧球，每次取1个，无放回地取2次，则第二次取到新球的概率是（）．

    • A、3/5
    • B、3/4
    • C、1/2
    • D、3/10

    正确答案:A

  • 第9题：

    设袋中有2个黑球、3个白球，有放回地连续取2次球，每次取一个，则至少取到一个黑球的概率是（）


    正确答案:16/25

  • 第10题：

    单选题
    一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（　　）
    A

    2/15

    B

    4/15

    C

    1/5

    D

    2/5


    正确答案： D
    解析：
    可分成两种情况：①第一次取到白球，第二次也取到白球的概率是：4/10×3/9＝12/90；②第一次取到黑球，第二次取到白球的概率是：6/10×4/9＝24/90，即第二次取到白球的概率为24/90＋12/90＝2/5。

  • 第11题：

    一个袋子里放有10个小球(其中4个白球，6个黑球)，无放回地每次抽取1个，则第二次取到白球的概率是（ ）

    A. 2/15
    B. 4/15
    C. 1/5
    D. 2/5

    答案：D
    解析：
    解题指导： 第一次取到白球，第二次取到白球的机率为4/10*3/9=2/15 ；第一次取到黑球，第二次取到白球的机率为6/10*4/9=4/15 。可知，第二次取到白球的机率为4/15+2/15=2/5,故答案为D。

  • 第12题：

    一个盒子中5个红球,5个白球,现按照如下方式,求取到2个红球和2个白球的概率.
    　　(1)一次性抽取4个球；(2)逐个抽取,取后无放回；(3)逐个抽取,取后放回.


    答案：
    解析：
    【解】(1)设A1={一次性抽取4个球，其中2个红球2个白球），则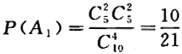
    (2)设A2={逐个抽取4个球，取后不放回，其中2个红球2个白球}，则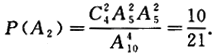

    (3)设A3={逐个抽取4个球，取后放回，其中2个红球2个白球}，则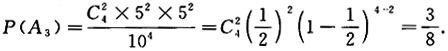

  • 第13题：

    袋中有a个黑球和b个白球,一个一个地取球,求第k次取到黑球的概率（1≤k≤a+b）.


    答案：
    解析：
    方法一基本事件数n=（a+b）!，设Ak={第k次取到黑球），则有利样本点数为a(a+b-1)!，所以

    方法二把所有的球看成不同对象，取k次的基本事件数为，第k次取到黑球所包含的事件数为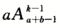，则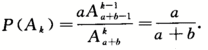

  • 第14题：

    一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球，得到黑球 的概率是2/5，从袋中任意摸两个球,至少有一个是白球的概率是7/9，问袋子里有多少个红球？

    a.l b.2 c.3 d.4


    答案：A
    解析：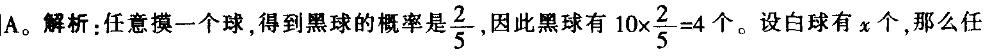

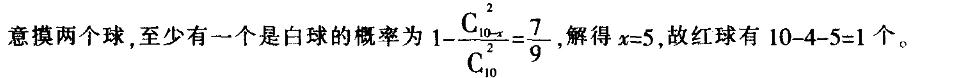
  • 第15题：

    一个袋子里有8个黑球，8个白球，随机不放回连续取球5次，每次取出1个球，求最多取到3个白球的概率. .?


    答案：
    解析：

  • 第16题：

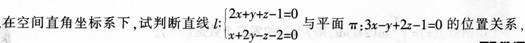
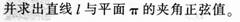    袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中：
    (1)求两次摸球均为红球的概率：
    (2)若第一次摸到红球，求第二次摸到黑球的概率。


    答案：
    解析：
    平面π的法向量为n=(3，-1，2)；

  • 第17题：

    一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中，直至取到红球,然后再取一球，假设每次取球时各个球被取到的可能性相同，求第一、第二次都取到红球的概率（ ）。

    A.7/10
    B.7/15
    C.7/20
    D.7/30

    答案：B
    解析：
    设AB分别表演一、二次取红球，则有P（AB）=P（A）P（B|A）=7/106/9=7/15。

  • 第18题：

    一袋中有2个黑球和若干个白球，现有放回地摸球4次，若至少摸到一个白球的概率是80/81，则袋中白球的个数是（）。


    正确答案:4

  • 第19题：

    袋中有大小相同的黑球7只，白球3只，每次从中任取一只，有放回抽取，记首次抽到黑球时抽取的次数为X，则P{X＝10}＝（）。


    正确答案:0.39*0.7

  • 第20题：

    问答题
    8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求：    (1)第一次取到白球、第二次取到红球的概率；    (2)两次取得一红球一白球的概率．

    正确答案：
    解析： 暂无解析

相关内容