4、将一枚骰子掷2次，若记2次中“点数大于4”出现的次数为Y，则Y服从A．0-1分布B．二项分布C．泊松分布D．几何分布

题目

4、将一枚骰子掷2次，若记2次中“点数大于4”出现的次数为Y，则Y服从

A．0-1分布

B．二项分布

C．泊松分布

D．几何分布

相似考题

1.● 下列事件中，为确定事件是 （9） 。①掷一枚硬币正面朝上。②打开电视机，正在播电视剧③随意翻开一本书，正好翻到第100页④天下雨，地面湿⑤你身高不能长到4米⑥买奖券中特等大奖⑦掷一枚骰子的点数小于8（9）A. ①④⑥B. ②④⑤C. ②③⑥D. ④⑤⑦

2.独立重复地拋一个均匀的骰子n次。设出现点数大于4的次数为un,则对任给的E>0,有:独立重复地拋一个均匀的骰子n次。设出现点数大于4的次数为un,则对任给的E>0,有:请帮忙给出正确答案和分析，谢谢!

3.将一颗骰子掷2次，则2次得到的点数之和为3的概率是 ． （ ）A.AB.BC.CD.D

4.掷一枚骰子,出现的点数不超过 6 是( )A. 不可能事件B. 必然事件C. 随机事件D. 不能判定

更多“4、将一枚骰子掷2次，若记2次中“点数大于4”出现的次数为Y，则Y服从”相关问题

  • 第1题：

    同时掷两颗骰子,则

    出现不同点数的概率为________。

    A．3/4

    B．2/3

    C．5/6

    D．1/4


    正确答案：C

  • 第2题：

    质地均匀的骰子六面分别刻有1-6的点数，掷两次骰子，得到向上一面的两个点数，则下列事件中，发生可能性最大的是()。

    A.点数都是偶数
    B.点数的和为奇数
    C.点数的和小于10
    D.点数的和大于7

    答案：C
    解析：

  • 第3题：

    如下事件发生的概率等于1/4的是()。

    A:抛两枚普通的硬币，出现的均是正面
    B:一个不透明的袋子里装着黑白红蓝四种颜色的球，随机拿出一个恰好为红色球
    C:抛两枚普通的硬币，出现一个正面和一个反面
    D:掷一枚普通的骰子，出现点数小于3
    E:掷两枚普通的骰子，出现点数之和小于

    答案：A,B
    解析：
    A选项，出现两个都是正面的概率=1/2*1/2=1/4；B选项，考查古典概率计算方法的使用，随机拿出一个球可能有4种颜色，红色只占其中一种，所以拿出恰为红色球的概率=1/4；C选项，出现一个正面和一个反面应该包括两种情况：正反、反正，因此其概率=1/4+1/4=1/2；D选项，掷出的点数总共有6种情况，而小于3的只有l和2两种情况，所以其概率=2/6=1/3；E选项，掷两枚骰子，出现的点数和最小为2，即两枚骰子的点数都是1，因此其和小于2是不可能事件，所以概率=0。

  • 第4题：

    独立投骰子两次,X,Y表示投出的点数,令A={X+y=10},B={X>Y},则P(A+B)=_______.


    答案：
    解析：
    P(A)=P{X=4，Y=6}+P{X=5，Y=5）+P{X=6，Y=4）=　　
    P(B)=P{X=2，Y=1}+P{X=3，Y=1}+P{X=3，Y=2}+P{X=4，Y=3}
    　　+P{X=4，Y=2}+P{X=4，Y=1}+P{X=5，Y=4}+P{X=5，Y=3}
    　　+P{X=5,Y=2}+P{X=5,Y=1}+P{X=6,Y=5}+P{X=6,Y=4}
    　　+P{X=6，Y=3}+P{X=6，Y=2）+P{X=6，Y=1）=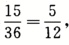
    　P(AB)=P{X=6,Y=4}=，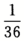
    　　则P(A+B)=P(A)+P(B)-P(AB)=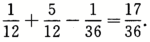

  • 第5题：

    设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.


    答案：1、32
    解析：
    因为X～P(2)，所以E(X)=D(X)=2，于是E(Y)=4E(X)-3=5，D(Y)=16D(X)=32.

  • 第6题：

    如掷一颗骰子，事件A = “出现4点”，事件B = “出现偶数点”，则A、B的关系可以表示为（ ）。



    答案：B
    解析：

  • 第7题：

    掷一颗骰子，A表示“出现奇数点”，B表示“点数不大于3”，A-B则表示（）


    正确答案:出现的点数恰为5

  • 第8题：

    掷一颗骰子，出现的点数为“1点”的概率为六分之一。若将一颗骰子掷6次，则出现“1点”的次数将是（）。

    • A、1次
    • B、大于1次
    • C、小于1次
    • D、上述结果均有可能

    正确答案:D

  • 第9题：

    掷一枚骰子出现的点数小于7，是（）。

    • A、随机现象
    • B、随机事件
    • C、必然事件
    • D、不可能事件

    正确答案:A

  • 第10题：

    单选题
    掷一枚骰子出现的点数小于7，是（）。
    A

    随机现象

    B

    随机事件

    C

    必然事件

    D

    不可能事件


    正确答案： A
    解析： 暂无解析

  • 第11题：

    问答题
    将一枚均匀骰子掷10次，X表示点数6出现的次数，用切比雪夫不等式可估计P{|X-E(X)|

    正确答案：
    解析：

  • 第12题：

    单选题
    将一枚硬币重复掷n次，以X和Y表示正面朝上和反面朝上的次数，则X、Y的相关系数等于（　　）。
    A

    1

    B

    －1

    C

    0

    D

    1/2


    正确答案： D
    解析：
    因为Y＝n－X，故Y与X存在线性关系Y＝aX＋b，且a＝－1＜0，故ρXY＝－1。

  • 第13题：

    将一枚质地均匀的骰子抛掷两次，第一次朝上一面点数设为X，第二次朝上一面点数设为Y，则(X，Y)在双曲线



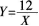
    上的概率为( )。

    A.1/18
    B.1/9
    C.1/6
    D.1/4

    答案：B
    解析：

  • 第14题：

    掷一个普通的骰子，出现点数是3的倍数的概率为()。

    A:1/2
    B:1/3
    C:1/4
    D:1/5

    答案：B
    解析：
    考查古典概率的计算。掷一个普通的骰子可能出现6种情况，点数3的倍数有两个：3和6，所以出现点数是3的倍数的概率为2/6=1/3。

  • 第15题：

    以下两个事件之间呈包含关系的是()。

    A:掷同一枚硬币，“出现正面”与“出现反面”之间
    B:两个互不相识的保险业务员在面对不同客户的签单情况之间
    C:掷一枚普通的骰子，“出现点数为5”与“出现点数为3”之间
    D:参加一次考试，“成绩及格”与“成绩优秀”之间

    答案：D
    解析：
    A选项两个事件是典型的对立事件；B选项由于两个业务员互不相识，面对不同客户，他们之间独立展业，签单情况是相互独立的；C选项两个事件之间是互不相容关系。

  • 第16题：

    设随机变量X服从参数为的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).


    答案：
    解析：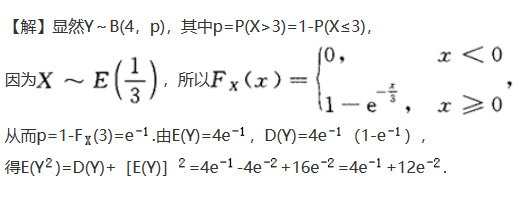

  • 第17题：

    掷一枚正六面体的骰子，掷出的点数不大于3的概率是_________．


    答案：
    解析：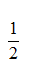

  • 第18题：

    掷一枚均匀的骰子，出现3点的概率为（）；出现3点以下的概率为（）。


    正确答案:1/6；1/3

  • 第19题：

    将一枚硬币重复掷n次，以X和Y分别表示正面向上和反面向上的次数，则X和Y的相关系数等于（）。


    正确答案:－1

  • 第20题：

    掷一颗骰子，出现的点数为“1点”的概率为六分之一。若将一颗骰子掷6次，则出现“1点”的次数将是（）。

    • A、可能1次
    • B、可能2次
    • C、可能大于1次
    • D、上述情况都不会出现

    正确答案:A,B,C,D

  • 第21题：

    设随机变量X服从正态分布N（μ，16），Y服从正态分布N（μ，25）.记p=P（X≤μ-4），g=P（Y≥μ+5），则p与q的大小关系是（）．

    • A、p>q
    • B、p
    • C、p=q
    • D、不能确定

    正确答案:C

  • 第22题：

    多选题
    掷一颗骰子，出现的点数为“1点”的概率为六分之一。若将一颗骰子掷6次，则出现“1点”的次数将是（）。
    A

    可能1次

    B

    可能2次

    C

    可能大于1次

    D

    上述情况都不会出现


    正确答案： C,B
    解析： 暂无解析

  • 第23题：

    单选题
    掷一颗骰子，出现的点数为“1点”的概率为六分之一。若将一颗骰子掷6次，则出现“1点”的次数将是（）。
    A

    1次

    B

    大于1次

    C

    小于1次

    D

    上述结果均有可能


    正确答案： B
    解析： 暂无解析

  • 第24题：

    问答题
    2.将一枚骰子连掷两次，以X表示两次所得的点数之和，以Y表示两次出现的最小点数，分别求X,Y的分布律．

    正确答案：
    解析：

相关内容