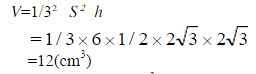(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。 (1)求证:PC∥平面BDE: (2)求三棱锥B-PDE的体积。
题目
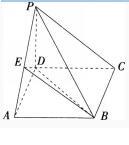
(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。

相似考题
更多“(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。 ”相关问题
-
第1题:
如图,正四面体P-ABC的棱长为a,D、E、F分别为棱PA、PB、PC的中点,G、H、M分别为DE、EF、FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为: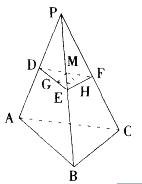 A.1:8
A.1:8
B.1:16
C.1:32
D.1:64答案:D解析:DE=AB/2=a/2,同理三角形GHM的边长为DE/2=a/4。所以三角形GHM和三角形ABC的面积比为边长比的平方1:16。正四面体P-ABC的表面积是三角形ABC面积的4倍,故所求比例为1:16x4=1:64。 -
第2题:
连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体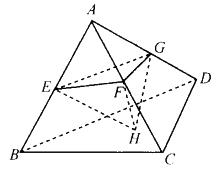
(如右图所示)。问该多面体与正四面体的体积比是多少?( )A. 1 : 8
B. 1 : 6
C. 1:4
D. 1 : 2答案:C解析:如图所示,AEFG与ABCD的边长比为1:2,所以二者的面积比为1 : 4。又因为正四面体A—EFG与正四面体A—BCD高的比为1 : 2,所以,正四面体A—EFG与正四面体A—BCD的体积比为1 : 8,所以该多面体与正四面体A—BCD的体积比为2 : 8,即1 : 4。故本题答案为C。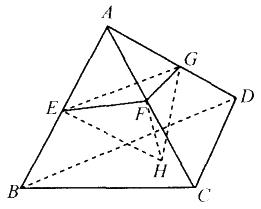
-
第3题:
若正三棱锥底面边长为a,且三条侧棱两两垂直,则它的体积为_____.答案:解析:
-
第4题:
四棱锥P-ABCD(如图7-12所示),用4种不同的颜色涂在四棱锥的各个面上,要求相邻不同色,有( )种涂法.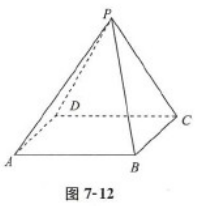 A.40
A.40
B.48
C.60
D.72
E.90答案:D解析: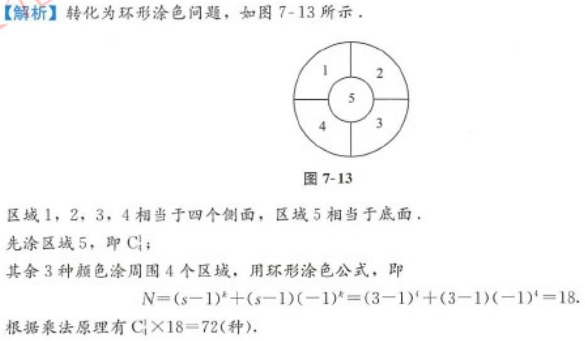
-
第5题:
一只小虫从棱长为2的正三棱锥(如图)中的A点爬到B点(为所在线段的中点),且小虫 只在面OAC和面OCD中移动。问该小虫爬过的最短路程为( )。
 答案:B解析:
答案:B解析: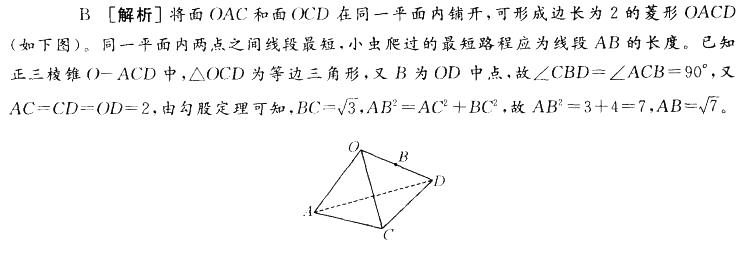
-
第6题:
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P是BC边的中点,AD=2,SA=AB=1。

(1)求证:PD⊥平面SAP;
(2)求三棱锥S-APD的体积。答案:解析:(1)证明:易知在△APD中,,AD=2,满足勾股定理,故PD⊥AP。SA⊥底面ABCD,则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线,PD⊥平面SAP。 (2)
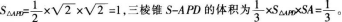
-
第7题:
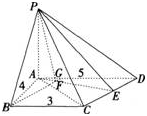
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。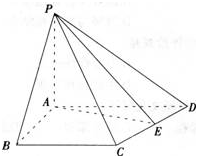 答案:解析:
答案:解析:
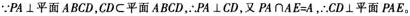

-
第8题:
棱柱体由()构成。
- A、底面
- B、底边
- C、侧棱
- D、侧面
- E、底圆
正确答案:A,B,C,D -
第9题:
棱锥的底面是(),各个棱面都是有一个公共顶点的三角形。
正确答案:多边形 -
第10题:
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为30°。
正确答案:正确 -
第11题:
单选题若正四棱锥的底面为水平面,则其四个棱面在三投影面中的投影不可能()A积聚成直线
B为正垂面
C反映实形
D为缩小的类似形
正确答案: C解析: 暂无解析 -
第12题:
多选题二次对称轴出现的位置一般是()A相对棱的中点
B两底面中心
C一条棱与相对底面的中心
D相对两柱面的中心
正确答案: B,D解析: 暂无解析 -
第13题:
如图,正方体ABCD-A1B1C1D1的棱长为1cm,则三棱锥C-AB1D1的体积是: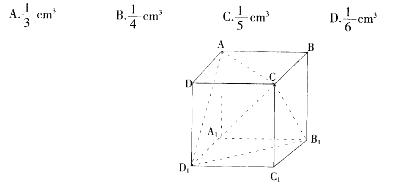 答案:A解析:
答案:A解析:
-
第14题:
正三棱柱ABC—A/B/C/,底面边长为a,侧棱长为h.
(I)求点A到△A/BC所在平面的距离d;
(Ⅱ)在满足d=1的上述正三棱柱中,求侧面积的最小值.答案:解析:
-
第15题:
已知正六棱锥的底面边长为3,侧棱长为5,则该六棱锥的体积为() 答案:A解析:
答案:A解析: -
第16题:
如 ,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
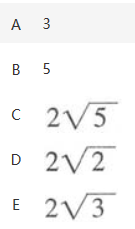 答案:A解析:
答案:A解析:
-
第17题:
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。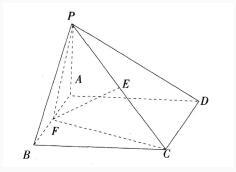 答案:解析:
答案:解析:
-
第18题:
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=

AB=1,M为PB中点。
(1)求证:面PAD⊥面PCD;
(2)求面AMC与面BMC所成二面角的余弦值。答案:解析:(1)∵PA⊥面ABCD,CD⊥AD, ∴由三垂线定理,得CD⊥PD。
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD。
又CD面PCD,∴面PAD⊥面PCD。
(2)作AN⊥CM,垂足为N,连结BN。
在Rt△PAB中,∵M是斜边PB中点,
∴AM=MB.

-
第19题:
已知正六棱锥底面的边长为2cm,侧棱长4cm求正六棱锥的体积?
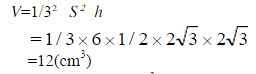
略 -
第20题:
若正四棱柱的底面为水平面,一个棱面为正平面,则其主视图为反映前后棱面实形的矩形线框。
正确答案:正确 -
第21题:
二次对称轴出现的位置一般是()
- A、相对棱的中点
- B、两底面中心
- C、一条棱与相对底面的中心
- D、相对两柱面的中心
正确答案:A,B,C,D -
第22题:
判断题若正四棱柱的底面为水平面,一个棱面为正平面,则其主视图为反映前后棱面实形的矩形线框。A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
判断题正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为30°。A对
B错
正确答案: 对解析: 暂无解析