在Rt△ABC中,A.C=90°,sin A=1/2,则∠a=________.
题目
相似考题
更多“在Rt△ABC中,A.C=90°,sin A=1/2,则∠a=________.”相关问题
-
第1题:
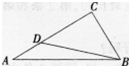
如图Rt△ABC中,∠ACB=90。,D是AC上靠近A的三等分点,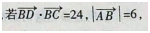
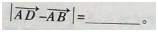
 答案:解析:
答案:解析:
解析:

-
第2题:
在△ABC中,三个内角A,B,C所对的边分别为a,b,c,已知(1/2)sin2A=sinB?sinC。
(1)若a=2b,求tanC的值;(4分)
(2)若A=π/3,b=1,且b答案:解析:
-
第3题:
在 RC 串联电路中,已知外加电压:u(t) = 20 + 90sin(ωt) + 30sin(3ωt + 50°) + 10sin(5ωt + 10°)V,电路中电流:i(t) = 1.5 + 1. 3sin(ωt + 85. 3°) + 6sin(3ωt + 45°) + 2. 5sin(5ωt - 60. 8°) A,则电路的平均功率P为( )。
A. 124. 12W B. 128. 12W C. 145. 28W D. 134. 28W答案:B解析:解相同频率(同次谐波)的电压和电流相乘才能产生功率,因此电路的平均功率为:
P=P0+P1+P3+P5
=20X1. 5+ 1/2 X 90 X 1. 3 X cos85. 3°+1/2 X 30 X 6 X cos5° + 1/2 X 10 X 2. 5 X cos70. 8°
=128. 12W
答案:B -
第4题:
如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为__________。
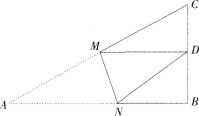 答案:解析:
答案:解析:
-
第5题:
以下是某学生证明勾股定理“在Rt△ABC中,∠C=90°,求证a2+b2=c2”的过程:因为a=csinA,b=ccosA,所以a2+b2=c2sin2A+c2cos2A=c2(sin2A+cos2A)=c2。
以上证明所犯的错误主要是( )。
A.偷换论题
B.虚假论据
C.循环论证
D.不能推出答案:C解析:该学生在论证中用到sin2A+cos2A=1,而这个公式成立依赖于a2+b2=c2,因此该学生的论证犯了循环论证的错误。 -
第6题:
某工频正弦电流,当t=0,i(0)=5A为最大值,则该电流解析式是()。
- A、i=5√2sin(100πt-90°)
- B、i=5√2sin(100πt+90°)
- C、i=5sin(100πt+90°)
- D、i=5sin(100πt-90°)
正确答案:C -
第7题:
sin45ocos45o+sin30o+sin75otg120ocos90o的结果为:()。
- A、1/2
- B、(21/2)/2
- C、1
- D、(31/2)/2
正确答案:C -
第8题:
已知i1=30Sin(100πt十I5°),i2=40Sin(100πt十105°),则i1+i2的初相位是()。
- A、90°
- B、9°
- C、68.l°
- D、31.9°
正确答案:C -
第9题:
已知两个正弦量为u1=20√2sin(314t-60°)V,u2=20√2sin(314t+30°)V,则()。
- A、u1比u2滞后30°
- B、u1比u2超前30°
- C、u1比u2滞后90°
- D、u1比u2超前90°
正确答案:C -
第10题:
已知两正弦量,u1=20sin(ωt+π/6),u2=40sin(ωt-π/3),则u1比u2()。
- A、超前30°
- B、滞后30°
- C、滞后90°
- D、超前90°
正确答案:D -
第11题:
判断题已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1和S2,则S1+S2的值等于4π。A对
B错
正确答案: 对解析: 暂无解析 -
第12题:
单选题设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=( )。A1/sin2(sin1)
Bsin2(sin1)
C-sin2(sin1)
D-1/sin2(sin1)
正确答案: B解析:
φ′(4)=1/f′(0)=1/sin2(sin1)。 -
第13题:
如图,Rt△ABC中,∠ABC=90o,AB=28 cm,以AB为直径的半圆与AC相交,图中的阴影部分①的面积比⑦的面积少28.28 cm2,求BC的长(π取3.14)。
 答案:解析:
答案:解析:
-
第14题:
已知两个共用一个顶点的等腰Rt△ABC,等腰Rt△CEF,∠ABC=∠CEF= 90o,连接AF,M是AF的中点,连接MB,ME。
(1)如图1,当CB与CE在同一直线上时,若CB=a,CE=2a,求BM,ME的长;
(2)如图2,当∠BCE=45o时,求证:BM=ME。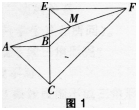
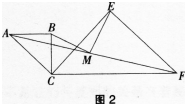 答案:解析:(1)如图,延长AB交CF于点D,则易知△BCD为等腰直角三角形,
答案:解析:(1)如图,延长AB交CF于点D,则易知△BCD为等腰直角三角形,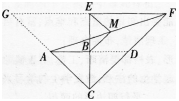

(2)如图,延长AB交CE于点D,连接DF,则△BCD为等腰直角三角形,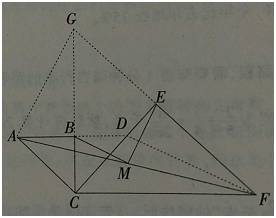
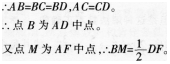
延长FE与CB交于点G,连接AG,则易知△CEG为等腰直角三角形,
∴CE=EF=EG,CF=CG。
∴点E为FG中点。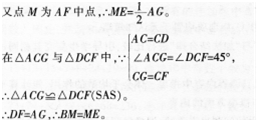
-
第15题:
如图5,在△ABC中,∠ABC=90o,∠CBD=40o,AC∥BD,则∠A=__________度。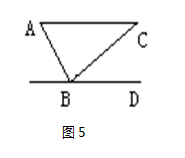 答案:解析:50
答案:解析:50 -
第16题:
在Rt△ABC中,∠C=90°,若cosA=3/5,则tanB的值是( )。A.3/5
B.3/4
C.4/5
D.4/3答案:B解析:{图] -
第17题:
已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。
正确答案:正确 -
第18题:
已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1和S2,则S1+S2的值等于4π。
正确答案:错误 -
第19题:
已知一个正弦量为u1=10sin(314t+90°)A,u2=10sin(314t+30°),则()。
- A、u1比u2超前60°
- B、u2比u1滞后60°
- C、u1比u2超前90°
- D、不能判断相位差
正确答案:A,B -
第20题:
已知2个正弦交流电压V1=310sin(314t-30°)V,V2=310sin(314t+90°)V,则V1和V2的相位差为 -120°而()超前()。
正确答案: V2;V1 -
第21题:
己知两正弦量,u1=20sin(ωt+π/6),u2=40sin(ωt-π/3),则u1比u2()。
- A、超前30°
- B、滞后30°
- C、滞后90°
- D、超前90°
正确答案:D -
第22题:
已知il=30sin(100t+15°),i2=40sin(100t+105°),则i1+i2的初相位是()。
- A、90°
- B、-90°
- C、68.1°
- D、31.9°
正确答案:C -
第23题:
单选题设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=( )。Asin2(sin1)
B1/sin2(sin1)
Csin(sin1)
D1/sin(sin1)
正确答案: D解析:
φ′(4)=1/f′(0)=1/sin2(sin1)。
