一个正方体的高增加10cm,得到新长方体的表面积比原正方体表面积增加120cm,原正方体体积是( ).A.9cm3 B.12cm3 C.18cm3 D.27cm3
题目
一个正方体的高增加10cm,得到新长方体的表面积比原正方体表面积增加120cm,原正方体体积是( ).
A.9cm3
B.12cm3
C.18cm3
D.27cm3
B.12cm3
C.18cm3
D.27cm3
相似考题
参考答案和解析
答案:D
解析:
如下图所示,高增加10cm后,增加的表面积为四个侧面积.设原正方体的棱长为acm,则有4×10a=120,解得a=3,则原正方体的体积为33=27cm3.


更多“一个正方体的高增加10cm,得到新长方体的表面积比原正方体表面积增加120cm,原正方体体积是( ).”相关问题
-
第1题:
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
正确答案:D
要使这些小正方体的表面积总和最小,那么小正方体的边长要尽可能大。64、40、24的最大公约数为B,因此小正方体的边长为8cm,共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。 -
第2题:
一个正方体和一个长方体拼成一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。原来正方体的表面积是多少平方厘米?
正确答案:750000平方厘米
-
第3题:
用n个棱长是a cm的小正方体可以摆出“一”字形长方体,如图,n个小正方体拼在一起 时,这个长方体表面积是_______cm2。
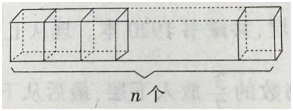 答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。
答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。 -
第4题:
小学数学《长方体和正方体的表面积》
一、考题回顾
题目来源:5月18日 上午 天津市 面试考题
试讲题目
1.题目:长方体和正方体的表面积
2.内容:


3.基本要求:
(1)10分钟试讲;
(2)引导学生理解长方体和正方体的表面积计算公式;
(3)要有适当板书。
答辩题目
1.本节课的教学目标是什么?
2.如何做好课堂提问?答案:解析:二、考题解析
【教学过程】
(一)导入新课
课件出示:丰富的生活场景;一些长方体、正方体纸盒;漂亮的礼品盒。
提出问题:
(1)前面我们看到的主要是什么形状的物体?
(2)单独出示一个漂亮的礼品盒(出示图:长6厘米、宽5厘米、高4厘米)。想做一个这样的纸盒,至少需要多少硬纸板?
引出课题。
(二)新知探索
1.表面积的概念
提问:如果把手中的长方体纸盒、正方体纸盒展开会是什么样子呢?
学生操作,得出如下图:
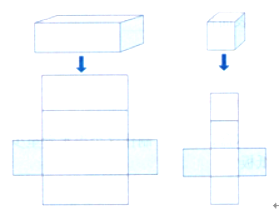
引导学生小组合作,在展开图中标出原来长方体、正方体的上、下、前、后、左、右6个面,并观察。
提问:哪些面的面积相等?每个面的长和宽与长方体的长宽高有什么关系?
预设:长方体的上下面积、前后面积、左右的面相等。正方体的六个面都相等。
教师给出表面积的概念:长方体或正方体6个面的总面积,叫做它的表面积。
2.表面积公式
例1:做一个微波炉的包装箱,至少需要多少平方米的硬纸板?

引导学生表示出上下、前后、左右面的面积,得出长方体表面积的计算方法。
例2:一个正方体墨水盒,棱长为6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?

引导学生通过合作,自己去探求正方体表面积的计算方法,通过对微波炉的包装,引导学生掌握正确计算长方体面积的计算方法。
总结:长方体表面积=(长×宽+长×高+宽×高)×2;正方体表面积=边长×边长×6
(三)课堂练习
做一做题目:
要做这样一个衣柜的布罩,至少需要用布多少平方米?
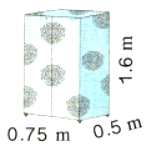
(四)小结作业
这节课我们一起学习了什么?你有哪些收获?
利用本节课所学的知识解决生活中遇到的问题。
【板书设计】
长方体和正方体的表面积
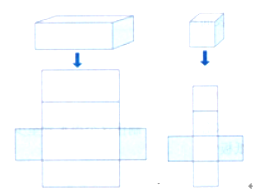
长方体或正方体6个面的总面积,叫做它的表面积。
例1:
例2:
长方体表面积=(长×宽+长×高+宽×高)×2;正方体表面积=边长×边长×6
【答辩题目解析】
1.本节课的教学目标是什么?
【参考答案】
知识与技能:能够知道什么是长方体和正方体表面积,学会长方体和正方体表面积计算方法,并能够运用方法解决实际问题。
过程与方法:通过动手实践、自主探索和合作交流的学习方式参与活动之中探索本质,锻炼分析、归纳、概括、推理能力。
情感态度与价值观:经历过程体验成功,激发学习兴趣,树立自信,形成良好的学习习惯。
2.如何做好课堂提问?
【参考答案】
课堂提问是启发学生非常重要的手段。要想做好,需要从以下几个方面入手:
首先,深钻教材是有效提问的前提。教师只有钻研教材,把握知识的来龙去脉,教学目标才能明确,教学重难点才能清晰,提问才能更具有针对性。
其次,教师需要了解学生情况。了解学生的生活经验,了解学生的知识背景,了解学生已有的知识与技能水平,这样才能依据学生情况提出更有针对性的问题,实现有效提问。
然后,教师还要合理设计提问的问题。把握好问题的形式。
最后,提问应该给予学生足够的思考与反应时间,才能达到最好的效果。 -
第5题:
以下哪个选项适合作为五年级下册《长方体和正方体的表面积》教学的知识目标()。
- A、让学生理解长方体和正方体的表面积意义,初步学会长方体和正方体面积的计算方法
- B、通过小组合作、观察思考等解决问题的方法
- C、让学生感受到数学与生活的密切联系
- D、培养学生探求意识和探求能力
正确答案:A -
第6题:
单选题在棱长为1的正方体上切下两个角,所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体,六面体体积为原正方体体积的1/24,则六面体表面积为原正方体表面积的:A1/4
B1/6
C1/8
D1/10
正确答案: A解析: -
第7题:
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
正确答案:D
要使这些小正方体的表面积总和最小,那么小正方体的边长要尽可能大。64、40、24的最大公约数为8,因此小正方体的边长为8cm,共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。 -
第8题:
在棱长为1的正方体上切下两个角,所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体,六面体体积为原正方体体积的1/24,则六面体表面积为原正方体表面积的:A.1/4
B.1/6
C.1/8
D.1/10答案:C解析:由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥,设切下角的直角边为x,则六面体体积=2×三棱锥体积=2×(1/3)×(x2/2)×x=1/24,解得x=1/2。所以六面体每个面是直角边为1/2的等腰直角三角形,六面体的每个面相当于边长为1的正方形面积的1,所以六面体的表面积为原正方体的1/8。故本题选C。 -
第9题:
一个长方体木块恰能切割成五个正方体木块,五个正方体木块表面积之和比原来的长方体木块的表面积增加了200cm2。则长方体木块的体积为多少?A.625cm3
B.125cm3
C.500cm3
D.750cm3答案:A解析:第一步,本题考查几何问题,属于立体几何类。
第二步,如图所示,长方体分为5个小正方体,增加了4×2=8(个)阴影部分小正方形的面积,则每个小正方形面积为200÷8=25(cm2),边长为5cm。那么大长方体的体积为5×25×5=625(cm3)。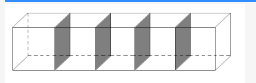
因此,选择A选项。 -
第10题:
体积相等的球和正方体,它们的表面积的大小关系是()。
- A、S球>S正方体
- B、S球=S正方体
- C、S球<S正方体
- D、不能确定
正确答案:C -
第11题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100㎝2
B400㎝2
C500㎝2
D600㎝2
正确答案: B解析:
在一个边长为20㎝的大正方体中挖去1个边长为10㎝的小正方体,则大正方体原有的6个面只有其中1个面的面积减少了100㎝2,而小正方体则多出了5个100㎝2的面,因此大正方体的面积增加了400㎝2。 -
第12题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100cm2
B400cm2
C500cm2
D600cm2
正确答案: C解析:
在一个边长为20cm的大正方体中挖去一个边长为10cm的小正方体,则大正方体原有的6个面只有其中一个面的面积减少了100cm2,而小正方体则多出了5个100cm2的面,因此大正方体的面积增加了400cm2。
