下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)． (1)求出图象与戈轴的交点A，B的坐标；存在，请说明理由； ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围．

题目

下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)．
(1)求出图象与戈轴的交点A，B的坐标；

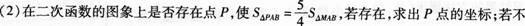
存在，请说明理由；
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围．

相似考题

1.作出函数y=3-2x的图象，根据图象回答下列问题：（1）y的值随着x值增大而__________;（2）图象与x轴的交点坐标是_________________，与y轴的交点坐标是_______________；（3）当x__________时，y＞0 。

2.在同一直角坐标系内作出下列函数的图像：（1）y=4x-1；（2）y=4x+1；（3）y=-4x-1；

3.根据二次函数图象上三个点的坐标，求出函数解析式：（1）（-1，3）（1，3）（2，6）；（2）（-1，-1）（0，-2）（1，1）；（3）（-1，0）（3，0）（1，-5）；（4）（1，2）（3，0）（-2，20）。

4.在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。（1）这几个图象之间有什么差别，又有什么联系？（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？

更多“下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)． ”相关问题

第1题：

已知函数 y=x²-4x+3。
（1）画出函数的图象；
（2）观察图象，当x取哪些值时，函数值为0？
第2题：

11 、点 A （ 2 ， y 1 ）、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关
系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ）．

正确答案：
<

考点：二次函数图象上点的坐标特征。

分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．

解答：解：∵二次函数y=x²﹣2x+1的图象的对称轴是x=1，

在对称轴的右面y随x的增大而增大，

∵点A（2，y1）、B（3，y2）是二次函数y=x²﹣2x+1的图象上两点，

23，

∴y1y2．

故答案为：．

点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．
第3题：

已知一次函数的图象经过点A（2，1），B（－1，－3）
（1）求此一次函数的解析式；
（2）求此一次函数的图象与x轴、y轴的交点坐标；
（3）求此一次函数的图象与两坐标轴所围成的三角形面积。

正确答案：
（1）y=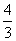x －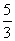
    (2)与x轴的交点坐标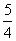（,0）；与y轴的交点坐标(0,－ )
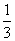    (3)面积为
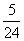
第4题：

当a≠0时，函数y=ax+1与y=a/x在同一坐标中图象可能是（）。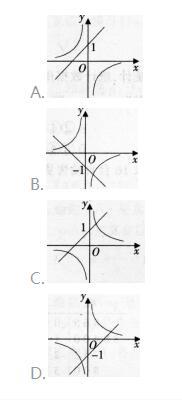

答案：C
解析：
第5题：

二次函数y＝2x2＋mx－5在区间(－∞，－1)内是减函数，在区间(－1，＋∞)内是增函数，则m的值是（　　）

A.4
B.－4
C.2
D.－2

答案：A
解析：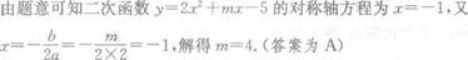
第6题：

下图所示电路中，Y恒为1的图是（）。

答案：C
解析：
第7题：

函数y=2x-2的图象与坐标轴的交点共有__________个．

答案：
解析：
2
第8题：

关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。

A.图象开口向上
B.图象的对称轴为直线x=1
C.图象有最低点
D.图象的顶点坐标(-1，2)

答案：D
解析：
由二次函数图象的性质可知，其开口方向向下，有最大值2，对称轴为x=-1，顶点坐标(-1，2)。二次函数y=a(x+h)2+k(α≠0)中，α决定了二次函数图象的开口方向，顶点坐标为(-h，k)。
第9题：

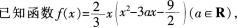
若函数f(x)的图象上点P(1，m)处的切线方程为3x-y+b=0，则m的值为__________。

答案：
解析：
第10题：

设变量x=-6，y=-4，m=10，n=8，则下列表达式中值为false的是（）。
- A、x+m<=y+n
- B、x>0ANDy<0
- C、m=nORx
- D、x+yn）
正确答案:B
第11题：

填空题
二次函数的图像与x轴交点横坐标为－2和1，且通过点（2，4），则其函数解析式为____．

正确答案： y=x²+x-2
解析：
设函数解析式为y＝ax²＋bx＋c，将三个点（－2，0）（1，0）（2，4）代入求解，得到a＝1，b＝1，c＝－2；所以函数解析式为y＝x²＋x－2．
第12题：

填空题
多媒体计算机处理图象和视频，首先必须将连续的图象函数f（x，y）进行空间和幅值的离散化处理，空间连续坐标（x，y）的离散化，叫做（）；f（x，y）颜色的离散化，称之为（）。两种离散化结合在一起，叫做（）。

正确答案：采样,量化,数字化
解析：暂无解析
第13题：

画出函数 y=x²-2x-3的图象，利用图象回答：
（1）方程 x²-2x-3=0 的解是什么；
（2）x取什么值时，函数值大于0 ；
（3）x取什么值时，函数值小于0 。
第14题：

已知m是整数，且一次函数y=(m+4)x+m+2的图象不过第二象限，则m= ；

正确答案：
－3或－2
第15题：

A.常数k＜-1
B.函数f(x)在定义域范围内，y随着x的增大而减小
C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜n
D.函数f(x)图象对称轴的直线方程是y=x

答案：C
解析：
由图象可知常数k＞0，A项错误；当x＞0时，y随着x的增大而减小，当x＜0时，y随着x的增大而减小，B选项说法不严谨，错误；由反比例函数的公式可得，m=-k＜0，

m＜n，C正确；函数f(x)图象对称轴有两条，y=x和y=-x，D错误。
第16题：

定义[a，b，c]为函数y=ax2+bc+c的特征数，下面给出特征数为[ 2m ，1-m，-1-m]的函数的一些结论：
①当m=-3时，函数图象的顶点坐标是{1/3,-(8/3)}；
②当m>0时，函数图象截石轴所得的线段长度大于3/2；
③当m<0时，函数在x>1/4时，y随x的增大而减小；
④当m≠0时，函数图象经过同一个点。
其中正确的结论有()。

A.②③④
B.①②④
C.③④
D.②④

答案：D
解析：
特征数[2m，1-m，-l-m]的函数为y=2mx2+(1-m)x+(-1-m)。①当m=-3时，y=-6x2+4x+
第17题：

顶点在坐标原点，准线方程为y=4的抛物线方程式（　　）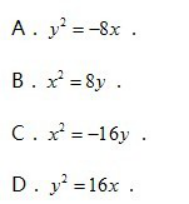

答案：C
解析：
第18题：

下列函数图象与y=f（x）的图象关于原点对称的是（　　）

A.y=-f（x）
B.y=f（-x）
C.y=-f（-x）
D.y=｜f（x）｜

答案：C
解析：
第19题：

初中数学《二次函数的图象与性质》
一、考题回顾
题目来源:5月18日上午湖北省黄石市面试考题
试讲题目
1.题目：二次函数的图象与性质
2.内容：

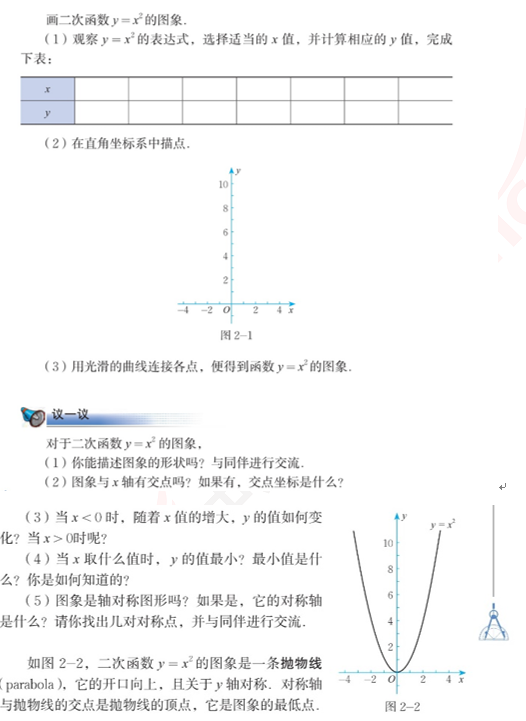
3.基本要求：
(1)掌握五点作图法的画图方法，能根据图象理解二次函数的性质;
(2)试讲十分钟;
(3)要有合适的板书。
答辩题目
1.二次函数的顶点坐标如何表示?
2.确定二次函数的表达式需要几个条件?

答案：
解析：
二、考题解析
【教学过程】
(一)导入新课
回顾一次函数和反比例函数，提问：一次函数和反比例函数的图象是什么形状?
预设：一次函数的图象是一条直线，反比例函数的图象是双曲线。
追问：二次函数的图象是什么形状的?有什么性质?

教师资格考试考前黑钻押题，瑞牛题库软件考前更新，下载链接 www.niutk.com
第20题：

由函数y=ex的图象与y=-2x，x=1，x=3所围成的封闭面积为_______。

答案：
解析：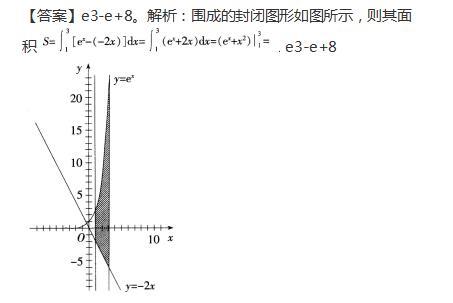
第21题：

已知函数 (x)=sin(ωx+φ)(ω>0)的图象如下图所示，则ω=（　　）。

答案：B
解析：
第22题：

多媒体计算机处理图象和视频，首先必须将连续的图象函数f（x，y）进行空间和幅值的离散化处理，空间连续坐标（x，y）的离散化，叫做（）；f（x，y）颜色的离散化，称之为（）。两种离散化结合在一起，叫做（）。

正确答案:采样；量化；数字化
第23题：

填空题
二次函数y＝－x2＋2x＋n的图象与x轴的一个交点为（3，0），则n＝____．

正确答案： 3
解析：
将（3，0）代人y＝－x²＋2x＋n，得－3²＋2×3＋n＝0，解得n＝3．

题目

相似考题

更多“下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)． ”相关问题

相关内容