小赵和小李是两位竞走运动员，小赵从甲地出发，小李同时从乙地出发，相向而行，在两地之间往返练习。第一次相遇地点距甲地1.4千米，第二次相遇地点距乙地0.6千米。当他们两人第四次相遇时，地点距甲地有多远？A2.6千米 B.2.4千米 C.1.8千米 D.1.5千米
题目
小赵和小李是两位竞走运动员，小赵从甲地出发，小李同时从乙地出发，相向而行，在两地之间往返练习。第一次相遇地点距甲地1.4千米，第二次相遇地点距乙地0.6千米。当他们两人第四次相遇时，地点距甲地有多远？
A2.6千米 B.2.4千米 C.1.8千米 D.1.5千米
相似考题
更多“小赵和小李是两位竞走运动员，小赵从甲地出发，小李同时从乙地出发，相向而行，在两地之间往返练习。第一次相遇地点距甲地1.4千米，第二次相遇地点距乙地0.6千米。当他们两人第四次相遇时，地点距甲地有多远？A2.6千米 B.2.4千米 C.1.8千米 D.1.5千米”相关问题
-
第1题：
甲、乙二人往返于A、B两地，甲从A地、乙从8地同时出发，相向而行，两人第一次在距A地2千米处相遇，第二次在距A地6千米处相遇，则A、B两地的距离为（ ）。 A．6千米 B．7千米 C．8千米 D．9千米
正确答案：A
设A、B两地的距离为S，则第一次两人相遇时乙走了(S－2)千米，甲走了2千米，第二次两人相遇时若为迎面相遇，则甲走了(2S－6)千米，乙走了(S＋6)千米，由于两人速度不变，故可得
，解得S＝6，或S＝0(舍)，即A、B两地相距6千米，也就是说第二次相遇在B地，故不需再考虑追及相遇的情况。故选A。
-
第2题：
小赵和小李是两位竞走运动员，小赵从甲地出发，小李同时从乙地出发，相向而行，在两地之间往返练习。第一次相遇地点距甲地1.4千米，第二次相遇地点距乙地0.6千米。当他们两人第四次相遇时，地点距甲地有多远？
A2.6千米
B.2.4千米
C.1.8千米
D.1.5千米
正确答案：A
-
第3题：
甲乙两地铁路线长1880千米，从甲地到乙地开出一辆动车，每小时行驶160千米，3小时后，从乙地到甲地开出一辆高铁，经4小时后与动车相遇，则高铁每小时行驶A. 180千米
B. 210千米
C. 200千米
D. 190千米答案：D解析：由题可知，3小时候动车所行距离为160×3=480千米。总距离为1880千米，则动车和高铁相遇过程中所走的总距离=1880-480=1400千米。由相遇问题公式：相遇距离=速度和×相遇时间，设高铁的速度为x，则1400=（160+x）×4，解出高铁的速度x=190千米/小时。选择D。 -
第4题：
一辆汽车将一批货物从甲地送往乙地再返回，甲乙两地相距100千米，
汽车每小时行驶90千米。汽车开到中途丙地发现有东西落在甲地，立即返回去取，
然后再送去乙地，最后花了3小时才返回甲地。问丙地距乙地多少千米?A: 30千米
B: 35千米
C: 65千米
D: 70千米答案：C解析：3小时走的总路程为甲乙路程的2倍+甲丙路程的2倍，则甲丙相距(90x3—100x2)÷
2=35千米。则丙地距乙地100-35=65千米，故选C。 -
第5题：
甲乙两车同时从A 、B 两地相向而行，在距B 地54千米处相遇，它们各自到达对方车站后立即返回，在距A 地42千米处相遇。请问A 、B 两地相距多少千米：
A 120
B 100
C 90
D 80答案：A解析：
-
第6题：
午9时一辆货车从甲地出发前往乙她，同时一辆客车从乙地出发前往甲地，中午12时两车相遇。已知货车和客车的时速分别是90千米和100千米，则当客车到达甲地时，货车距乙地的距离为（ ）A.30千米
B.43千米
C.45千米
D.50千米
E.57千米答案：E解析： -
第7题：
甲、乙两地之间有一条公路，李明从甲地出发步行往乙地；同时张平从乙地出发骑摩托车往甲地。80 分钟后两人在途中相遇。张平到达甲地后马上折回往乙地，在第一次相遇后又经过20分钟张平在途中追上李明。张平到达乙地后又马上折回甲地，这样一直下去，当李明到达乙地时，张平追上李明的次数是多少？（ ）
A. 3 B. 4 C. 5 D. 6答案：B解析：画线段图如下:
设从第一次相遇后到张平第一次追上李明时李明走了x千米，则相同时间内张平走了xX(80/20)X2+x=9x(千米)，即在相同时间内，张平速度是李明速度的9x/x==9(倍)。这就是说，李明从甲地步行到乙地时，张平骑摩托车行走了9个全程。很明显，其中有5个全程是从乙地到甲地，有4个全程是从甲地到乙地。从甲地到乙地张平每走一个全程，必然追上李明一次。因此，张平共追上李明4次。故本题正确答案为B。 -
第8题：
小赵和小李驾车同时分别从甲、乙两地出发，匀速相向而行，两车相遇后小赵继续行驶30千米到达乙地，随后立刻折返，在距离甲地40千米的地方追上小李的车。问甲、乙两地间的距离在以下哪个范围内？A.超过120千米
B.110—120千米之间
C.100—110千米之间
D.不到100千米答案：C解析：本题属于行程问题。
根据题意，得到运动轨迹如图所示：
假设甲乙两地之间的距离为S，则在第一次相遇时，S小赵=S－30，S小李=30。在折返后小赵追上小李时，他们二人的总路程分别为S小赵=2S－40，S小李=S－40。小赵、小李所用的时间相同，且速度一直保持不变，速度之比=路程之比，即
，整理得S2-130S+2400=0，解得
，
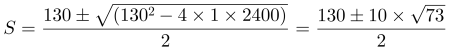介于8和9之间，分别将8、9代入原式得S1=（130+80）/2=105，S2=（130+90）/2=110，所以甲乙两地的距离范围为105—110之间，根据选项，只有C项符合。
因此，选择C选项。 -
第9题：
甲、乙两车分别从A、B两地同时出发相向而行，6小时后相遇在C点，如果甲车速度不变，乙车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇地点距C点12千米；如果乙车速度不变，甲车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇地点距C点16千米，甲车原来每小时行多少千米？（）
- A、20
- B、40
- C、10
- D、30
正确答案:D -
第10题：
单选题甲、乙两地相距100千米，一辆汽车和一台拖拉机都从甲地开往乙地，汽车出发时，拖拉机已开了15千米。当汽车到达乙地时，拖拉机距乙地还有10千米。那么汽车是在距乙地多少千米时追上拖拉机的？（ ）A60千米
B50千米
C40千米
D30千米
正确答案： C解析：
汽车和拖拉机的速度比为100:（100－15－10）＝4:3，设相遇地点距乙地S千米，则4/3＝（100－S）/（100－S－15），得S＝40。 -
第11题：
单选题甲、乙两地铁路线长1880千米，从甲地到乙地开出一辆动车，每小时行驶160千米，3小时后，从乙地到甲地开出一辆高铁，经4小时后与动车相遇，则高铁每小时行驶（）。A180千米
B190千米
C200千米
D210千米
正确答案： B解析： 暂无解析 -
第12题：
甲、乙两地之间有一条公路。李明从甲地出发步行去乙地，同时张平从乙地出发骑摩托车去甲地，80分钟后两人在途中相遇。张平到达甲地后马上折回乙地，在第一次相遇后又经过20分钟在途中追上李明。张平达到乙地后又马上折回甲地，这样一直下去。当李明到达乙在，张平共追上李明多少次?（ ） A．4 B．5 C．6 D．7
A.一步一步的斗。
-
第13题：
：甲、乙两车同时从A、B两地相向而行，在距B地54千米处相遇，它们各自到达对方车站后立即返回，在距A地42千米处相遇。问A、B两地相距多少千米?(提示：相遇时它们行了3个全程)（ ）。
A．120
B．150
C．180
D．200
正确答案：A本题考查的是相遇问题。设A、B两地相距s千米，令甲的速度是x千米/小时，乙的速度为y千米/4,时。
两车同时从A、B两地相向而行，在距B地54千米处相遇时，
根据他们相遇的时间相等得：(s一54)/x=54/y………………①
再次相遇时，甲乙所用时间同样是相等的，则：
(s-54+42)/y=(54+S一42)/x………………………………②
由①、②整理可得S2—120s一0
解之得Sl一o(不合题意舍去)娩一l20
故A、B两地相距l20千米。答案选A。 -
第14题：
甲、乙两地之间有一条公路，李明从甲地出发步行往乙地；同时张平从乙地出发骑摩托车往甲地。80分钟后两人在途中相遇。张平到达甲地后马上折回往乙地，在第一次相遇后又经过20分钟张平在途中追上李明。张平到达乙地后又马上折回往甲地，这样一直下去，当李明到达乙地时，张平追上李明的次数是多少？（ ）A. 3
B. 4
C. 5
D. 6答案：B解析：画线段图如下：
设从第一次相遇后到张平第一次追上李明时李明走了x千米，则相同时间内张平走了xX (80/20) X2+x=9x(千米)，即在相同时间内，张平速度是李明速度的：9x/x=9(倍)。这就是说，李明从甲地步行到乙地时，张平骑摩托车行走了9个全程。很明显，其中有5个全程是从乙地到甲地，有4个全程是从甲地到乙地。从甲地到乙地张平每走一个全程，必然追上李明一次。因此，张平共追上李明4次。故本题正确答 案为B。 -
第15题：
甲乙两人从P，Q两地同时出发相向匀速而行，5小时后于M点相遇。若其他条件不变，甲每小时多行4千米，乙速度不变，则相遇地点距M点6千米；若甲速度不变，乙每小时多行4千米，则相遇地点距M点12千米，则甲乙两人最初的速度之比为：
A 2:1
B 2:3
C 5:8
D 4:3答案：A解析：
-
第16题：
小张从甲地出发匀速前往乙地，同时小李和小王从乙地出发匀速前往甲地，小张和小李在途中的丙地相遇，小张和小王在途中的丁相遇，已知小张的速度比小李快一半，小王的速度比小李慢一半，则丙丁两地之间的距离与甲乙之间的距离之比为：A.2:15
B.1:4
C.3:20
D.1:15答案：C解析：
-
第17题：
小车和客车从甲地开往乙地，货车从乙地开往甲地，他们同时出发，货车与小车相遇20分钟后又遇客车。已知小车、货车和客车的是速度分别为75千米/小时、60千米/小时和50千米/小时，则甲、乙两地的距离是（ ）A．205千米
B．203千米
C．201千米
D．198千米答案：D解析：行程问题。设货车与小车从出发到相遇的时间为t，总路程为S。根据迎面相遇模型公式，列式可得：(75+60)×t=S
(50+60)×(t+1/3)=S，解得S=198。D项当选。 -
第18题：
小张和小马分别从甲、乙两地同时出发，相向而行，出发时他们的速度之比是5∶3，第一次相遇后，小张的速度提高了20％，小马的速度提高了50％，这样，当小张到达乙地时，小马离甲地还有11千米，那么甲、乙两地的距离是多少？A.20千米
B.24千米
C.32千米
D.40千米答案：C解析：设甲、乙两地相距8ｘ千米，由于小张和小马的速度之比为5∶3，所以当他们初次相遇时小张走了5ｘ千米，小马走了3ｘ千米。之后二人速度改变，他们的速度之比变为［5×（1＋20％）］∶［3×（1＋50％）］＝4∶3，此后小张继续走3ｘ千米到达乙地，则相同时间内小马走的距离是(3/4)×3x=(9/4)x千米，此时小马距离甲地还有11千米，即5x-(9/4)x=11，解得ｘ＝4，则甲、乙两地相距4×8＝32千米。故本题选C。 -
第19题：
甲乙两车同时从A、B两地出发相向而行，在距B地54千米处相遇，它们各自到达对方车站后立即返回，在距A地42千米处相遇。请问A、B两地相距多少千米？（）
- A、120
- B、100
- C、90
- D、80
正确答案:A -
第20题：
单选题甲乙两车从A、B两地相向而行，在距B地54千米相遇，他们各自到达对方车站后立即返回，在距A地42千米处相遇，请问A、B两地相距多少千米？A120
B100
C90
D80
正确答案： D解析： -
第21题：
单选题甲乙两车分别从ab两地出发相向而行,两车在距B 地64千米处第一次相遇,相遇后两车仍以原来的速度继续前行,并在到达对方起点后立即返回,两车在距A地48千米处第二次相遇,请问两车相遇地点相距多少千米?A24
B28
C32
D36
正确答案： A解析：