公务员考试数学题问当甲乙丙各有多少人做事,才能生产出甲乙丙刚好配套的零件?县农机厂金车间共有77个工人,已知每天每人可以加工5个甲零件或者4个乙零件或者3个丙零件。但是3个甲,1个乙和9个丙才能刚刚凑成一套零件。问当甲乙丙各有多少人做事,才能生产出甲乙丙刚好配套的零件?
题目
公务员考试数学题问当甲乙丙各有多少人做事,才能生产出甲乙丙刚好配套的零件?
县农机厂金车间共有77个工人,已知每天每人可以加工5个甲零件或者4个乙零件或者3个丙零件。但是3个甲,1个乙和9个丙才能刚刚凑成一套零件。问当甲乙丙各有多少人做事,才能生产出甲乙丙刚好配套的零件?
相似考题
参考答案和解析
答案D 代放法,3乘人数是9的倍数就AD,再用其中一个代一好了,代的结果D 60*3/9=20套
20/4=5
20*3/5=12
或者 设做甲的60个人 总共300件 乙100件 丙900件 则乙需要25个 丙需要100个 60:25:300=12:5:60 所以60人做丙
或者设甲X乙Y丙Z 5X/3=4Y/1=3Z/9=K
X+Y+Z=77
解出Z=60
更多“公务员考试数学题问当甲乙丙各有多少人做事,才能生产出甲乙丙刚好配套的零件? ”相关问题
-
第1题:
甲公司和乙公司原各有债务5万元,后来甲、乙公司合并为丙公司,其中甲乙丙公司均为法人,那么对10万元债务的处理方式为( )
A.由甲乙公司各自偿还5万元
B.由甲偿还10万元债务
C.由丙偿还
D.债务自然消灭
参考答案:C
-
第2题:
单独完成某项工程,甲队需要36天,乙队需要30天,丙队需要32天,如果安排合作施工,按照甲乙、乙丙、丙甲、甲乙……的顺序按天轮转,问完成这项工作时,甲工作了多少天?A.11天整
B.11天多
C.12天整
D.12天多答案:A解析:第一步,本题考查工程问题,属于时间类,用赋值法解题。
第二步,给定甲乙丙三队单独完成时间,时间类工程问题,赋值工程总量为时间36、30、32的最小公倍数1440,则甲、乙、丙的效率分别为40、48、45。将甲乙、乙丙、丙甲每3天作为一个周期,每个周期中每队工作两天,则每个周期的效率之和为(40+48+45)×2=266。则1440÷266=5…110,即工作5个周期还剩余110的工作量。
第三步,5个周期甲工作了10天,每个工作周期的第一天甲乙工作量和为40+48=88,第二天乙丙工作量和是48+45=93,剩余110的工作量在第二天可完成,甲只需再工作1天,因此甲一共工作了11天整。
因此,选择A选项。 -
第3题:
2、甲乙分别在山上伐木,为图方便各自将砍伐的原木从山上滚下,不料其中一根木头砸伤了山下的行人丙,且无法确定是谁推下的木头。丙的损害应该由:()
A.甲乙承担按份责任
B.甲乙承担连带责任
C.甲乙丙分担
D.丙自己承担
【解析】B 共同危险行为,又称准共同侵权行为,指二人以上实施危及他人人身或者财产安全的行为并造成损害后果,不能确定实际侵害行为人的情况。题干中无意思联络,且不能确定侵权人,所以属于共同危险,共同危险行为,有所有行为人承担连带责任。 -
第4题:
甲乙丙三人在2008年的年龄(周岁)之和为60,2010年甲是丙年龄的两倍,2011年乙是丙年龄的两倍,问甲是哪一年出生的?( )A. 1988
B. 1986
C. 1984
D. 1982答案:C解析:设甲、乙、丙在2008年的岁数为X、Y、Z。由题意有
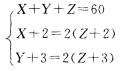
解得X = 24,则甲是在1984年出生的。 -
第5题:
甲乙丙三人共同取得一笔收入30万,根据各自的贡献大小进行分配,若仅在甲乙之间分配,则甲将分得3/5的份额;若仅在乙、丙之间分配,则丙将分得1/3的份额。问,若在甲乙丙三人之间分配,则甲能获得( )万元的收入。A.10 B.15 C.18 D.20答案:B解析:根据题意可知,其贡献大小为甲∶乙=3∶2,乙∶丙=2∶1,故三者贡献比为甲∶乙∶丙=3∶2∶1,按此比例分配,甲可获得30×[3/(3+2+1)]=15万。
