反对称矩阵的主对角线上的元素和为0。()
题目
反对称矩阵的主对角线上的元素和为0。()
相似考题
参考答案和解析
更多“反对称矩阵的主对角线上的元素和为0。()”相关问题
-
第1题：
已知对称矩阵An*n(Ai,j=Aj,i)的主对角线元素全部为O，若用一维数组B仅存储矩阵A的下三角区域的所有元素(不包括主对角线元素)，则数组B的大小为( )。
A．n(n-1)
B．n2／2
C．n(n-1)／2
D．n(n+1)／2
正确答案：C
解析：以4阶对称矩阵为例说明。如果一个4阶对称矩阵及其下三角区域分别如下图所示，那么它的下三角区域(不包括对角线)的元素个数为1+2+3。
依此类推，对于n阶对称矩阵，其下三角区域的元素个数为l+2+3+…n-1。 -
第2题：
下列程序的功能是( )。 main() { static int s[3][3]={1，2，3，4，5，6，7，8，9，)，m，n； for(m=0；m＜3；m++) { for(n=0；n＜=m；n++) printf("%d"，s[m][n])；printf("\n')； } }
A．输出3×3矩阵的下三角的元素
B．输出3×3矩阵的上三角的元素
C．输出3×3矩阵的对角线上的元素
D．输出3×3矩阵的元素
正确答案：A
解析：本题使用了一个双重for循环，外循环变量m的变化范围是0～2，而内循环变量n的变化范围从0～m，所以执行循环体时(m，n)的值依次为(0，0)，(1，0)，(1，1)，(2，0)，(2，1)，(2，2)，故输出的是3×3矩阵的下三角元素。所以应该选择A。 -
第3题：
设3阶实对称矩阵A的各行元素之和都为3,向量
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵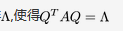
答案：解析：
-
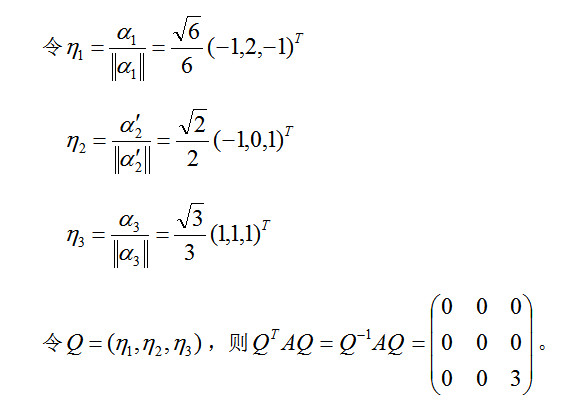
第4题：
与n阶单位矩阵E相似的矩阵是
A.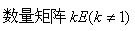
B.对角矩阵D（主对角元素不为1）
C.单位矩阵E
D.任意n阶矩阵A答案：C解析： -
第5题：
设有 n 阶三对角矩阵A,即非零元素都位于主对角线以及与主对角线平行且紧邻的两条对 角线上,现对该矩阵进行按行压缩存储,若其压储空间用数组 B 表示,A 的元素下标从 0 开 始,B 的元素下标从 1 开始。已知 A[0,0]存储在 B[1],A[n-1,n-1]存储在 B[3n-2],那么非零元素 A[i,j]（0≤iA.2i+j-1
B.2i+j
C.2i+j+1
D.3i-j+1答案：C解析：三对角矩阵如下
将i=0，j=0与1=n-1，j=n-1分别带入选项中，可得选项C。第6题：
证明：只要适当地排列顶点的次序，就能使有向无环图的邻接矩阵中主对角线以下的元素全部为0。
正确答案:任意n个结点的有向无环图都可以得到一个拓扑序列。设拓扑序列为v0v1v2…vn-1，我们来证明此时的邻接矩阵A为上三角矩阵。证明采用反证法。
假设此时的邻接矩阵不是上三角矩阵，那么，存在下标i和j（i>j），使得A[i][j]不等于零，即图中存在从vi到vj的一条有向边。由拓扑序列的定义可知，在任意拓扑序列中，vi的位置一定在vj之前，而在上述拓扑序列v0v1v2…vn-1中，由于i>j，即vi的位置在vj之后，导致矛盾。因此命题正确。第7题：
若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。
正确答案:上；三角矩阵第8题：
马尔可夫预测法中的转移概率矩阵对角线上元素之和为1。
正确答案:错误第9题：
单选题在一个概率矩阵中，（）的概率值之和需等于1。A每一个行向量
B每一个列向量
C两条对角线上元素
D主对角线上元素
正确答案： D解析： 暂无解析第10题：
填空题下面的语句显示输出8行8列数组h的主对角线上的所有元素，请补充完整：for（i=0；i<8；i++）cout<<（）<<’’；正确答案： h[i][i]解析： 暂无解析第11题：
问答题证明：只要适当地排列顶点的次序，就能使有向无环图的邻接矩阵中主对角线以下的元素全部为0。正确答案： 任意n个结点的有向无环图都可以得到一个拓扑序列。设拓扑序列为v0v1v2…vn-1，我们来证明此时的邻接矩阵A为上三角矩阵。证明采用反证法。
假设此时的邻接矩阵不是上三角矩阵，那么，存在下标i和j（i>j），使得A[i][j]不等于零，即图中存在从vi到vj的一条有向边。由拓扑序列的定义可知，在任意拓扑序列中，vi的位置一定在vj之前，而在上述拓扑序列v0v1v2…vn-1中，由于i>j，即vi的位置在vj之后，导致矛盾。因此命题正确。解析： 暂无解析第12题：
填空题若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。正确答案： 上,三角矩阵解析： 暂无解析第13题：
将一个n阶三对角矩阵A的三条对角线上的元素按行压缩存放于一个一维数组B中， A[0][0]存放于B[0]中。对于任意给定数组元素A[i][j]，它应是数组A中第______行的元素。
正确答案：2i+j-3
2i+j-3 解析：在三对角矩阵中，按行压缩存储，其转换公式为k=2i+j-3。第14题：
设有 n 阶三对角矩阵 A，即非零元素都位于主对角线以及与主对角线平行且紧邻的两条对角线上，现对该矩阵进行按行压缩存储，若其压储空间用数组 B 表示，A 的元素下标从 0开始，B 的元素下标从 1 开始。已知 A［0,0］存储在 B［1］，A［n－1，n－1］存储在 B［3n-2］，那么非零元素 A［i,j］（0≤ i＜n，0≤ j＜n，│i-j│≤1）存储在 B（ ）A.2i+j-1
B.2i+j
C.2i+j+1
D.3i-j+1答案：C解析：第15题：
电力系统节点导纳矩阵中，某行（或某列）非对角元素之和的绝对值一定小于主对角元素的绝对值。（ ）答案：对解析：第16题：
下面的说法中，不正确的是()。A.对角矩阵只需存放非零元素即可
B.稀疏矩阵中值为零的元素较多，因此可以采用三元组表方法存储
C.稀疏矩阵中大量值为零的元素分布有规律，因此可以采用三元组表方法存储
D.对称矩阵只需存放包括主对角线元素在内的下(或上)三角的元素即可答案：C解析：稀疏矩阵中大量值为零的元素分布没有规律，因此采用三元组表存储。如果零元素的分布有规律，就没有必要存储非零元素的行号和列号，而需要按其压缩规律找出相应的映象函数。第17题：
在一个概率矩阵中，（）的概率值之和需等于1。
- A、每一个行向量
- B、每一个列向量
- C、两条对角线上元素
- D、主对角线上元素
正确答案:A第18题：
若矩阵中所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值全为0，则称为（）。
正确答案:三对角矩阵第19题：
下面的语句显示输出8行8列数组h的主对角线上的所有元素，请补充完整：for（i=0；i<8；i++）cout<<（）<<’’；
正确答案:h[i][i]第20题：
用对称分量法计算不对称故障，当三相阻抗完全对称时，则其序阻抗矩阵Zsc的非对角元素为（）。
正确答案:零第21题：
填空题若矩阵中所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值全为0，则称为（）。正确答案： 三对角矩阵解析： 暂无解析第22题：
单选题求解线性方程组的高斯主元消去法的条件为（ ）。A三对角矩阵
B上三角矩阵
C对称正定矩阵
D各类大型稀疏矩阵
正确答案： B解析： 暂无解析第23题：
单选题设有一个M*N的矩阵已经存放在一个M行N列的数组x中，且有以下程序段：sum=0;for(i=0;iA矩阵两条对角线元素之和
B矩阵所有不靠边元素之和
C矩阵所有元素之和
D矩阵所有靠边元素之和
正确答案： A解析：
程序执行过程为：第一个for循环实现对第一列和第N列求和。第二个for循环在上一个for循环结果上实现对第一行和第M行从第二个元素到第N-1个元素的求和，总体来说，就是矩阵所有靠边元素之和，答案选择D选项。