通过Z-W变换，将Z特征方程变成W特征方程，这样就可以利用Routh稳定性准则来判断W特征方程的根是否在W平面的左半面，也就是Z特征方程是否有根位于Z平面的单位圆内。

题目

通过Z-W变换，将Z特征方程变成W特征方程，这样就可以利用Routh稳定性准则来判断W特征方程的根是否在W平面的左半面，也就是Z特征方程是否有根位于Z平面的单位圆内。

相似考题

1.一个系统稳定的必要和充分条件有()。A、特征方程的所有根必须为负实数B、特征方程的所有根必须为具有负实部的复数C、特征方程的所有根必须为正实数D、特征方程的所有根必须为具有正实部的复数

2.利用乃奎斯特稳定性判据判断系统的稳定性时，z=p-N中的z表示()。A.闭环特征方程在s右半平面根的个数B.闭环特征方程在s左半平面根的个数C.特征函数在右半平面的零点数D.特征函数在左半平面的零点数

3.用Z变换解常线性差分方程和用拉氏变换求解微分方程是类似的。()

4.判别系统稳定性的出发点是系统特征方程的根必须为负实根或负实部的复数根,即系统的特征根必须全部在复平面的右半平面是系统稳定的充要条件。()此题为判断题(对，错)。

更多“通过Z-W变换，将Z特征方程变成W特征方程，这样就可以利用Routh稳定性准则来判断W特征方程的根是否在W平面的左半面，也就是Z特征方程是否有根位于Z平面的单位圆内。”相关问题

  • 第1题：

    离散系统在时域内常用()来描述。

    A.欧拉方程

    B.微分方程

    C.差分方程

    D.Z传递函数


    正确答案：C

  • 第2题：

    一阶过程控制系统稳定的条件是（）

    • A、特征根为正，微分方程系数都大于零
    • B、特征根为负，微分方程系数都大于零
    • C、特征根为正，微分方程系数都小于零
    • D、特征根为负，微分方程系数都小于零

    正确答案:B

  • 第3题：

    根轨迹法是由尹文斯（W·R·Evans）于1948年提出的一种求解闭环特征方程根的简便图解方法。


    正确答案:正确

  • 第4题：

    离散控制系统不稳定的充要条件是特征方程的部分根位于Z平面（）

    • A、单位圆外
    • B、单位圆内
    • C、单位圆上
    • D、Z平面上z=-1线左侧

    正确答案:A

  • 第5题：

    水流的两个截面面积为w，下列方程中不属于恒定流连续方程的是（）

    • A、Q1=Q2；
    • B、w1v1=w2v2；
    • C、v1/v2=w2/w1；
    • D、Z1+P1/γ+α1v12/2g=Z2+P2/γ+α2v22/2g+hw1-2。

    正确答案:D

  • 第6题：

    用微机实现数字控制算法的基本思想是把D（z）变换为（）

    • A、连续方程
    • B、离散方程
    • C、差分方程
    • D、微分方程

    正确答案:C

  • 第7题：

    由特征方程的劳斯表所得的辅助方程F（s）＝0的根一定也是原特征方程的根。


    正确答案:正确

  • 第8题：

    频率特性不必解出特征方程的根。


    正确答案:正确

  • 第9题：

    当且仅当特征方程的全部特征根分布在z平面上（），即 特征根的模均小于1，相应的线性离散系统是（）。


    正确答案:单位圆内；稳定的

  • 第10题：

    问答题
    怎样根据特征方程的特征根以判定车辆蛇行运动稳定性？

    正确答案： 根据求出的特征根实部的正负判断车辆蛇行运动的稳定性，当所有的特征根实部均为负时，车辆系统蛇行运动稳定，存在特征根为零或者负时，车辆系统的蛇行运动不稳定。
    解析： 暂无解析

  • 第11题：

    多选题
    一个系统稳定的充分和必要条件是系统（）
    A

    特征方程的根全都为负实数

    B

    全部极点都位于[S]平面的左半部（不含虚轴）

    C

    全部极点都位于[S]平面的右半部

    D

    特征方程系数全部为正

    E

    劳斯表中第一列各元素均大于零


    正确答案： E,B
    解析： 暂无解析

  • 第12题：

    单选题
    利用奶奎斯特稳定性判据判断系统的稳定性时，Z=P-N中的Z表示意义为（）。
    A

    开环传递函数零点在S左半平面的个数

    B

    开环传递函数零点在S右半平面的个数

    C

    闭环传递函数零点在S右半平面的个数

    D

    闭环特征方程的根在S右半平面的个数


    正确答案： A
    解析： 暂无解析

  • 第13题：

    在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。
    (1)求。的值及直线Z的直角坐标方程；
    (2)圆C的参数方程为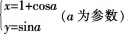试判断直线Z与圆C的位置关系。


    答案：
    解析：
    所以直线l与圆C相交。

  • 第14题：

    Routh判据指出，Routh表中第一列各元符号改变的次数等于系统特征方程具有（）特征根的个数。


    正确答案:正实部

  • 第15题：

    S平面上根轨迹与虚轴的交点可以通过特征方程的劳斯表辅助方程求得。


    正确答案:正确

  • 第16题：

    利用奶奎斯特稳定性判据判断系统的稳定性时，Z=P-N中的Z表示意义为（）。

    • A、开环传递函数零点在S左半平面的个数
    • B、开环传递函数零点在S右半平面的个数
    • C、闭环传递函数零点在S右半平面的个数
    • D、闭环特征方程的根在S右半平面的个数

    正确答案:D

  • 第17题：

    爱因斯坦曾提出一个成功方程式：X+Y+Z=W，其中W代表成功，X代表艰苦劳动，Z代表少说空话，Y代表（）

    • A、正确的方法
    • B、永不服输
    • C、团结协作
    • D、爱岗敬业

    正确答案:A

  • 第18题：

    一个系统稳定的充分和必要条件是系统（）

    • A、特征方程的根全都为负实数
    • B、全部极点都位于[S]平面的左半部（不含虚轴）
    • C、全部极点都位于[S]平面的右半部
    • D、特征方程系数全部为正
    • E、劳斯表中第一列各元素均大于零

    正确答案:A,B

  • 第19题：

    ω变换可以将z平面的特征方程转换为ω平面的特征方程，从而应用（）判定线性离散控制系统的稳定性。


    正确答案:劳斯判据

  • 第20题：

    离散系统的特征方程D（z）=z3-3z2+2.25z-0.5=0是稳定的。


    正确答案:错误

  • 第21题：

    离散系统在时域内常用（）来描述。

    • A、欧拉方程
    • B、微分方程
    • C、差分方程
    • D、Z传递函数

    正确答案:C

  • 第22题：

    单选题
    一阶过程控制系统稳定的条件是（）
    A

    特征根为正，微分方程系数都大于零

    B

    特征根为负，微分方程系数都大于零

    C

    特征根为正，微分方程系数都小于零

    D

    特征根为负，微分方程系数都小于零


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    利用变量替换u＝x，v＝y/x一定可以把方程x∂z/∂x＋y∂z/∂y＝z化为新方程（　　）。
    A

    u∂z/∂u＝z

    B

    ∂z/∂v＝z

    C

    u∂z/∂v＝z

    D

    v∂z/∂u＝z


    正确答案： B
    解析：
    由x∂z/∂x＋y∂z/∂y＝z，得∂z/∂x＝（∂z/∂u）·1＋（∂z/∂v）（－y/x2），∂z/∂y＝（1/x）（∂z/∂v）。
    故x∂z/∂x＋y∂z/∂y＝x∂z/∂u－（y/x）（∂z/∂v）＋（y/x）（∂z/∂v）＝x∂z/∂u＝z。
    而u＝x，故u∂z/∂u＝z。

  • 第24题：

    填空题
    Routh判据指出，Routh表中第一列各元符号改变的次数等于系统特征方程具有（）特征根的个数。

    正确答案： 正实部
    解析： 暂无解析

相关内容