图示a)、b)系统中的均质圆盘质量、半径均相同，角速度与角加速度分别为ω1、 ω2 和 α1、α2，则有:A. α1 =α2 B. α1 >α2 C. α1 2 D. ω1 =ω2
题目
图示a)、b)系统中的均质圆盘质量、半径均相同，角速度与角加速度分别为ω1、 ω2 和 α1、α2，则有:
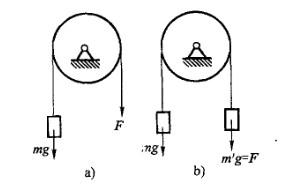
A. α1 =α2 B. α1 >α2 C. α1 2 D. ω1 =ω2
A. α1 =α2 B. α1 >α2 C. α1 2 D. ω1 =ω2
相似考题
更多“图示a)、b)系统中的均质圆盘质量、半径均相同，角速度与角加速度分别为ω1、 ω2 和 α1、α2，则有: ”相关问题
-
第1题：
偏心轮为均质圆盘，其质量为m，半径为R，偏心距OC=R/2。若在图示位置时，轮绕O轴转动的角速度为ω，角加速度为α，则该轮的惯性力系向O点简化的主矢FI和主矩MIO的大小为：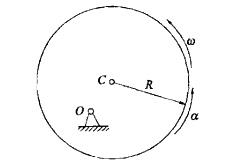
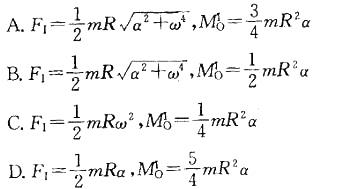答案：A解析：提示：MIO=-JOα，其中 JO = JC + m* OC2 。 -
第2题：
图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆盘中心O的水平轴转动，角速度为ω，角加速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（ ）。
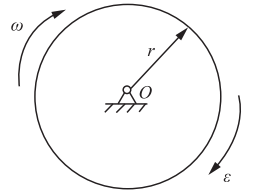
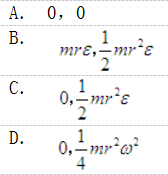答案：C解析：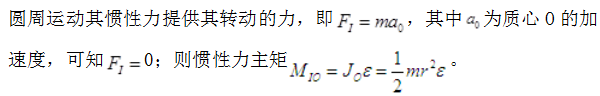
-
第3题：
均质圆盘质量为m，半径为R，在铅垂面绕内O轴转动，图示瞬间角速度为ω，则其对O轴的动量矩大小为（ ）。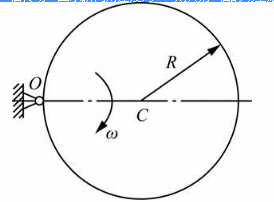
A．mRω
B．mRω/2
C．mR2ω/2
D．3mR2ω/2答案：D解析：根据质点的动量矩公式，体系对O点的动量矩为：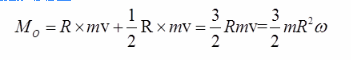
-
第4题：
杆OA绕固定轴O转动，圆盘绕动轴A转动，已知杆长l=20cm，圆盘r=10cm，在图示位置时，杆的角速度及角加速度分别为w=4rad/s，ε=3rad/s2；圆盘相对于OA的角速度和角加速度分别为wr=6rad/s，εr=4rad/s2。则圆盘上M1点绝对加速度为( )。
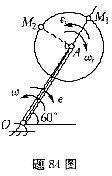
A．a1=363cm/s2
B．a1=463cm/s2
C．a1=563cm/s2
D．a1=663cm/s2答案：A解析：牵连运动为转动，此时加速度合成时，将多一个科氏加速度 -
第5题：
均质圆盘质量为m，半径为R，再铅垂面内绕o轴转动，图示瞬吋角速度为w，则其对o轴的动量矩和动能的大小为：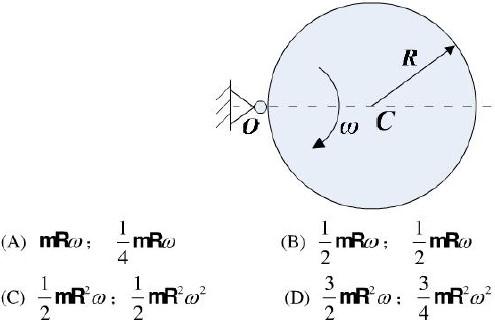
答案：C解析：解：选C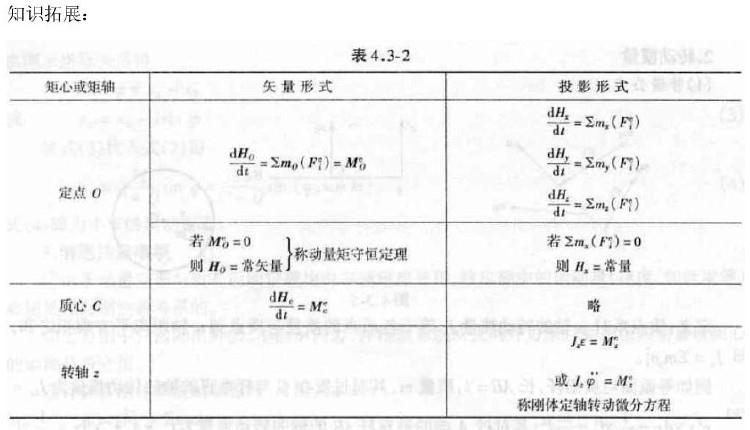
-
第6题：
质量为m，半径为R的均质圆盘，绕垂直于图面的水平轴O转动，其角速度为ω，在图示瞬时，角加速度为零，盘心C在其最低位置，此时将圆盘的惯性力系向O点简化， 其惯性力主矢和惯性力主矩的大小分别为：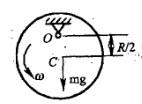
答案：A解析：提示：根据定轴转动刚体惯性力系简化的主矢和主矩结果，其大小为FI= mac ; MIO=JOα。 -
第7题：
如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统对转轴O之动量矩为：
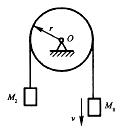答案：C解析：提示 根据动量矩定义和公式:LO= MO(m1v) + MO(m2v)+JO轮w。 -
第8题：
质量为m,半径为R的均质圆盘，绕垂直于图面的水平轴O转动，其角速度为ω，在图4-78示瞬时，角加速度为零，盘心C在其最低位置，此时将圆盘的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（）。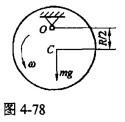
答案：A解析：提示：根据定轴转动刚体惯性力系简化的主矢和主矩结果，其大小FI=maC，MIO=JOα。 -
第9题：
如图4-65所示，忽略质量的细杆OC=l,其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是（ ）。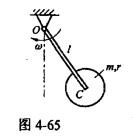
答案：D解析：提示：圆盘绕轴O作定轴转动，其动能为T=1/2JOω2。 -
第10题：
两个半径相同，均质等厚的铁圆盘和木圆盘，它们对通过质心且垂直于圆面的回转半径相同。
正确答案:错误 -
第11题：
单选题长为 的均质杆AD通过铰C、D与半径为 的均质圆盘固结成一体如图示。设该物体系统在图示平面内对A，B，C，D各点的转动惯量分别为JA丶JB、JC、JD，则（）。AJA最大
BJB最大
CJC最大
DJD最大
正确答案： C解析： 暂无解析 -
第12题：
均质圆盘质量为m，半径为R，在铅垂平面内绕O轴转动，图示瞬时角速度为ω，则其对O轴的动量矩和动能大小分别为：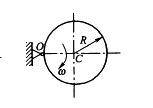
答案：D解析：
-
第13题：
图示a)、b)系统中的均质圆盘质量、半径均相同，角速度与角加速度分别为ω1、 ω2 和 α1、α2，则有:
A. α1 =α2
B. α1 >α2
C. α1 2
D. ω1 =ω2答案：B解析：提示：根据动量矩定理。 -
第14题：
图示均质杆AB的质量为m，长度为L，且O1A = O2B=R，O1O2=AB=L。当φ=60°时，O1A杆绕O1轴转动的角速度为ω，角加速度为α，此时均质杆AB的惯性力系向其质心C简化的主矢FI和主矩MIC的大小分别为：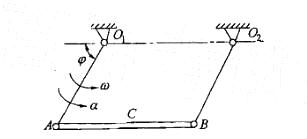
A. FI=mRα ,MIC=1/3mL2α B. FI=mRω2 ,MIC = 0
答案：C解析：提示:AB是平动刚体。 -
第15题：
图示均质杆AB的质量为m，长度为L，且O1A = O2B=R，O1O2=AB=L。当φ=60°时，O1A杆绕O1轴转动的角速度为ω，角加速度为α，此时均质杆AB的惯性力系向其质心C简化的主矢FI和主矩MIC的大小分别为：
A. FI=mRα ,MI
B=1/3mL2α
C. FI=mRω2 ,MI
D = 0
答案：C解析：提示：AB是平动刚体。 -
第16题：
如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统的动量为：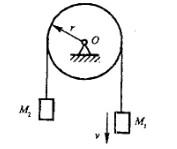
答案：B解析：提示:根据动量的定义p=∑mivi。 -
第17题：
圆盘某瞬时以角速度ω，角加速度α绕O轴转动，其上A、B两点的加速度分别为aA和aB，与半径的夹角分别为θ和φ。若OA=R，OB=R/2，则aA与aB，θ与φ的关系分别为：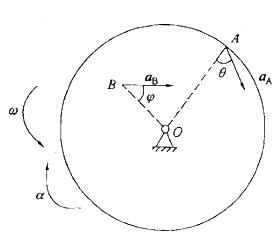
A.aA=aB,θ=φ
B. aA=aB,θ=2φ
C. aA=2aB,θ=φ
D. aA=2aB,θ=2φ答案：C解析：提示：定轴转动问题，aA = anA+aτA，aAn= Rω2，aAτ=Rα，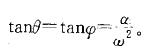
-
第18题：
如图4-59所示(1)、(2)系统中的均质圆盘质量、半径均相同，角速度与角加速度分别为ω1、ω2和α1、α2,则有（ ）。
A. α1=α2 B. α1>α2 C. α12 D. ω1=ω2答案：B解析：提示：根据动量矩定理。 -
第19题：
如图4-72所示，质量为m1的均质杆OA, 一端较接在质量为m2的均质圆盘中心， 另一端放在水平面上，圆盘在地面上作纯滚动。圆心速度为v,则系统的动能为（ ）。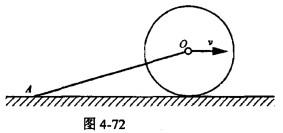
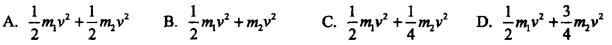答案：D解析：提示：杆OA平行移动，轮O作平面运动，分别根据动能的定义求解。 -
第20题：
如图4-45所示，圆盘某瞬时以角速度ω，角加速度α绕轴O转动，其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R, OB = R/2,则aA与aB，θ与 φ 的关系分别为（ ）。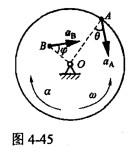
A.aA=aB θ=φ B.aA=aB θ=2φ C.aA=2aB θ=φ D.aA=2aB θ=2φ答案：C解析：提示：定轴转动刚体内各点加速度的分布为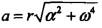
,其中r为点到转动轴的距离;
。 -
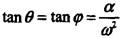第21题：
单选题图4-3-1所示均质链条传动机构的大齿轮以角速度ω转动，已知大齿轮半径为R，质量为m1，小齿轮半径为r，质量为m2，链条质量不计，则此系统的动量为（ ）。[2014年真题]图4-3-1A（m1+2m2）v（→）
B（m1+m2）v（→）
C（2m2-m1）v（→）
D0
正确答案： C解析： 动量是指物体的质量与其运动速度的乘积，是物体机械运动强弱的一种度量。本题中，两齿轮质心速度vC＝0，故系统动量为0。