假设一个消费者的效用函数为u= xy+y，其中z和y分别表示两种商品。 (1)请问此效用函数是拟凹的吗？ (2)计算均衡需求函数和马歇尔需求函数。 (3)计算间接效用函数和支出函数。

第1题：

答案：

解析：

(3)间接效用函数衡量的是在收入和价格一定的情况下，消费者选择最优消费束时的效用。将(2)中所求的马歇尔需求函数代入原效用函数中，可得间接效用函数为：

支出函数是指在一组特定的商品价格条件下，要达到某一既定的效用水平所必需的最小支出，与 间接效用函数互为反函数，可得支出函数为：

第2题：

假定某消费者的效用函数为

两商品的价格分别为P1、P2，消费者的收入为M。求该消费者关于商品1和商品2的需求函数。

答案：

解析：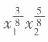

第3题：

答案：

解析：

求解消费者效用最大化时要满足：

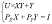
通过构造拉格朗日辅助函数得：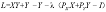

求得其一阶导数为并令其为0：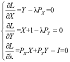

得： X的需求函数为：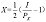

Y的需求函数为：

第4题：

第5题：

第6题：

考虑一个两人两商品的交换经济，A和B均只消费商品x和y。A的效用函数为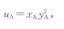

B的效用函数为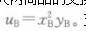

交换前，A有9单位x和0单位y;B有0单位x和6单位y。(1)写出A和B的边际替代

(2)求契约曲线方程。(3)求此交换经济的一般均衡。

答案：

解析：

(1)由消费者A的效用函数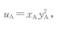

则消费者A的边际替代率为：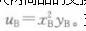

同理可得，消费者B的边际替代率为：

(2)一般均衡时有

则有: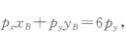


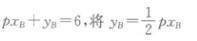
此即为契约曲线方程。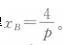

对于消费者A来说，其预算约束为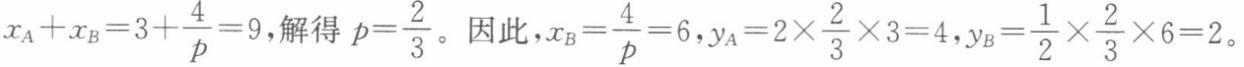

第7题：

假设在一个2×2的交换经济中消费者A和B交换两种商品z和y，消费者A的效用函数 是UA (XA，yA)=

，消费者B的效用函数是ub（xb，yB）=

他们拥有两种商品的初始 禀赋分别是WA(40，60)和WB(40，40)。标准化商品x的价格Px=1，商品y的价格为P。 (1)计算消费者A和B对两种商品z和y的需求函数。 (2)计算该交换经济的均衡价格及均衡配置。

答案：

解析：

(1)消费者A、B各自的收入为40+60P、40+40P。 由柯布一道格拉斯效用函数的性质可知A的需求函数为：

B的需求函数为：

(2)联立消费者A、B关于商品z的需求函数可得： xA+xB =40+50P=80 解得：P=4/5 可得：xA =44，yA =55，XB =36，yB=45。

第8题：

答案：

解析：

消费者的效用最大化问题为：

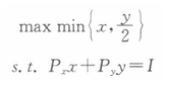
由(1)可知，消费者效用最大化的必要条件为，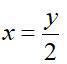

代入Pxx+Pyy=I，可得两种物品的消费函数分别为：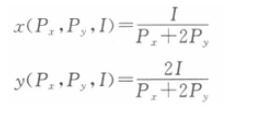

第9题：

假设消费者张某对X和Y两种商品的效用函数为U=X₂Y₂，张某收入为500元，X和Y的价格分别为P_x=2元，P_y=5元，求：张某对X和Y两种商品的最佳组合。

第10题：

I=Px•X+Py•Y是消费者的（）

• A、需求函数
• B、效用函数
• C、预算约束方程
• D、不确定

第11题：

第12题：

第13题：

某人的效用函数为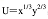

收入为m，其中x和y的价格分别为p1，p2。 求出消费者均衡时，该人对x，y两商品的需求函数。

答案：

解析：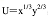

第14题：

第15题：

答案：

解析：

第16题：

答案：

解析：

综上，消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。

第17题：

设某消费者的效用函数为柯布一道格拉斯类型的，即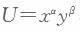

商品x和商品y的价格分别为

消费者的收人为M，a和β为常数，且a+ β=1。 (1)求该消费者关于商品X和商品y的需求函数。 (2)证明当商品X和商品y的价格以及消费者的收入同时变动一个比例时，消费者对两商品的需求关系维持不变。 (3)证明消费者效用函数中的参数a和β分别为商品x和商品y的消费支出占消费者收入的份额。

答案：

解析：

第18题：

答案：

解析：

第19题：

答案：

解析：

第20题：

某人的效用函数为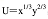

收入为m，其中x和y的价格分别为p1，p2。求该消费者的间接效用函数。

答案：

解析：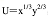

第21题：

效用函数的基本类型（）。

• A、凹性效用函数
• B、凸性效用函数
• C、线性效用函数
• D、多元效用函数

第22题：

计算题：假设消费者张某对X和Y两种商品的效用函数为U=X₂Y₂，张某收入为500元，X和Y的价格分别为P_X=2元，P_Y=5元，求：张某对X和Y两种商品的最佳组合。

第23题：