在只有两个参与人且每个参与人都只有两个策略可供选择的情况下，纯策略的纳什均衡最多可有几个？为什么？

题目
在只有两个参与人且每个参与人都只有两个策略可供选择的情况下，纯策略的纳什均衡最多可有几个？为什么？

相似考题

1.下列有关纳什均衡定义正确的是（）.A.当参与的一方拥有一种战略，该战略无论何时，无论其他参与者选择什么战略，都优于它可选择的其他战略。B.假设有两个或两个以上的参与人参与博弈，给定其他参与人策略的条件下，每个参与人选择自己的最优策略，所有参与人选择的策略一起构成一个策略组合。C.达到纳什均衡时，参与者所采取的策略是使自己能够获得最大收益。D.达到纳什均衡时，参与者收益满足最小收入最大化。

2.有关子博弈精炼纳什均衡说法错误的是（）.A.要求某一策略组合在每一个子博弈上都构成一个纳什均衡B.也是一个一般意义上的纳什均衡C.和纳什均衡没有关系D.要求某一策略组合在原博弈上都构成一个纳什均衡

3.纳什均衡的理解()。A、是一种优势策略B、是一种对各方来说最优的策略集合C、在一策略集合中，每个竞争者在确信对手所采取的策略情况下，选择自己的最佳策略D、一种下策

4.下列有关策略和纳什均衡的叙述错误的是（）.A.混合策略是博弈方根据一组选定的概率，在两种或两种以上可能的行为中随机选择的策略B.纯策略是博弈方采取一种选择或一种行动C.有些博弈不存在纯策略纳什均衡，但存在混合策略的纳什均衡D.有些博弈存在纯策略纳什均衡，但也存在混合策略的纳什均衡

更多“在只有两个参与人且每个参与人都只有两个策略可供选择的情况下，纯策略的纳什均衡最多可有几个？为什么？”相关问题

  • 第1题：

    纳什均衡是指这样一种状态，若所有其他参与人的策略都不变的话，我无论再选择其它什么策略得到的得益不会比我选择现在的策略得到的得益大。()


    参考答案：正确

  • 第2题：

    两个寡头厂商在进行博弈竞争，他们的策略及支付矩阵如下，则( )。

    A.甲厂商有占优策略
    B.乙厂商没有占优策略
    C.（中，中）是纳什均衡
    D.没有纳什均衡

    答案：C
    解析：
    根据上述支付矩阵，不论甲选择“上”、“中”、“下”，对于乙来说选择“中”是占优策略；如果乙选择“左”，则甲会选择“下”；如果乙选择“中”，则甲会选择“中”；如果乙选择“右”，则甲会选择“中”。所以，对于甲、乙来说，（中，中）是一组纳什均衡。

  • 第3题：

    在一条狭窄的巷子里，两个年轻人骑着自行车相向而行，每个人都有两个策略，即或者选择“冲过去”，或者选择“避让”。如果选择“避让”，不管对方采取什么策略，他得到的收益都是0；如果一人采取“冲过去”的战略，那么如果对方采取“避让”，他得到的收益是9；如果对方“不避让”，他得到的收益是-36。这个博弈有两个纯策略纳什均衡和( )。

    A.一个混合策略纳什均衡，即两个人都以80%的概率选择“避让”，以20%的概率选择“冲过去”
    B.一个混合策略纳什均衡，即一个人以20%的概率选择“避让”，另一个人以80%的概率选择“冲过去”
    C.一个混合策略纳什均衡，即两个人都以40%的概率选择“避让”，以60%的概率选择“冲过去”
    D.没有混合策略纳什均衡

    答案：A
    解析：
    假定两个年轻人分别为A，B，两者策略的支付矩阵如下表所示：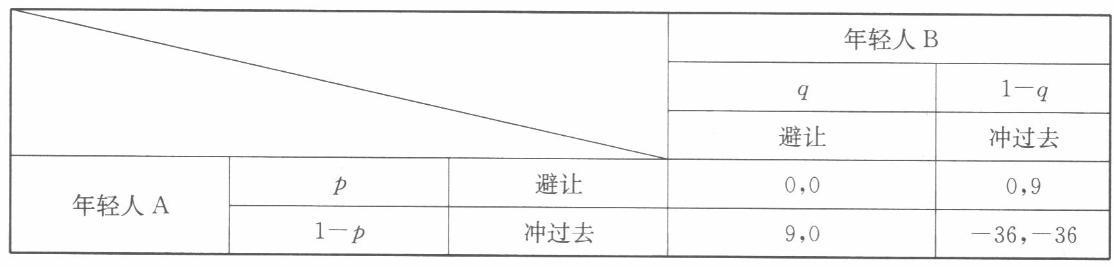

    假定年轻人A和B选择避让的概率为p和q，根据等支付原则有：p×0+(1-p)×0=p×9+(1-p)×（-36) q×0+(1-q)×0=q×9+(1-q)×（-36) 解得：p=q= 80%。故存在一个混合策略纳什均衡，两个人都以80%的概率选择“避让”，以20%的概率选择“冲过去”。

  • 第4题：

    设某个纯策略博弈的纳什均衡是有限的一试问：相应的混合策略博弈的纳什均衡会是无限的吗？试举一例说明：


    答案：
    解析：
    会存在，如表10-8所示。

  • 第5题：

    在只有两个参与人且每个参与人都只有两个策略可供选择的情况下，纯策略的纳什均衡司能有三个，试举一例说明


    答案：
    解析：
    如表10—5所示。

  • 第6题：

    子博弈精炼纳什均衡（）。

    • A、是一个一般意义上的纳什均衡；
    • B、和纳什均衡没有什么关系；
    • C、要求某一策略组合在每一个子博弈上都构成一个纳什均衡；
    • D、要求某一策略组合在原博弈上都构成一个纳什均衡。

    正确答案:C

  • 第7题：

    有关子博弈精炼纳什均衡说法错误的是（）.

    • A、要求某一策略组合在每一个子博弈上都构成一个纳什均衡
    • B、也是一个一般意义上的纳什均衡
    • C、和纳什均衡没有关系
    • D、要求某一策略组合在原博弈上都构成一个纳什均衡

    正确答案:C

  • 第8题：

    下列有关古诺模型说法错误的是？（）

    • A、古诺寡头竞争模型是纳什均衡最早的版本，比纳什的定义早了100多年
    • B、在古诺模型中，两个参与人进行的是价格竞争
    • C、由法国经济学家古诺在1838年首先提出来的
    • D、在古诺模型中，有两个参与人，战略是选择产量

    正确答案:B

  • 第9题：

    在博弈论中，占优策略均衡总是纳什均衡吗？纳什均衡一定是占优策略均衡吗？


    正确答案:占优策略均衡总是纳什均衡，而纳什均衡不一定是占优策略均衡。占有策略均衡是指博弈中所有参与者都不改变自己策略的一种状态。由博弈中所以参与者的占优策略（无论其他参与者采取什么策略，参与者的唯一最优策略就是他的占优策略）所组成的均衡就是占优策略均衡，而给其他参与者策略条件下每个参与者所选择的最优策略所构成的策略组合则是纳什均衡。显然占优策略均衡是纳什均衡的一种特殊情况。在这种情况下，不管其他参与者采取何种策略，本参与者所采取的策略总是要优于别的策略。而在纳什均衡中，只要对手策略给定的情况下，本策略者的策略最优即可。

  • 第10题：

    在只有两个参与人且每个参与人都只有两个策略可供选择的情况下，如何找到所有的纯策略纳什均衡？


    正确答案:可使用条件策略下划线法。具体步骤如下：首先，设两个参与人分别为左参与人和上参与人，并把整个的支付矩阵分解为这两个参与人的支付矩阵；其次，在左参与人的支付矩阵中，找出每一列的最大者，并在其下划线；再次，在上参与人的支付矩阵中，找出每一行的最大者，并在其下划线；再再次，将已经划好线的两个参与人的支付矩阵再合并起来，得到带有下划线的整个支付矩阵；最后，在带有下划线的整个支付矩阵中，找到两个数字之下均划有线的所有的支付组合。这些支付组合所代表的策略组合就是纳什均衡。

  • 第11题：

    纳什均衡发生于以下哪种情况时（）

    • A、两个参与人选择同样的策略
    • B、一个参与人选择了最优策略
    • C、参与人都没选择最优策略
    • D、给定其他参与人策略的情况下，每个参与人选择其最优的策略

    正确答案:D

  • 第12题：

    单选题
    关于纳什均衡，下列说法错误的是（　　）。
    A

    在囚徒困境中有且只有一个纳什均衡

    B

    指一种策略组合，使得同一时间内每个参与人的策略是对其他参与人策略的最优反应

    C

    给定别人策略的情况下，没有任何单个参与人有积极性选择其他策略，从而没有任何人打破这种均衡

    D

    指这样一种均衡，局中每个人都选择其占优策略


    正确答案： D
    解析：
    纳什均衡，是指参与人的这样一种策略组合，在该策略组合上，任何参与人单独改变策略都不会得到好处。如果存在占优策略的话，应该选择占优策略，因为占优策略是与他人选择无关的最优策略。

  • 第13题：

    在纳什均衡中，()。

    A.每个人都选择自己的最优策略
    B.给定他人的选择，每个人都不会改变策略
    C.均衡的策略是可以自动实施的
    D.以三种说法上都对

    答案：B
    解析：
    所谓纳什均衡，指的是参与人的这样一种策略组合，在该策略组合上，任何参与人单独改变策略都不会得到好处。或者换个说法：如果在一个策略组合上，当所有其他人都不改变策略时，没有人会改变自己的策略，则该策略组合就是一个纳什均衡，故B项正确、ACD错误。所以答案选B。

  • 第14题：

    设某个纯策略博弈的纳什均衡不存在试问：相应的混合策略博弈的纳什均衡会存在吗？试举一例说明．


    答案：
    解析：
    在同时博弈中，纯策略的纳什均衡可能存在，也可能不存在，但相应的}昆合策略纳什均衡总是存在的。例如表10-9所示，在下面的二人同时博弈中，根据条件策略下划线法可知由于没有一个单元格中两个数字之下均有下划线，故纯策略的纳什均衡不存在，但是相应的混合策略纳什均衡却是存在的。

    首先分别计算甲厂商和乙厂商的混合策略： E甲=4P1ql+9P1(1-ql)+7(1-P1)ql+2(1-P1)(1-q1) =p1(7 -1Oql) +5q1 +2 E乙= 6P1ql+P1(1- q1)+3(1-p1)ql+8(1- P1)(1- q1) =5q1(2p1 -1) -7P1+8 其次分别计算甲厂商和乙厂商的条件混合策略：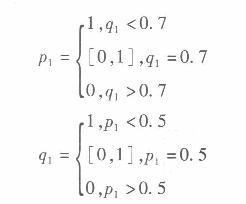

    最后，混合策略纳什均衡参见图10-1中点e，此时混合策略纳什均衡可以表示为： ((P1,p2)(q1,q2))=((0.5,0.5)(0.7,0.3)) 但不存在纯策略博弈的纳什均衡。

  • 第15题：

    根据表10 -11的二人同时博弈模型，求： (1)参与人A与B的期望支付。 (2)参与人A与B的条件混合策略。 (3)纳什均衡。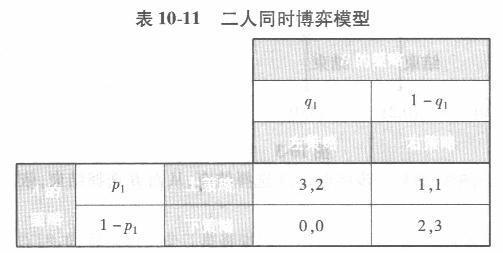


    答案：
    解析：
    (1)由划线法可知参与人A与B的期望支付为： EA =3P1q1 +P1(1- q1)+2(1-P1)(1- q1) =4P1q1 -2q1 -P1 +2 =Pl (4q1 -1)- 2q1+2 EB =2P1q1 +P1(1- q1)+3(1-P1)(1- q1) =4P1q1 -2p1 -3q1 +3 =q1(4p1 -3)- 2p1+3 (2)参与人A与B的条件混合策略为：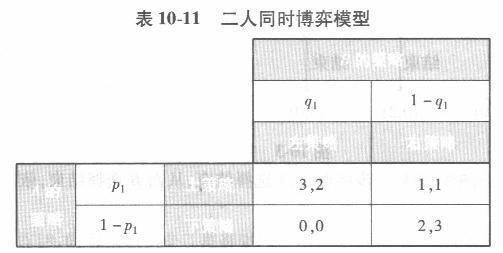

    (3)纯策略纳什均衡为(3，2)(2，3)，即（上，左）（下，右），混合策略纳什均衡为(3/4上，1/4左)如图10-5所示。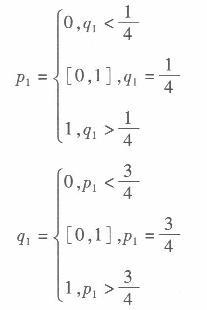

  • 第16题：

    根据表10-12是二人同时博弈模型，求： (1)参与人A与B的期望支付。 (2)参与人A与B的条件混合策略。 (3)纳什均衡。


    答案：
    解析：
    (1)参与人A与B的期望支付为： EA =3P1q1 +2p1(1- q1) +3(1一pl)g1+(1-P1)(1-q1) = -P1q1 +P1 +2q1 +1 =p1(l -q1) +2q1 +1 EB=p1(1- q1) +2(1 -P1)q1+(1-P1)(1- q1) = -2P1q1 +q1 +1 =q1(l -2p1) +1 (2)参与人A与B的条件混合策略：

    (3)纯策略纳什均衡为(2，1)(3，2)，即（上，右）（下，左），混合策略纳什均衡为（1/2上，1/2左），如图10-6所示。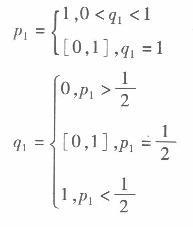

  • 第17题：

    在只有两个参与人且每个参与人都有三个策略可供选择的情况下，纯策略的纳什均衡最多可有几个？


    答案：
    解析：
    纯策略的纳什均衡最多有9个，因为每个人都有三个策略可供选择，故会出现9种支付。结果，故最多可有9个。

  • 第18题：

    纳什均衡即任一博弈方单独改变策略都只能得到更小利益的策略组合。


    正确答案:正确

  • 第19题：

    猎鹿博弈中存在三个纯策略的纳什均衡。


    正确答案:错误

  • 第20题：

    关于纳什均衡的说法中，如下正确的是（）

    • A、在某些博弈中，可能就根本不存在纯策略的纳什均衡
    • B、纳什均衡可能是有效率的也有可能是无效率的
    • C、根据纳什均衡的定义，纳什均衡都是有效率的
    • D、纳什均衡不可能存在着多重均衡

    正确答案:A,B

  • 第21题：

    混合策略纳什均衡与纯策略纳什均衡有什么不同？


    正确答案:在纯策略博弈中，纳什均衡是参与人的一种策略组合，在该策略组合上，任何参与人单独改变其策略都不会得到好处；在混合策略博弈中，纳什均衡是参与人的一种概率向量组合，在该概率向量组合上，任何参与人单独改变其概率向量都不会得到好处。

  • 第22题：

    设某个纯策略博弈的纳什均衡是有限的。试问：相应的混合策略博弈的纳什均衡会是无限的吗？试举一例说明。


    正确答案:当纯策略博弈的纳什均衡为有限时，相应的混合策略博弈的纳什均衡既可能是有限的，也可能是无限的。例如，在只包括A与B的二人同时博弈中，混合策略纳什均衡的“集合”可以是单位平面、三条线段、两条线段、一条线段、三个点、两个点和一个点，其中，前四种情况就意味着存在无限多个纳什均衡。

  • 第23题：

    多选题
    纳什均衡的理解（）
    A

    是一种优势策略

    B

    是一种对各方来说最优的策略集合

    C

    在一策略集合中，每个竞争者在确信对手所采取的策略情况下，选择自己的最佳策略

    D

    一种下策


    正确答案： D,B
    解析： 暂无解析

相关内容