已知劳动是唯一的可变要素，生产函数为Q =A +10L - 5L2，产品市场是完全竞争的，劳动价格为W．试说明： (1)厂商为劳动的需求函数。 (2)厂商对劳动的需求量与工资反方向变化。 (3)厂商对劳动的需求量与产品价格同方向变化：
题目
已知劳动是唯一的可变要素，生产函数为Q =A +10L - 5L2，产品市场是完全竞争的，劳动价格为W．试说明： (1)厂商为劳动的需求函数。 (2)厂商对劳动的需求量与工资反方向变化。 (3)厂商对劳动的需求量与产品价格同方向变化：
相似考题
更多“ 已知劳动是唯一的可变要素，生产函数为Q =A +10L - 5L2，产品市场是完全竞争的，劳动价格为W．试说明： (1)厂商为劳动的需求函数。 (2)厂商对劳动的需求量与工资反方向变化。 (3)厂商对劳动的需求量与产品价格同方向变化：”相关问题
-
第1题：
已知某个完全竞争行业中的单个厂商的短期成本函数是STC=0.1Q3—2Q2+15Q+10。求：
(1)当市场上产品的价格为P=55时，厂商的短期均衡产量和利润;
(2)当市场价格下降为多少时，厂商必须停产;
(3)厂商的短期供给函数。
答案：
解：(1)已知STC=0.1Q3 - 2Q2+15Q+10，P=55
完全竞争厂商的短期均衡的条件是：P=MR=SMC
SMC=dSTC/dQ=0.3Q2 - 4Q+15
当P=55，即55=0.3Q2 - 4Q+15
解方程得Q=20
即短期均衡产量为20。利润等于总收益减总成本，
即л=TR-TC=P×Q – (0.1Q3– 2Q2+15Q+10)
将P=55，Q=20代入求得：л=790
即厂商的短期均衡产量和利润分别为20和790。
(2)厂商必须停产的条件是：价格等于AVC的最小值。
因为TC=VC+FC，FC=10，
所以VC=0.1Q3 -2Q2+15Q
AVC=VC/Q=0.1Q2 -2Q+15;对Q求导，令dAVC/dQ=0，可得：dAVC/dQ=0.2Q-2=0，求得Q=10, 即当Q=10，AVC取最小值;此时，AVC=10-20+15=5
也就是说，当价格下降到5时，厂商必须停产。
(3)厂商的短期供给函数用SMC曲线大于和等于停止营业点的部分来表示。相应的，厂商的短期供给函数应该就是SMC函数，即SMC=dSTC/dQ=0.3Q2 - 4Q+15，但要满足Q10即大于停止营止点的产量。
-
第2题：
关于工资率变化与劳动力需求量之间关系的说法，正确的有()。A:工资率变化对劳动力需求量不会产生影响
B:工资率变化会对劳动力需求量产生规模效应
C:工资率变化会对劳动力需求量产生替代效应
D:其他条件一定，工资率与劳动力需求量呈同方向变化
E:其他条件一定，工资率与劳动力需求量呈反方向变化答案：B,C,E解析：选项A，从宏观角度来说，劳动力需求是指在一定的市场工资率下，各行业的劳动力需求量总和，从微观的角度来看，则是指在一定的市场工资率水平上，企业所需要的某种既定质量的劳动力的数量。选项D，在其他条件不变的情况下，工资率变动所产生的规模效应和替代效应的作用方向都是相同的，即工资率上升的规模效应导致劳动力需求量下降，其替代效应也导致劳动力需求量下降；而工资率下降的规模效应导致劳动力需求量上升，其替代效应也导致劳动力需求量上升。 -
第3题：
假定某垄断厂商生产一种产品，其总成本函数为TC=0.SQ2 +10Q +5，市场的反需求函数为P=70 -2Q： (1)求该厂商实现利润最大化时的产量、产品价格和利润量。 (2)如果要求该垄断厂商遵从完全竞争原则，那么，该厂商实现利润最大化时的产量、产品价格和利润量又是多少？ (3)试比较(1)和(2)的结果，你可以得出什么结论？答案：解析：(1)厂商边际成本函数为MC=Q+10， 边际收益函数为MR =70 -4Q。 根据利润最大化原则MR =MC， 可知Q =12，P=46，利润π=PQ - TC= 355。 (2)根据完全竞争原则可知P=MC， 可得Q =20，P=30， 此时利润π= PQ - TC= 195。 (3)比较(1)和(2)可知，垄断条件下的利润更大，价格更高，但产量却比较低。 -
第4题：
已知一个厂商的生产函数Q=1/11（4KL - L2一K2），其中K和L分别表示资本和劳动，且要素市场价格分别为v和ω。产品的市场价格为P，而该企业仅是一个价格接受者。假设该厂商产品的市场需求函数Q=a-0.5P。若劳动力市场是完全竞争的，求该厂商对劳动的需求函数。答案：解析：
-
第5题：
完全竞争市场上，厂商生产要素为x1，x2，面对的是竞争性要素需求市场，两种要素的价格都为2，每个企业的固定成本为64。单个厂商的生产函数为
消费者对该产品的需求函数为Q=280-5p，其中p为产品的市场价格 长期均衡时候企业个数答案：解析：当价格为32时，市场的总需求Q=280-160=120。而单个厂商产量为4，故长期均衡时，企业个数为30个。 -
第6题：
完全竞争行中某厂商的成本函数为TC=Q3-6Q2+30Q+40试求： (1)假设产品价格为66元，利润最大化时的产量及利润总额。 (2)竞争市场供求发生变化，由此决定的新价格为30元，在新价格下，厂商是否会发生亏损？如果会，最小的亏损额为多少？ (3)该厂商在什么情况下会停止生产？ (4)厂商的短期供给函数。答案：解析：
-
第7题：
设一厂商使用的可变要素为劳动L，其生产函数为Q= -O. O1L3+L2+38L 其中，Q为每日产量，L为每日投入的劳动小时数，所有市场（劳动市场及产品市场）都是完全竞争的，单位产品价格为0. 10美元，小时工资为5美元，厂商要求利润最大化。问厂商每天雇用多少小时的劳动？答案：解析：已知工资W=5，根据生产函数及产品价格P=0.10，可求得劳动的边际产品价值如下：
-
第8题：
已知某完全竞争行业中的单个厂商的短期成本函数为STC＝0.1Q3—2Q2+15Q+10。试求：（1）当市场上产品的价格为P=55时，厂商的短期均衡产量和利润；（2）当市场价格下降为多少时，厂商必须停产；（3）厂商的短期供给函数。
正确答案: （1）P=MR=55
短期均衡时SMC=0.3Q2-4Q+15=MR=55
0.3Q2-4Q-40=0
∴Q=20或Q=-20/3（舍去）
利润=PQ-STC=55×20-（0.1×8000-2×400+15×20+10）=790
（2）厂商停产时，P=AVC最低点。
AVC=SVC/Q=（0.1Q3—2Q2+15Q）/Q=0.1Q2-2Q+15
AVC最低点时，AVC′=0.2Q-2=0
∴Q=10
此时AVC=P=0.1×100-2×10+15=5
（3）短期供给函数为P=MC=0.3Q2-4Q+15（取P＞5一段） -
第9题：
已知生产函数Q=f（L，K）=4KL-L2-0.25K2，假定厂商目前处于短期生产，且K=20。 （1）写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。 （2）分别计算当劳动的总产量TPL、劳动的平均产量APL和劳动的边际产量MPL各自达到极大值时的厂商的劳动投入量。 （3）什么时候APL=MPL？它的值又是多少？
正确答案:（1）由生产函数数Q=4KL-L2-0.25K2，且K=20，可得短期生产函数为：Q=80L-L2-0.25*202=80L-L2-100，于是，根据总产量、平均产量和边际产量的定义，有以下函数： 劳动的总产量函数TPL=80L-L2-100，劳动的平均产量函数APL=80-L-100/L，劳动的边际产量函数MPL=80-2L。
（2）关于总产量的最大值：80-2L=0解得L=40，所以，劳动投入量为40时，总产量达到极大值。关于平均产量的最大值：-1+100L-2=0，L=10（负值舍去），所以，劳动投入量为10时，平均产量达到极大值。关于边际产量的最大值：由劳动的边际产量函数MPL=80-2L可知，边际产量曲线是一条斜率为负的直线。考虑到劳动投入量总是非负的，所以，L=0时，劳动的边际产量达到极大值。
（3）当劳动的平均产量达到最大值时，一定有APL=MPL。由（2）可知，当劳动为10时，劳动的平均产量APL达最大值，及相应的最大值为：APL的最大值=60，MPL=80-20=60，很显然APL=MPL=60。 -
第10题：
问答题计算题： 已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3－2Q2＋15Q+10。试求： （1）当市场上产品的价格为P=55时，厂商的短期均衡产量和利润； （2）当市场上价格下降为多少时，厂商必须停产； （3）厂商的短期供给函数正确答案： （1）根据MC=MR=P
MC=dSTC/dQ=0.3Q2－4Q+15=55=P
解得Q=20
利润=TR－STC=55*20－（0.1*203－2*202＋15*20+10）=790
（2）停业点为AVC的最低点
AVC=TVC/Q=0.1Q2－2Q＋15
当Q=10时AVC最小且AVC=5所以P=5时厂商必须停产
（3）短期供给函数即SMC函数且大于最低AVC对应产量以上的区间
SMC=dSTC/dQ=0.3Q2－4Q+15
所以短期供函数为0.3Q2－4Q+15（Q≥10）解析： 暂无解析 -
第11题：
问答题已知某完全竞争行业中的单个厂商的短期成本函数为STC＝0.1Q3—2Q2+15Q+10。试求：（1）当市场上产品的价格为P=55时，厂商的短期均衡产量和利润；（2）当市场价格下降为多少时，厂商必须停产；（3）厂商的短期供给函数。正确答案： （1）P=MR=55
短期均衡时SMC=0.3Q2-4Q+15=MR=55
0.3Q2-4Q-40=0
∴Q=20或Q=-20/3（舍去）
利润=PQ-STC=55×20-（0.1×8000-2×400+15×20+10）=790
（2）厂商停产时，P=AVC最低点。
AVC=SVC/Q=（0.1Q3—2Q2+15Q）/Q=0.1Q2-2Q+15
AVC最低点时，AVC′=0.2Q-2=0
∴Q=10
此时AVC=P=0.1×100-2×10+15=5
（3）短期供给函数为P=MC=0.3Q2-4Q+15（取P＞5一段）解析： 暂无解析 -
第12题：
问答题已知某完全竞争行业中的单个厂商的短期成本函数为：STC=0.1Q3-2Q2+15Q+10（1）当市场上产品价格为 55时厂商的短期均衡产量和利润；（2）当市场价格下降为多少时厂商必须停产？（3）求厂商的短期供给函数。正确答案：
由短期成本函数可得厂商的短期边际成本函数为:SMC=0.3Q2-4Q+15。
完全竞争厂商实现短期均衡时,有SMC=P,即0.3Q2-4Q+15=55,解得:Q=20。
此时,利润为π=PQ-STC=55×20-(0.1×203-2×202+15×20+10)=790。
即均衡产量为20,利润为790。解析： 暂无解析 -
第13题：
关于工资率变化与劳动力需求量之间的关系的说法，正确的是()。A:工资率变化对劳动力需求量不会产生影响
B:工资率变化会对劳动力需求量产生规模效应
C:工资率变化会对劳动力需求量产生替代效应
D:其他条件一定，工资率与劳动力需求量呈同方向变化
E:其他条件一定，工资率与劳动力需求量呈反方向变化答案：B,C,E解析：工资率的变化是通过规模效应和替代效应两个方面的作用对劳动力需求的数量产生影响的。在其他条件不变的情况下，工资率上升的规模效应导致劳动力需求量下降，其替代效应也导致劳动力需求量下降；而工资率下降的规模效应导致劳动力需求量上升，其替代效应也导致劳动力需求量上升。 -
第14题：
垄断厂商生产某一产品，产品的成本函数为C(q)=q2，市场反需求函数为p=120-q。试求：(1)垄断厂商利润最大化的产量和价格，并画图说明。(2)政府对垄断厂商征收100元的税收后，垄断厂商的产量和价格。(3)政府对垄断厂商单位产品征收从量税2元，垄断厂商的产量和价格。答案：解析：(1)垄断厂商的边际成本函数为MC= 2q，边际收益函数为MR =120 - 2q，根据垄断 厂商利润最大化原则MR =MC，可以解得垄断厂商利润最大化的产量和价格分别为q*一30、 p* =90。如图1 2所示，厂商在MR曲线和MC曲线的交点处确定利润最大化的产量q* =30， 再根据q’对应的市场需求曲线D上的点确定产品的价格p* =90。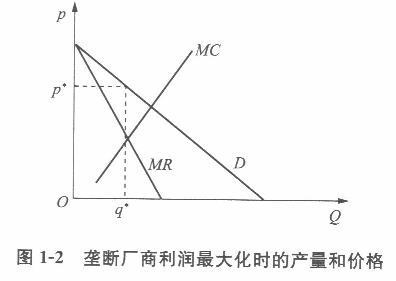
(2)当政府对垄断厂商征收100元税收后，垄断厂商的实际成本函数变为： C(q) =q2+100 但垄断厂商的边际成本函数仍为MC=2q，因而利润最大化的条件不变，因此垄断厂商利润最大 化的产量和价格仍然为q+ =30、p* =90。 (3)当政府对垄断厂商单位产品征收从量税2元后，垄断厂商的实际成本函数变为C(q)一qz+ 2q，边际成本函数则为MC=2q+2，边际收益函数仍为MR =120-2q，根据垄断厂商利润最大 化原则MR =MC，可以解得垄断厂商利润最大化的产量和价格分别为g’=29.5，p* =90.5。 -
第15题：
已知生产函数Q=f（L,K）=2KL-0.5L2-0.5K2，假定厂商目前处于短期生产切K的平均数为10 (1)写出在短期生产中该厂商关于劳动的总产量TPL函数、关于劳动的平均产量APL函数和关于劳动的边际产量MPL函数。 (2)分别计算当劳动的总产量TPL、劳动的平均产量APL和劳动的边际产量MPL各自达到最大值时的厂商的劳动投入量。 (3)什么时候APL= MPL?它的值又是多少？答案：解析：
-
第16题：
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数为LTC= Q3 - 12Q2+40Q。试求： (1)当市场产品价格为P=100时，厂商实现MR= LMC时的产量、平均成本和利润。 (2)该行业长期均衡时的价格和单个厂商的产量。 (3)当市场的需求函数为Q=660 -15P时，行业长期均衡时的厂商数量。答案：解析：
故Q=6是长期平均成本最小化的解。 以Q=6代入LAC( Q)，得平均成本的最小值为LAC =62 -12 x6+40 =4。 由于完全竞争行业长期均衡时的价格等于厂商的最小的长期平均成本，所以，该行业长期均衡时的价格P=4，单个厂商的产量Q=6。 (3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线，而且相应的市场长期均衡价格是固定的，它等于单个厂商的最低的长期平均成本，所以，本题的市场长期均衡价格固定为P=4。以P=4代入市场需求函数Q=660 -15P，便可以得到市场的长期均衡数量为Q=660 -15 x4= 600。 现已求得在市场实现长期均衡时，市场的均衡数量Q =600，单个厂商的均衡产量Q=6。于是，行业长期均衡时的厂商数量= 600÷6=100。 -
第17题：
假设某完全竞争行业有200个相同的企业，企业的短期成本函数为TC =0. 2Q2+Q+15，市场需求函数为Qp= 2475 - 95P，厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q，求： (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。答案：解析：(1)先求单个企业的供给函数：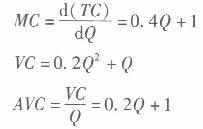
故A VC的最小值为1。 而MC的最小值也为1，故只有价格大于等于1，厂商才会供给商品。 此时单个企业的供给函数为P= MC =0.4Q +l，即Q=2.SP -2.5。 市场的供给函数为Qs=200Q =500P -500(P≥1)，由QD=QS可得P=5。 市场均衡产量为2000单位，每个厂商产量为10单位。 单个厂商利润为5 x10 - (0.2 x102 +10+15) =5。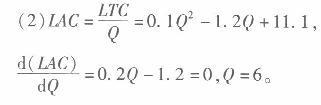
将Q=6代入LAC，得IAC =7.5。 由长期均衡条件可得P=7. 5. (3)将P=7.5代入需求函数可得市场需求量为1762.5，而200个厂商的供给量为1200，再加上厂商短期利润为正，长期利润为O，所以没有厂商退出经营。 -
第18题：
完全竞争市场上，厂商生产要素为x1，x2，面对的是竞争性要素需求市场，两种要素的价格都为2，每个企业的固定成本为64。单个厂商的生产函数为
消费者对该产品的需求函数为Q=280-5p，其中p为产品的市场价格 长期均衡时的单个企业产量和价格答案：解析：
-
第19题：
某企业生产一种产品，劳动为唯一可变要素，固定成本既定。短期生产函数Q=-0.1L3+6L22+12L，求： （1）劳动的平均产量函数和边际产量函数。 （2）企业雇用工人的合理范围是多少？ （3）若已知劳动的价格为W=480，产品Q的价格为40，则当利润最大时，企业生产多少产品Q？
（1）平均产量AP=TP/L= -0.1 L2 +6L+12 边际产量MP=（TP）’= - 0.3 L2+12L+12
（2）企业应在平均产量递减，边际产量为正的生产阶段组织生产，因此雇用工人的数量也应在此范围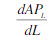
＜0，MP＞0内。 对APL求导，得
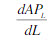= - 0.2 L +6=0。 即L=30
当L=30时，APL取得最大值，L＞30，APL开始递减。 令MPL= - 0.3L2+12L+12=0，得L=40.98
所以，企业雇用工人的合理范围为30≤L≤41
（3）利润π=PQ-WL=40（- 0.1 L3 +6L2 +12L）-480L = - 4 L3 +240L2 +480L-480L
Π’=- 12L2+480L，当Π’=0时， L=0 （舍去） 或L=40.
当L=40时， Π” ＜0，所以L=40,利润π最大。
此时，产量Q= -0.1×403+6 × 402 +12 × 40 =3680
略 -
第20题：
假设要素市场和商品市场完全竞争，生产要素只有劳动，某厂商在利润最大化的生产处劳动投入量为3个单位，产量为20，市场中的工资率为50，求商品的价格。
正确答案: ∵MPW*P*LW=Q*P
∴MPW=20/3MPW*P=W=50
∴P=50/MPW=50*3/20=7.5 -
第21题：
因为劳动的边际产品递减，因此只有降低工资率厂商才会增加劳动需求量，从而劳动需求曲线是负斜率的。
正确答案:正确 -
第22题：
问答题已知某厂商的生产函数为Q＝0.5L1/3K2/3；当资本投入量K＝50时资本的总价值为500；劳动的价格PL＝5。求： （1）劳动的投入函数L＝L（Q）； （2）总成本函数、平均成本函数和边际成本函数； （3）当产品的价格P＝100时，厂商获得最大利润的产量和利润各是多少？正确答案： (1)因为K=50,则Q=0.5L1/3K2/3=0.5L1/3502/3,L=0.0032Q3,此即为劳动的投入函数。
(2)总成本函数为:TC=PLL+PKK=0.016Q3+500
平均成本函数为:ATC=TC/Q=0.016Q2+500/Q
边际成本函数为:MC=dTC/dQ=0.048Q2
(3)当产品的价格P=100时,厂商的边际收益MR=P=100,由厂商获得最大利润的条件MR=MC,即100=0.048Q2,解得Q≈45.64。
此时利润:π=PQ-TC=100×45.64-0.016×45.643-500≈2543。解析： 暂无解析 -
第23题：
单选题设某一厂商的生产函数为：Q＝－0.1L3＋6L2＋12L（Q为每周产量，L为每周雇佣的劳动量），若产品、要素市场均完全竞争，产品价格为30元，周工资率为360元，厂商追求最大利润，则每周雇佣的劳动量是（ ）。A30
B40
C50
D20
E15
正确答案： D解析：
利润π＝PQ－C＝30×（－0.1L3＋6L2＋12L）－360L＝－3L3＋180L2。厂商利润最大化时，利润函数应当满足以下条件：dπ/dL＝－9L2＋360L＝0，解得：L＝40。即每周雇佣的劳动量为40时，厂商可以获得最大利润。
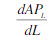＜0，MP＞0内。 对APL求导，得
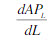= - 0.2 L +6=0。 即L=30