设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则A.AP{Y=-2X-1}=1 B.P{Y=2X-1}=1 C.P{Y=-2X+1}=1 D.P{Y=2X+1}=1

题目
设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则



A.AP{Y=-2X-1}=1
B.P{Y=2X-1}=1
C.P{Y=-2X+1}=1
D.P{Y=2X+1}=1
相似考题

1.设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为()A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布

2.设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则

3.设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().

4.设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()

更多“设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则 ”相关问题

  • 第1题：

    设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,


    答案：
    解析：
    【解】因为X，Y相互独立且都服从正态分布，所以X，Y的线性组合仍服从正态分布，即2=2X-Y+3服从正态分布，由E(Z)=2E(X)-E(Y)+3=5，D(Z)=4D(X)+D(Y)=9，则Z的密度函数为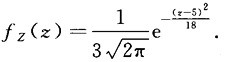

  • 第2题：

    设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.


    答案：
    解析：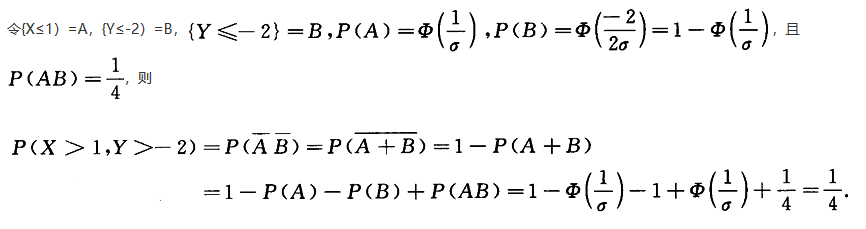

  • 第3题：

    设常数a∈［0,1］,随机变量X～U［0,1］,y=｜X-a｜,则E(XY)=_______.


    答案：
    解析：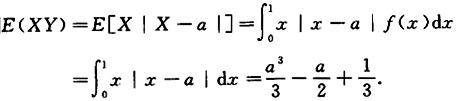

  • 第4题：

    设二维随机变量(X，Y)服从正态分布N(μ，μ；σ^2，σ^2；0)，则E(XY^2)=________.


    答案：
    解析：

  • 第5题：

    设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=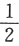.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

    A.A0
    B.1
    C.2
    D.3

    答案：D
    解析：

  • 第6题：

    设X，Y是相互独立的随机变量，X~N（2，σ2），Y~N（-3，σ2），且P{|2X+Y-1|≤8.7654}=0.95，则σ=（）。


    正确答案:2

  • 第7题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第8题：

    若随机变量X～N（3，9），Y～N（－1，5），且X与Y相互独立。设Z＝X－2Y＋2，则Z～（）。


    正确答案:N（7，29）

  • 第9题：

    设X~N（0，1），Y=2X+1，则P{Y-1∣<2}=（）


    正确答案:2Φ（1）-1或0.7

  • 第10题：

    设随机变量X~N（-3，1），Y~N（2，1），且X，Y相互独立，记Z=X-2Y+7，则Z~（）。


    正确答案:N（0，5）

  • 第11题：

    设随机变量X～N（1，4），且P{Xa}=P{Xa}，则a＝（）。


    正确答案:1

  • 第12题：

    单选题
    设随机变量X～N（0，1），Y～N（1，4），且相关系数ρXY＝1，则（　　）。
    A

    P{Y＝－2X－1}＝1

    B

    P{Y＝2X－1}＝1

    C

    P{Y＝－2X＋1}＝1

    D

    P{Y＝2X＋1}＝1


    正确答案： A
    解析：
    令Y＝aX＋b，因为X～N（0，1），Y～N（1，4），则E（Y）＝aE（X）＋b＝1，得b＝1，D（Y）＝a2D（X）＝4，则a＝±2。
    又ρXY＝1，则a＞0，故a＝2。故应选D。

  • 第13题：

    设随机变量X～N(0,1),且y=9X^2,则y的密度函数为_______.


    答案：
    解析：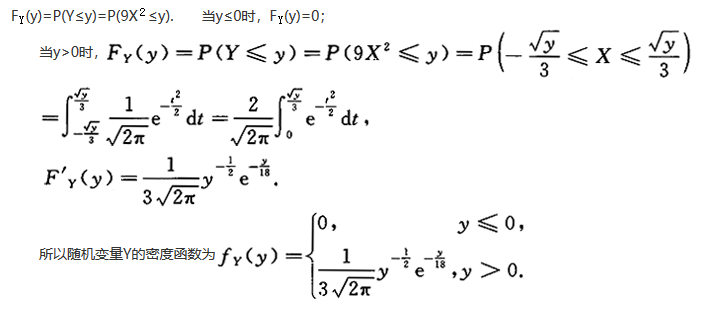

  • 第14题：

    设X,Y相互独立,且X～B,Y～N(0,1),令U=max{X,Y},求P{1

    答案：
    解析：
    【解】P(U≤u)=P(max{X，Y}≤u)=P(X≤u，Y≤u)=P(X≤u)P(Y≤u)，
    P(U≤1.96)=P(X≤1.96)P(Y≤1.96)=［P(X=0)+P(X=1)］P(Y≤1.96)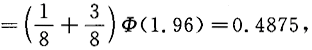

    P(U≤1)=P(X≤1)P(Y≤1)=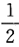×Ф(1)=0.4205，
    则P(1小于U≤1.96)=P(U≤1.96)-P(U≤1)=0.067.

  • 第15题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第16题：

    设二维随机变量(X，Y)服从正态分布N(1，0;1，1;0)，则P{XY-Y<0}=_________.


    答案：
    解析：
    (X，Y)～N(1，0;1，1;0)，所以X与Y相互独立，且X～N(1，1)，Y～N(0，1)也就有(X-1)～N(0，1)与Y相互独立，再根据对称性：P{X-1<0}=P{X-1>0}=P(Y<0)=P{Y>0}=.不难求出P{XY-Y<0}的值.

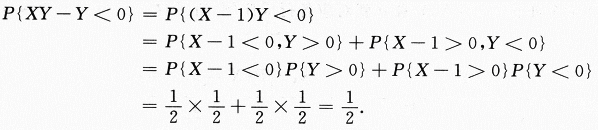
  • 第17题：

    设随机变量X和Y都服从N(0,1)分布，则下列叙述中正确的是（ ）。


    答案：C
    解析：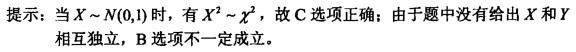

  • 第18题：

    若随机变量X～N（1，4），Y～N（2，9），且X与Y相互独立。设Z＝X－Y＋3，则Z～（）。


    正确答案:N（2，13）

  • 第19题：

    设随机变量X~N（0，1），Y=aX+b（a＞0），则（）

    • A、Y~N（0，1）
    • B、Y~N（b，a）
    • C、Y~N（b，a2）
    • D、Y~N（a+b，a2）

    正确答案:C

  • 第20题：

    设随机变量X与Y相互独立，且X~N（2，22），Y~N（-1，1），则P{|2X+3Y-1|≤9.8}=（）。


    正确答案:0.95

  • 第21题：

    设随机变量X和Y相互独立，且X~N（0，1），Y~N（1，1），则（）

    • A、P{X+Y≤0}=0.5
    • B、P{X+Y≤1}=0.5
    • C、P{X-Y≤0}=0.5
    • D、P{X-Y≤1}=0.5

    正确答案:B

  • 第22题：

    设随机变量X服从N（-1，4），则P｛X+1＜0｝=（）


    正确答案:0.5

  • 第23题：

    设随机变量X～N（1，4），则D（X）=（）


    正确答案:4

  • 第24题：

    单选题
    设随机变量X～N（0，1），Y～N（0，4），且相关系数ρXY=1，则（　　）.
    A

    P{Y=-2X-1}=1

    B

    P{Y=2X-1}=1

    C

    P{Y=-2X+1}=1

    D

    P{Y=2X+1}=1


    正确答案： B
    解析：
    令Y=aX+b，因为X～N（0，1），Y～N（1，4），则EY=aEX+b=1，得b=1，
    D（Y）=a2D2（X）=4，则a=±2.
    又ρXY=1，则a＞0，故a=2.
    故应选D.

相关内容