设随机变量X的概率密度f(x)满足f(1+x)=f(1-x)，且=A.A0.2 B.0.3 C.0.4 D.0.5

题目

设随机变量X的概率密度f(x)满足f(1+x)=f(1-x)，且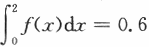

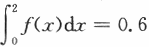A.A0.2
B.0.3
C.0.4
D.0.5

相似考题

1.如果f(x)对任何x都满足f(1＋x)=2f(x),且f(0)存在,f’(0)=2,则f’(1)=()。A．4B．-4C．8D．-8

2.设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().A.F(z)=F（-x） B.F(x)=F（-x） C.F(X)=F（-x） D.f(x)=f（-x）

3.设f′(lnx)=1+x，则f(x)=( )。A. B. C. D.

4.二维连续性随机变量(X,Y)联合概率密度f(x,y)满足f(x,y)0。()

参考答案和解析

答案：A

解析：

更多“设随机变量X的概率密度f(x)满足f(1+x)=f(1-x)，且= ”相关问题

第1题：

设随机变量X的密度函数为f(x)，且f(-x)=f(x)，F(x)是X的分布函数，则对任意实数a有( )。

A.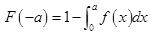
B.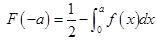
C.F(-a)=F(a)
D.F(-a)=2F(a)-1

答案：B
解析：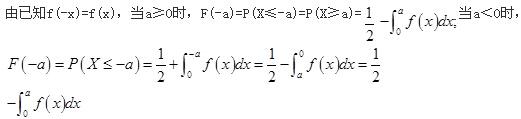
第2题：

设f'（lnx）=1+x，则f（x）等于：

答案：C
解析：
提示：设lnx=t，得f'（t）=1+et形式，写成f'（x）=1+ex，积分。
第3题：

若∫f（x）dx＝F（x）＋C，则∫xf（1－x^2）dx＝（　　）。

A． F（1－x^2）＋C
B．－（1/2）F（1－x^2）＋C
C．（1/2）F（1－x^2）＋C
D．－（1/2）F（x）＋C

答案：B
解析：
∫xf（1－x^2）dx＝（－1/2）∫f（1－x^2）d（1－x^2）＝（－1/2）F（1－x^2）＋C
这里C均表示常数。
第4题：

设随机变量X与Y独立，其中X的概率分布为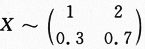而Y的概率密度为f(y)，求随机变量U=X+Y的概率密度g(u).

答案：
解析：
【简解】本题是2003年数三的考题，考查一个离散型和一个连续型两个随机变量的函数的分布，随机变量的独立性等，
先求分布函数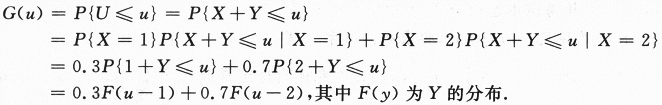

由此得g(u)=0.3f(u-1)+0.7f(u-2).
第5题：

设F1(x)与F2(x)为两个分布函数，其相应的概率密度f1(x)与f2(x)是连续函数，则必为概率密度的是

A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)

答案：D
解析：
第6题：

设随机变量(X，Y)服从二维正态分布，其概率密度为f(x,y)=1/2π

答案：A
解析：
提示 (X，Y)~N(0，0，1，1，0)，X~N(0，1)，Y~N(0，1)，E(X2+Y2) =E(X2)+E(Y2)，E(X2)=D(X) + (E(X) )2
第7题：

设4／（1-x²）·f（x）=d／dx［f（x）］²，且f（0）=0，则f（x）等于：（）
- A、（1+x）／（1-x）+c
- B、（1-x）／（1+x）+c
- C、1n｜（1+x）／（1-x）｜+c
- D、1n｜（1-x）／（1+x）｜+c
正确答案:C
第8题：

设随机变量X的概率密度和分布函数分别是f（x）和F（x），且f（x）=f（-x），则对任意实数a，有F（-a）=（）
- A、1/2-F（a）
- B、1/2+F（a）
- C、2F（a）-1
- D、1-F（a）
正确答案:D
第9题：

设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）

正确答案:0.25
第10题：

设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z=max{X，Y}的分布函数为（）
- A、F²（x）
- B、F（x）F（y）
- C、1-[1-F（x）]²
- D、[1-F（x）][1-F（y）]
正确答案:A
第11题：

单选题
设f（x）＝sinx，f[φ（x）]＝1－x2，则φ（x）＝（　　）。
A
arcsin（1－x）
B
arcsin（1＋x）
C
arcsin（1－x²）
D
arcsin（1＋x²）

正确答案： C
解析：
因sin（arcsinx）＝x，又知f（x）＝sinx，f[φ（x）]＝1－x²，故φ（x）＝arcsin（1－x²）。
第12题：

单选题
设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？
A
f″（x）+f′（x）=0
B
f″（x）-f′（x）=0
C
f″（x）+f（x）=0
D
f″（x）-f（x）=0

正确答案： C
解析：对已知式子两边求导。已知f′（x）=f（1-x），求导f″（x）=-f′（1-x），f（x）+f′（1-x）=0，将1-x代入式子f′（x）=f（1-x），得f′／（1-x）=f[1-（1-x）]=f（x），即f″（x）+f（x）=0
第13题：

设随机变量X的密度函数为f(x),且f(x)为偶函数,X的分布函数为F(x),则对任意实数a,有().

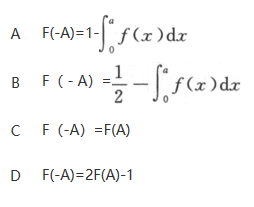答案：B
解析：
第14题：

设随机变量X的分布函数为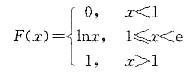则X的概率密度函数f(x)为( )。

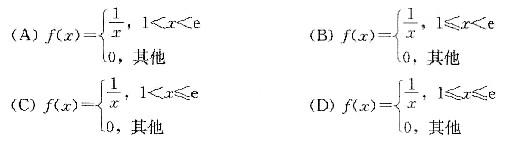答案：B
解析：
由分布函数与概率密度函数关系f(x)=F'(x)，当1≤x＜e时，f(x)=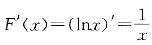，X的概率密度综合表示为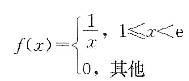
第15题：

设随机变量(X,Y)的联合密度函数为f(x,y)=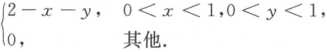(1)求P(X>2Y)；(2)设Z=X+Y,求Z的概率密度函数.

答案：
解析：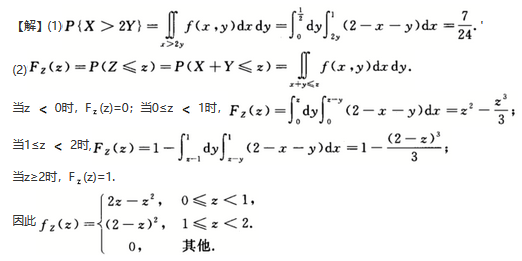
第16题：

设随机变量X，Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为

A.AF^2(x)
B.F(x)F(y)
C.1-［1-F(x)］^2
D.［1-F(x)］［1-F(y)］

答案：A
解析：
随机变量Z=max(X，Y)的分布函数Fz(x)应为Fz(x)=P{Z≤x}，由此定义不难推出Fz(x).【求解】故答案应选(A).
【评注】不难验证(B)F(x)F(y)恰是二维随机变量(X，Y)的分布函数.(C)1-［1-F(x)］^2则是随机变量min(X，Y)的分布函数.(D)［1-F(x)］［1-F(y)］本身不是分布函数，因它不满足分布函数的充要条件.
第17题：

设随机变量x的概率密度为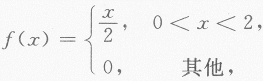F(x)为X的分布函数，EX为X的数学期望，则P{F(X)>EX-1}=________.

答案：
解析：
第18题：

设随机变量x的密度函数为f(x)，且f(-x)=f（x)，F(x)是X的分布函数，则对任意实数 a，有( )。

答案：B
解析：
第19题：

设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？
- A、f″（x）+f′（x）=0
- B、f″（x）-f′（x）=0
- C、f″（x）+f（x）=0
- D、f″（x）-f（x）=0
正确答案:C
第20题：

设F₁（x）与F₂（x）为两个分布函数，其相应的概率密度f₁（x）与f₂（x）是连续函数，则必为概率密度的是（）
- A、f₁（x）f₂（x）
- B、2f₂（x）F₁（x）
- C、f₁（x）F₂（x）
- D、f₁（x）F₂（x）+f₂（x）F₁（x）
正确答案:D
第21题：

设X₁，X₂是任意两个相互独立的连续型随机变量，它们的概率密度分别为f₁（x）与f₂（x），分布函数分别为F₁（x）与F₂（x），则（）
- A、f₁（x）+f₂（x）必为某一随机变量的概率密度
- B、f₁（x）f₂（x）必为某一随机变量的概率密度
- C、F₁（x）+F₂（x）必为某一随机变量的分布函数
- D、F₁（x）F₂（x）必为某一随机变量的分布函数
正确答案:D
第22题：

问答题
随机变量(X，Y)在矩形区域D={(x，y)|a 　　求：(1)联合概率密度f(x，y). 　　(2)边缘概率密度f X(i)，f Y(y). 　　 (3)X与Y是否独立?

正确答案：
解析：
第23题：

单选题
设4／（1-x2）·f（x）=d／dx［f（x）］2，且f（0）=0，则f（x）等于：（）
A
（1+x）／（1-x）+c
B
（1-x）／（1+x）+c
C
1n｜（1+x）／（1-x）｜+c
D
1n｜（1-x）／（1+x）｜+c

正确答案： A
解析：计算等号右边式子，得到f′（x）表达式。计算不定积分。

设随机变量X的概率密度f(x)满足f(1+x)=f(1-x)，且=A.A0.2 B.0.3 C.0.4 D.0.5

题目

相似考题

参考答案和解析

更多“设随机变量X的概率密度f(x)满足f(1+x)=f(1-x)，且= ”相关问题

相关内容