当a,b取何值时,方程组无解、有唯一解、有无数个解?在有无数个解时求出其通解.
题目
当a,b取何值时,方程组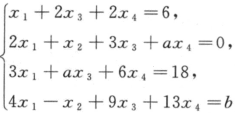 无解、有唯一解、有无数个解?在有无数个解时求出其通解.
无解、有唯一解、有无数个解?在有无数个解时求出其通解.
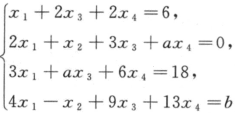 无解、有唯一解、有无数个解?在有无数个解时求出其通解.
无解、有唯一解、有无数个解?在有无数个解时求出其通解.相似考题
更多“当a,b取何值时,方程组无解、有唯一解、有无数个解?在有无数个解时求出其通解.”相关问题
-
第1题:
设齐次线性方程组 其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解.答案:解析:
其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解.答案:解析:
-
第2题:
k取何值时,方程组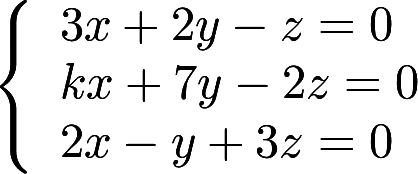 仅有零解?答案:解析:
仅有零解?答案:解析: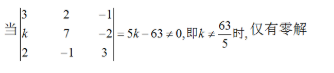
-
第3题:
设齐次线性方程组
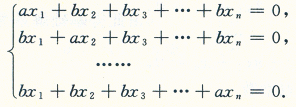
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.答案:解析:
-
第4题:
齐次方程组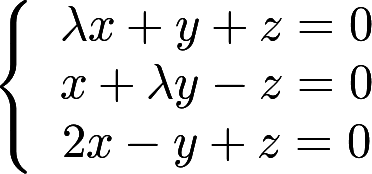 .当
.当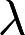 取何值时,才可能有非零解?并求解.答案:解析:
取何值时,才可能有非零解?并求解.答案:解析:
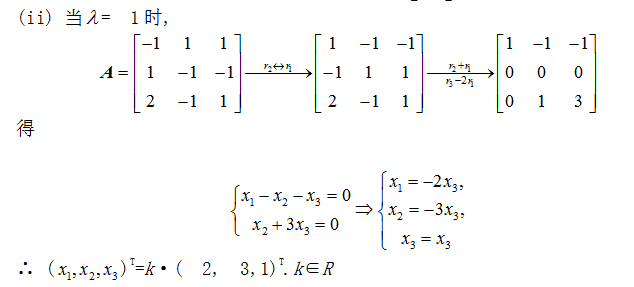
-
第5题:
问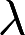 取何值时 非齐次线性方程组
取何值时 非齐次线性方程组 , (1)有唯一解 (2)无解 (3)有无穷多个解,并在无穷多个解时,求方程组的通解答案:解析:
, (1)有唯一解 (2)无解 (3)有无穷多个解,并在无穷多个解时,求方程组的通解答案:解析:
-
第6题:
设有齐次线性方程组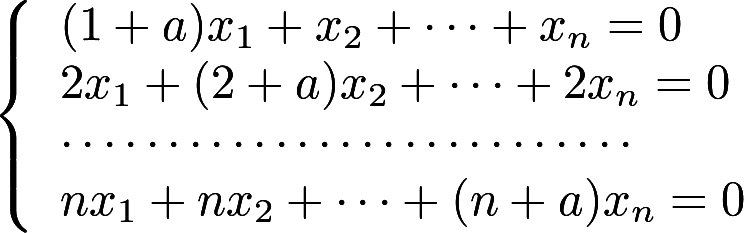
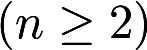 .试问
.试问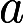 取何值时,该方程组有非零解,并求出其通解答案:解析:
取何值时,该方程组有非零解,并求出其通解答案:解析:

-
第7题:
当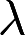 取何值时,方程组
取何值时,方程组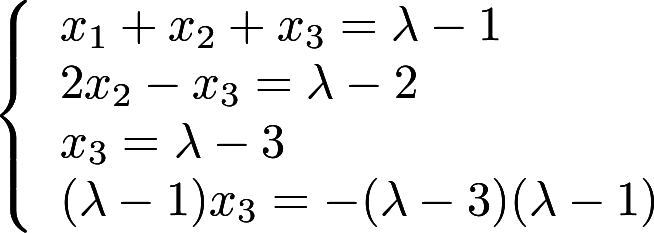 有唯一解,并求解。答案:解析:
有唯一解,并求解。答案:解析:
-
第8题:
问 取何值时,齐次方程组
取何值时,齐次方程组 有非零解?答案:解析:
有非零解?答案:解析:
-
第9题:
设n元线性方程组Ax=b,其中
.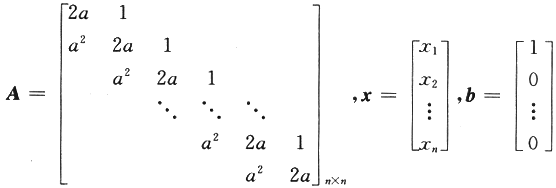
(Ⅰ)证明行列式|A|=(n+1)a^n;
(Ⅱ)当a为何值时,该方程组有唯一解,并求x1;
(Ⅲ)当a为何值时,该方程组有无穷多解,并求通解.答案:解析:
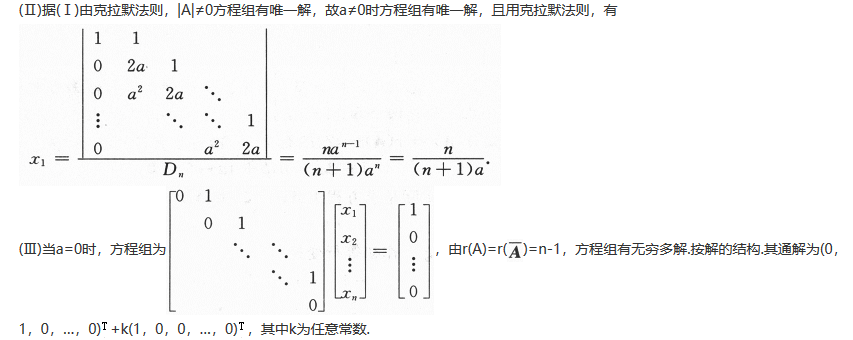


-
第10题:
非齐次线性方程组AX=b中未知数个数为n,方程个数为m,系数矩阵A的秩为r,则( ).A.r=m时,方程组AX=b有解
B.r=n时,方程组AX=b有唯一解
C.m=m时,方程组AX=b有唯一解
D.r<n时,方程组AX=b有无穷多解答案:A解析:
-
第11题:
两阶段法的辅助问题的最优值g>0时,原问题()。
- A、无解
- B、有唯一解
- C、无界
- D、有无穷多个解
正确答案:A -
第12题:
单选题非齐次线性方程组AX(→)=b(→)中未知数个数为n,方程个数为m,系数矩阵A的秩为r,则( )。Ar=m时,方程组AX=b有解
Br=n时,方程组AX=b有唯一解
Cm=n时,方程组AX=b有唯一解
Dr<n时,方程组AX=b有无穷多解
正确答案: A解析:
A项,由于r=m,则方程组AX=b的增广矩阵化为阶梯形矩阵时,阶梯形矩阵不为0的行数为m,r(A)=r(A)=m,所以AX=b有解;
B项,当r=n时,可知n≤m,当n<m时,则方程组AX=b不一定只有唯一解;
C项,当m=n时,r(A)不一定等于r,方程组不一定有解;
D项,当r<n时,不能保证r(A)=r(A)=r,方程组AX=b不一定有解。 -
第13题:
参数a取何值时,线性方程组 有无数个解?并求其通解.答案:解析:
有无数个解?并求其通解.答案:解析:
-
第14题:
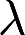 取何值时,非齐次线性方程组
取何值时,非齐次线性方程组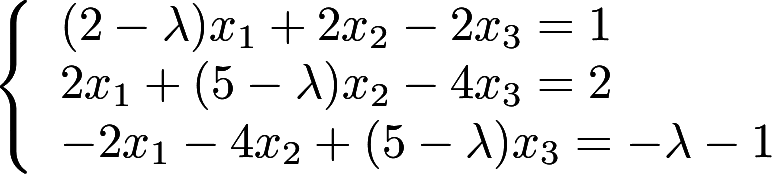 (1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时,求方程组的通解。答案:解析:
(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时,求方程组的通解。答案:解析:

-
第15题:
常数k取何值时, 方程组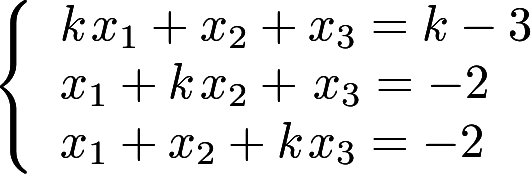 无解, 有惟一解或有无穷多解? 当方程组有无穷多解时求其通解答案:解析:
无解, 有惟一解或有无穷多解? 当方程组有无穷多解时求其通解答案:解析:
-
第16题:
 取何值时,方程组
取何值时,方程组 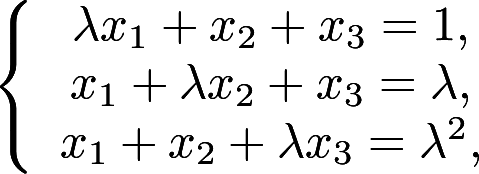 (1)有惟一解;(2)无解;(3)有无穷多解,并求解答案:解析:
(1)有惟一解;(2)无解;(3)有无穷多解,并求解答案:解析:

-
第17题:
已知下列非齐次线性方程组(Ⅰ),(Ⅱ)
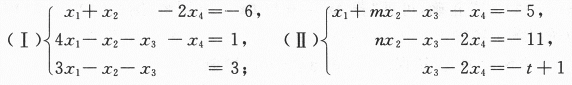
(1)求解方程组(Ⅰ),用其导出组的基础解系表示通解.
(2)当方程组中的参数m,n,t为何值时,方程组(Ⅰ)与(Ⅱ)同解.答案:解析:
-
第18题:
当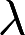 取何值时,下列线性方程组有解?有解时,求出其全部解:
取何值时,下列线性方程组有解?有解时,求出其全部解: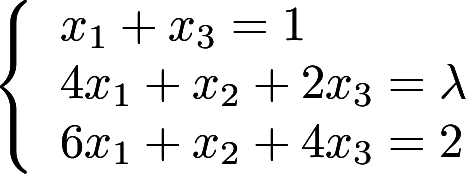 答案:解析:
答案:解析:
-
第19题:
确定a的值,使方程组 有无穷多个解,求出它的通解。答案:解析:
有无穷多个解,求出它的通解。答案:解析:
-
第20题:
设矩阵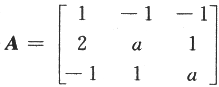
 ,.
,.
当a为何值时,方程AX=B无解、有唯一解、有无穷多解?在有解时,求解此方程.答案:解析:
-
第21题:
设线性方程组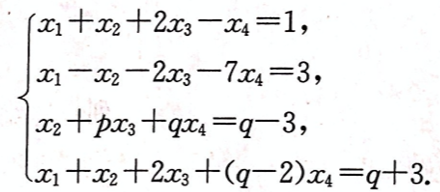 问方程组何时无解,有唯一解,有无穷多解,有无穷多解时,求出其全部解。答案:解析:将方程组的增广矩阵作初等行变换,有
问方程组何时无解,有唯一解,有无穷多解,有无穷多解时,求出其全部解。答案:解析:将方程组的增广矩阵作初等行变换,有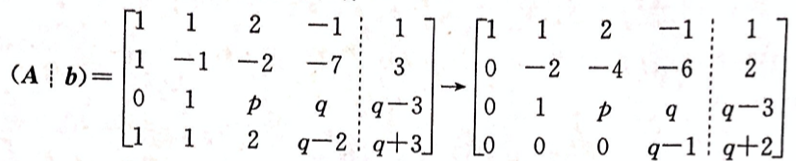
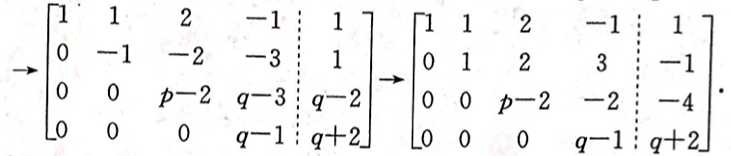
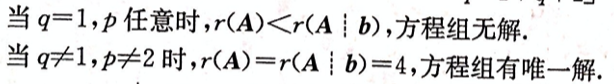
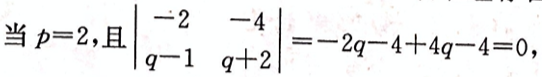

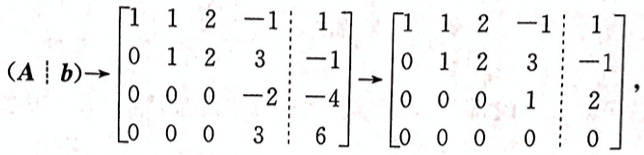

-
第22题:
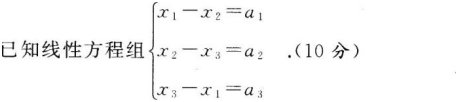
(1)讨论常数a1,a2,a3满足什么条件时,方程组有解.
(2)当方程组有无穷多解时,求出其通解(要求用它的一个特解和导出组的基础解系表示).答案:解析:解:(1)将其增广矩阵化为简化行阶梯形矩阵T
-
第23题:
单选题若“未知数个数”大于“方程个数”,则可确定:()。A方程无解
B方程有非零解
C方程有唯一解
D无法确定
正确答案: D解析: 暂无解析
