设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立

题目
设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立

相似考题

1.设A,B均为n阶方阵,则()A、若|A+AB|=0，则|A|=0或|E+B|=0B、(A+B)^2=A^2+2AB+B^2C、当AB=O时，有A=O或B=OD、(AB)^-1=B^-1A^-1

2.设矩阵A,B,C,X为同阶方阵,且A,B可逆,AXB=C,则矩阵X=()A、A^-1CB^-1B、CA^-1B^-1C、B^-1A^-1CD、CB^-1A^-1

3.设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=1。()此题为判断题(对，错)。

4.设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=()A、-1B、-2C、1D、2

更多“设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立”相关问题

  • 第1题：

    设A、B均为三阶方阵，且行列式|A|＝1，|B|＝－2，A^T为A的转置矩阵，则行列式|－2A^TB^－1|＝（　　）。

    A． －1
    B． 1
    C． －4
    D． 4

    答案：D
    解析：
    因为A、B均为三阶方阵，计算得
    |－2A^TB^－1|＝（－2）^3×|A^T|×|B^－1|＝（－2）^3×1×（1/－2）＝4

  • 第2题：

    设A为n阶可逆方阵，则( )不成立。

    A.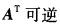
    B.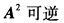
    C.-2A可逆
    D.A+E可逆

    答案：D
    解析：

  • 第3题：

    设A与B都是n阶方阵,且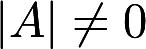,证明AB与BA相似.


    答案：
    解析：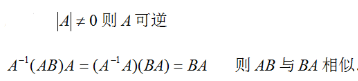

  • 第4题：

    设向量组α1,…,αn为两两正交的非零向量组,证明：α1,…,αn线性无关,并举例说明逆命题不成立.


    答案：
    解析：

  • 第5题：

    设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B， (1)证明B可逆； (2)求.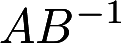


    答案：
    解析：

  • 第6题：

    设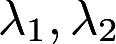为n阶方阵A的两个互不相等的特征值,与之对应的特征向量分别为X1,X2,证明X1,X2不是矩阵A的特征向量。


    答案：
    解析：

  • 第7题：

    设3阶矩阵A=［α1，α2，α3］有3个不同的特征值，且a3=a1+2a2.
    　　(Ⅰ)证明r(A)=2；
    　　(Ⅱ)若β=α1，α2，α3，求方程组Ax=β的通解.


    答案：
    解析：

  • 第8题：

    问答题
    已知A＝（aij），B＝（bij）为两个n阶方阵。　　X为n阶方阵。证明：AX＝B有解的充要条件是n＋1个矩阵A，A1，A2，…，An的秩相等。

    正确答案：
    (1)必要性
    设AX=B有解,令X(→)1,X(→)2,…,X(→)n是X的列向量,B(→)1,B(→)2,…,B(→)n是B的列向量。由AX=B有解知方程组AX(→)k=B(→)k(k=1,2,…,n)有解,于是有r(A)=r(A┆B(→)k)=r(Ak)(k=1,2,…,n),即A,A1,A2,…,An的秩相等。
    (2)充分性
    若A,A1,A2,…,An的秩都相等,则方程组AX(→)k=B(→)k有解。记其解为C(→)i(i=1,2,…,n),则AC=B(其中C是以Ci为列向量的矩阵),即C为AX=B的解,故AX=B有解。
    解析： 暂无解析

  • 第9题：

    填空题
    设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝____。

    正确答案： -(A+E)/2
    解析：
    由题设A2＝A有，A2－A－2E＝（A－2E）（A＋E）＝－2E，即（A－2E）[－（A＋E）/2]＝E，所以有（A－2E）－1＝－（A＋E）/2。

  • 第10题：

    单选题
    设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（　　）。
    A

    ｜A｜2

    B

    ｜A｜n

    C

    ｜A｜2n

    D

    ｜A｜2n－1


    正确答案： D
    解析：
    ||A|A*|＝|A|n·|A*|＝|A|n·|A|n－1＝|A|2n－1。

  • 第11题：

    单选题
    设A、B均为三阶方阵，且行列式|A|＝1，|B|＝－2，AT为A的转置矩阵，则行列式|－2ATB－1|＝（　　）。[2018年真题]
    A

    －1

    B

    1

    C

    －4

    D

    4


    正确答案： B
    解析：
    因为A、B均为三阶方阵，计算得|－2ATB－1|＝（－2）3×|AT|×|B－1|＝（－2）3×1×（－1/2）＝4。

  • 第12题：

    问答题
    设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.

    正确答案：
    证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
    所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.
    解析： 暂无解析

  • 第13题：

    若A,B均为n阶方阵,则当|A|>|B|时，A,B一定不相似


    答案：对
    解析：
    正确，因为相似矩阵必须有相同特征值和行列式

  • 第14题：

    如右图，在梯形ABCD中，点E、F分别是腰AB、CD上的点．
    (1)证明：如果E、F为中点时，有 EF=1/2(AD+BC)；
    (2)请写出(1)中命题的逆命题，并判断该逆命题是否成立，若成立，请给予证明；若不成立，请说明理由．



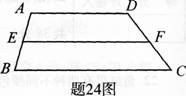    答案：
    解析：
    (1)证明：连接AC，设AC中点为日，连接EH、FH



    逆命题不成立.
    理由如下：连接AC，连接BD，延长AD至M使DM=AD，延长BC至N，使CN=AD，连接MN、DN.由DM平行且等于CN可知，DN平行且等于AC由ADBN可知，BD+DM>BN，即BD+AC>BC+AD



    又AD＜EF可知AD＜EF＜BD过点D作直线交AB于Q，则AD＜DQ＜BD，其中必有DQ=EF同理，若AC>EF，Q为DC上-点，则必有AQ=EF且A、D均不是AB、CD的中点故命题错误.

  • 第15题：

    设A,B为n阶矩阵.
    　　(1)是否有AB～BA；(2)若A有特征值1,2,…,n,证明：AB～BA.


    答案：
    解析：

  • 第16题：

    设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B.
    　　(1)证明B可逆；
    　　(2)求AB^-1.


    答案：
    解析：

  • 第17题：

    设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.


    答案：
    解析：

  • 第18题：

    设二维非零向量α不是二阶方阵A的特征向量.
    　　(1)证明α,Aα线性无关；
    　　(2)若Aα^2+Aα-6α=0,求A的特征值,讨论A可否对角化；


    答案：
    解析：

  • 第19题：

    设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．

    • A、3
    • B、2
    • C、1
    • D、0

    正确答案:D

  • 第20题：

    单选题
    设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： B
    解析： 暂无解析

  • 第21题：

    单选题
    设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： A
    解析：
    取基本单位向量组为ε(→)1，ε(→)2，…，ε(→)n。
    当m＝n时，由对任意B都有AB＝0，则对B＝（ε(→)1，ε(→)2，…，ε(→)n）＝En也成立，即AE＝0，故A＝0。
    当m＞n时，取B＝（ε(→)1，ε(→)2，…，ε(→)n，B(→)1）＝（En，B(→)1），则由AB＝A（En，B(→)1）＝0，知AEn＝0，故A＝0。

  • 第22题：

    单选题
    设A为4阶方阵，且r（A）＝3，A*为A的伴随矩阵，则r（A*）＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： B
    解析：
    由A是4阶方阵且r（A）＝3，知|A|＝0，又AA*＝|A|E＝0为A的齐次方程组，则A*的列向量是齐次方程组Ax(→)＝0(→)的解，故r（A）＋r（A*）≤4，则r（A*）≤1。由r（A）＝3知，A至少有一个代数余子式不为0，故A*≠0，所以r（A*）＝1。

  • 第23题：

    问答题
    设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。

    正确答案：
    由对任意n维向量x(→)都有Ax(→)=0,知对基本单位向量组ε(→)1,ε(→)2,…,ε(→)n,Aε(→)i=0(i=1,2,…,n)成立。
    所以有A(ε(→)1,ε(→)2,…,ε(→)n)=0,即AE=0,故A=0。
    解析： 暂无解析

相关内容