设α1=(1，2，-1，0)^T，α2=(1，1，0，2)^T，α3=(2，1，1，α)^T.若由α1，α2，α3生成的向量空间的维数为2，则α=________.
题目
设α1=(1，2，-1，0)^T，α2=(1，1，0，2)^T，α3=(2，1，1，α)^T.若由α1，α2，α3生成的向量空间的维数为2，则α=________.
相似考题
参考答案和解析
答案：1、6.
解析：
本题考查向量空间及其维数的概念，因为α1，α2，α3所生成的向量空间是2维，亦即向量组的秩r(α1，α2，α3)=2
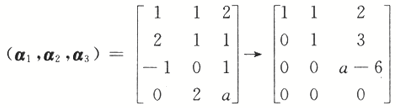
由秩为2，知α=6.
由秩为2，知α=6.
更多“设α1=(1，2，-1，0)^T，α2=(1，1，0，2)^T，α3=(2，1，1，α)^T.若由α1，α2，α3生成的向量空间的维数为2，则α=________.”相关问题
-
第1题：
设α,β为四维非零列向量,且α⊥β,令A=αβ^T,则A的线性无关特征向量个数为().A.1
B.2
C.3
D.4答案：C解析：
-
第2题：
设向量组A：a1=(1，0，5，2)，a2=(-2，1，-4，1)，a3=(-1，1，t，3)，a4=(-2，1，-4，1)线性相关，则t必定等于( ).A.1
B.2
C.3
D.任意数答案：D解析： -
第3题：
在线性空间R3中，已知向量a1=(1，2，1)，a2=(2，1，4)，a3=(0，-3，2)，
记V1={λa1+μa2|λ，μ∈R}，V2={ka3|k∈R}。
令V3={t1η1+t2η2|t1，t2∈R，η1∈V1，η2∈V2}。
(1)求子空间V3的维数；
(2)求子空间V3的一组标准正交基。答案：解析：
-
第4题：
已知λ= 2是三阶矩A的一个特征值，α1、α2是A的属于λ= 2的特征向量。 若α1=(1,2,0)T，α2=(1,0,1)T，向量β= (-1,2,-2)T,则Aβ等于（ ）。
A. (2,2,1)T B. (-1,2,-2)T C. (-2,4,-4)T D. (-2,-4,4)答案：C解析：
-
第5题：
设向量组A：α1=（t，1，1），α2=（1，t，1），α3=（1，1，t）的秩为2，则t等于（）．
- A、1
- B、-2
- C、1或-2
- D、任意数
正确答案:B -
第6题：
设向量组A：α1=（1，0，5，2），α2=（-2，1，-4，1），α3=（-1，1，t，3），α4=（-2，1，-4，1）线性相关，则t必定等于（）．
- A、1
- B、2
- C、3
- D、任意数
正确答案:D -
第7题：
填空题设α=（1，0，-1，2），β=（0，1，0，2），则r（αTβ）=____.正确答案： 1解析：
知，r（αTβ）≤min[r（αT），r（β）]=1又αβ均不是零向量，故r（αTβ）＞0，知r（αTβ）=1． -
第8题：
单选题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（ ）。Ak（0，1，1，1）T＋（1，1，0，2）T/2
Bk（0，1，－1，－1）T＋（1，1，0，2）T/2
Ck（0，1，1，－1）T＋（1，1，0，2）T/2
Dk（0，1，－1，1）T＋（1，1，0，2）T/2
正确答案： C解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。 -
第9题：
问答题设向量组（Ⅰ）α1，α2，…，αs．（Ⅱ）β1，β2，…，βt．（Ⅲ）α1，α2，…，αs，β1，β2，…，βt．的秩依次为r1，r2，r3.证明:max（r1，r2）≤r3≤r1+r2.正确答案：
当r1,r2中有一个为0的,等式显然成立.
当r1≠0,r2≠0,设向量组①:α1,α2,…,αr1;②:β1,β2,…,βr2;③:δ1,δ2,…,δr3分别是向量组(Ⅰ)、(Ⅱ)和(Ⅲ)的极大线性无关组.
显然③可由①和②线性表示,又③线性无关,故r3≤r1+r2.由于①、②可由③线性表示,所以r1≤r3,r2≤r3,即max(r1,r2)≤r3.所以max(r1,r2)≤r3≤r1+r2.解析： 暂无解析 -
第10题：
填空题设α(→)＝（1，0，－1，2）T，β(→)＝（0，1，0，2），矩阵A＝α(→)·β(→)，则秩r（A）＝____。正确答案： 1解析：
秩r（A）＝r（α·β）≤r（α）＝1，又α·β≠0，可见r（A）≥1。故r（A）＝1。 -
第11题：
单选题设α(→)1，α(→)2，…，α(→)s和β(→)1，β(→)2，…，β(→)t为两个n维向量组，且秩（α(→)1，α(→)2，…，α(→)s）＝秩（β(→)1，β(→)2，…，β(→)t）＝r，则（ ）。A此两个向量组等价
B秩（α1，α2，…，αs，β1，β2，…，βt）＝r
C当α1，α2，…，αs可以由β1，β2，…，βt线性表示时，此二向量组等价
Ds＝t时，二向量组等价
正确答案： C解析：
两向量组等价的充要条件是所含向量的个数相等，且能相互线性表示。 -
第12题：
单选题设α(→)＝（1，0，－1，2）T，β(→)＝（0，1，0，2），矩阵A＝α(→)·β(→)，则秩r（A）＝（ ）。A2
B1
C3
D4
正确答案： A解析：
秩r（A）＝r（α·β）≤r（α）＝1，又α·β≠0，可见r（A）≥1。故r（A）＝1。 -
第13题：
设向量组A：a1=(1，-1，0)，a2=(2，1，t)，a3=(0，1，1)线性相关，则t等于( ).A.1
B.2
C.3
D.0答案：C解析：
-
第14题：
设矩阵
，α1，α2，α3为线性无关的3维列向量组，则向量组Aα1，Aα2，Aα3的秩为_________.答案：1、2.解析：因(Aα1，Aα2，Aα3)=A(α1，α2，α3)，又α，α，α是三维线性无关列向量，所以(α1，α2，α3)为三阶可逆矩阵故r(Aα1，Aα2，Aα3)=r(A)=2. -
第15题：
设向量组α1=(1，0，1)T，α2=(0，1，1)T，a3=(1，3，5)T，不能由向量组β1，=(1，1，1)T,f12=(1，2，3)T，3β=(3，4，α)T线性表示。
(1)求a的值；
(2)将β1β2β2由α1α2α3线性表示。答案：解析：(1)由于α1，α2，α3不能由β1β2β3，线性表示，对（β１，β２，β３，α１，α２，α３进行初等变换∶
故β１＝２α１＋４α２－α３，β２＝α１＋２α２，β３＝５α１＋１０α２－２α３ -
第16题：
已知λ=2是三阶矩阵A的一个特征值，α1，α2是A的属于λ=2的特征向量。若α1=（1，2，0）T，α2=（1，0，1）T，向量β=（-1，2，-2）T，则Aβ等于（）。
- A、（2，2，1）T
- B、（-1，2，_2）T
- C、（-2，4，-4）T
- D、（-2，-4，4）
正确答案:C -
第17题：
设向量组A：α1=（1，-1，0），α2=（2，1，t），α3=（0，1，1）线性相关，则t等于（）。
- A、1
- B、2
- C、3
- D、0
正确答案:C -
第18题：
设列向量p=［1，-1，2］T是3阶方阵相应特征值λ的特征向量，则特征值λ等于（）．
- A、3
- B、5
- C、7
- D、不能确定
正确答案:B -
第19题：
填空题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是____。正确答案： k(0,1,-1,-1)T+(1,1,0,2)T/2解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。 -
第20题：
单选题设向量组A：α1=（t，1，1），α2=（1，t，1），α3=（1，1，t）的秩为2，则t等于（）．A1
B-2
C1或-2
D任意数
正确答案： D解析： 暂无解析 -
第21题：
单选题设α(→)＝（1，0，－1，2），β(→)＝（0，1，0，2），则r（α(→)Tβ(→)）＝（ ）。A1
B2
C3
D4
正确答案： A解析：
r（αTβ）≤min[r（αT），r（β）]＝1，又αTβ≠0，故r（αTβ）＞0，知r（αTβ）＝1。 -
第22题：
单选题设n维向量组（Ⅰ）α(→)1，α(→)2，…，α(→)s线性无关，（Ⅱ）β(→)1，β(→)2，…，β(→)t线性无关，且α(→)i不能由（Ⅱ）线性表示（i＝1，2，…，s），且β(→)j不能由（Ⅰ）线性表示（j＝1，2，…，t），则向量组α(→)1，α(→)2，…，α(→)s，β(→)1，β(→)2，…，β(→)t（ ）。A一定线性相关
B一定线性无关
C可能线性相关，也可能线性无关
D既不线性相关，也不线性无关
正确答案： C解析：
设（Ⅰ）：α1＝（1，0，0），α2＝（1，1，0），（Ⅱ）：β1＝（0，0，1），β2＝（0，1，1）。则向量组（Ⅰ）和（Ⅱ）各自线性无关，但α1，α2，β1，β2线性相关；
令（Ⅱ）：β1＝（0，0，1），α1，α2，β1也满足条件，但α1，α2，β1线性无关。 -
第23题：
单选题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（ ）。Ak（0，1，－1，－1）T＋（1，1，0，2）T
Bk（0，1，－1，－1）T＋（1，1，0，2）T/2
Ck（1，1，0，2）T＋（0，1，－1，－1）T
Dk（1，1，0，2）T＋（0，1，－1，－1）T/2
正确答案： D解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。
又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。