设,(t为参数)，则=_________.

第1题：

设f(t)=t+cost+e2t，则=( )。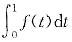

答案：D

解析：

由于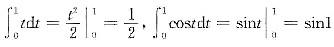

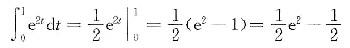
第2题：

理想气体处于平衡状态，设温度为T，分子自由度为i，则每个气体分子具有的( )。

第3题：

设参数方程 ，确定了y是x的函数，f''(t)存在且不为零，则d2y/dx2
的值是：

答案：D

解析：

提示:利用参数方程求导公式求出dy/dx，在求二阶导数时，先对t求导后，再乘t对x的导数。计算如下：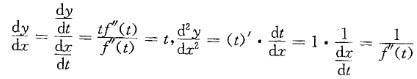

第4题：

设随机变量X服从参数为A的指数分布,则P{X>)=_______.

答案：

解析：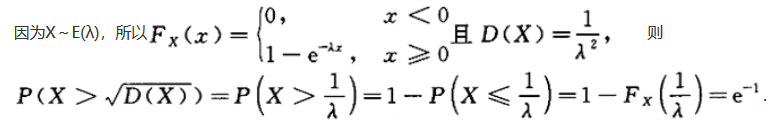

第5题：

设随机变量X服从参数为λ的指数分布，则=_______.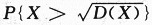

答案：

解析：

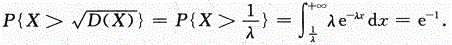答案应填e.

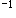
第6题：

第7题：

答案：

解析：

【证明】(Ⅰ)因为α，β为三维列向量，那么αα^T和ββ^T都是三阶矩阵，
且秩r(αα^T)≤1，r(ββ^T)≤1.
那么，r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
(Ⅱ)由于α，β线性相关，不妨设α=kβ，于是
r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
【评注】本题考查矩阵秩的性质公式.
(Ⅰ)中有两个基本知识点：①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
(Ⅱ)中有两个基本知识点：①α，β线性相关的几何意义和②r(kA)=r(A)，k≠0.
注意，如果分块矩阵比较熟悉，本题的(Ⅰ)也可如下处理：
因为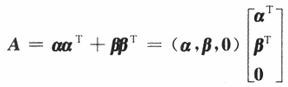

那么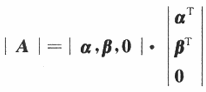
从而r(A)≤2.

第8题：

设随机变量Y服从参数为1的指数分布，a为常数且大于零，则P{Y≤a+1|Y>a}=（）

第9题：

设信号x（t）的自功率谱密度函数为常数，则其自相关函数为（）。

第10题：

在某一平差问题中，观测数为n，必要观测数为t，参数个数u＜t且不独立，则该平差问题可采用附有参数的条件平差的函数模型。

第11题：

第12题：

第13题：

1. 设直线L的方程为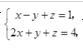

则L的参数方程是（　　）。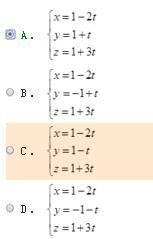

答案：A

解析：

过点M0（x0，y0，z0）的直线，s=（m，n，p）为其一个方向向量，若设参数t如下：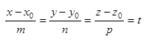

则其参数式方程可写作

直线的方向向量应与所在两个平面的法向量都垂直，即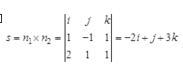

直线过点（1，1，1），从而参数方程为：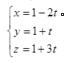

第14题：

设二次型要使f的秩为2，则参数t的值等于（　　）。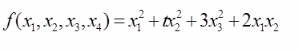

A．3
B．2
C．1
D．0

答案：C

解析：

第15题：

设参数方程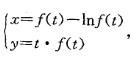确定了y是x的函数，且f(t)存在，f(0) = 2，
f(0) = 2，则当t=0时，dy/dx的值等于：
A. 4/3 B. -4/3 C. -2 D. 2

答案：C

解析：

提示:利用参数方程导数公式计算出dy/dx，代入t=0，得到t=0时的dy/dx值。计算如下：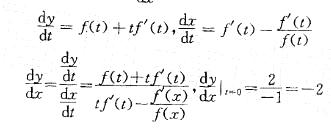

第16题：

答案：1、0

解析：

第17题：

设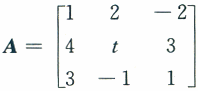，B为三阶非零矩阵，且AB=0，则t=________.

答案：1、-3.

解析：

由AB=0，对B按列分块有AB=A(β1，β2，β3)=(Aβ1，Aβ2，Aβ3)=(0,0,0)，即β1，β2，β3是齐次方程组Ax=0的解，又因B≠0，故Ax=0有非零解，那么若熟悉公式：AB=0，则r(A)+r(B)≤n.可知r(A)<3.亦可求出t=-3.
【评注】对于AB=O要有B的每个列向量都是齐次方程组Ax=0的构思，还要有秩r(A)+r(B)≤n的知识.

第18题：

设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X

答案：A

解析：

X～E(1)，Y～E(4)且相互独立，所以(X，Y)的概率密度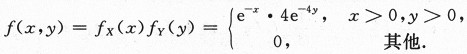　　
　　利用公式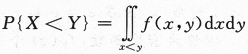可以计算出结果.
　　【求解】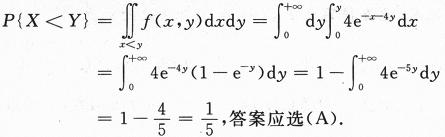

第19题：

设随机变量X服从参数为3的泊松分布，则E（X-3）=（）

第20题：

设随机变量X服从参数为2的泊松分布，且Y=3X-2，则E（Y）=（）。

第21题：

有一单摆，在山脚下测得周期为T₁，移到山顶测得周期为了T₂，设地球半径为R，则山的高度为（）。

第22题：

设某周期信号x（t）之单位为μ，则其均方根谱之单位为μ²，其功率谱之单位为μ。

第23题：