计算斐波那契数列第n项的值。在数学上,斐波那契数列以如下递归方法定义: F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*) 斐波那契数列的前几项是如下的数字: 1、1、2、3、5、8、13、21、34、......
题目
计算斐波那契数列第n项的值。在数学上,斐波那契数列以如下递归方法定义: F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*) 斐波那契数列的前几项是如下的数字: 1、1、2、3、5、8、13、21、34、......
相似考题
参考答案和解析
更多“计算斐波那契数列第n项的值。在数学上,斐波那契数列以如下递归方法定义: F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*) 斐波那契数列的前几项是如下的数字: 1、1、2、3、5、8、13、21、34、......”相关问题
-
第1题:
下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1,即F(1)=1,F(2)=1;而后面各项满足: F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句,使程序的功能完整。
注意:请勿改动main()主方法和其他已有的语句内容,仅在横线处填入适当的语句。
public class Fibonacci{
public static void main(String args[]){
System.out.printtn("Fibonacci is"+" "+"_______________________);
}
static long fib(int n){
if(______________)
return 1;
else
return _________________
}
}
正确答案:fib(10) n==0||n==1 fib(n-1)+fib(n-2);
fib(10) n==0||n==1 fib(n-1)+fib(n-2); 解析:本题主要考查递归算法。解答本题的关键是理解递归算法的思想。在本题中,fib(10)方法是计算含由10项的菲波那契 (Fibonacci)数列,而fib(n-1)+fib(n-2);是用来计算第0项和第1项以外的菲波那契(Fibonacci)数列。 -
第2题:
下列给定程序中,函数fun()的功能是:用递归算法计算斐波拉契级数列中第n项的值。从第一项起,斐波`拉契级数序列为1, 1,2,3,5,8,13,21,……例如,若给n输入7,
该项的斐波拉契级数值为13。
请改正程序中的错误,使它能得出正确的结果。
注意:不要改动main函数,不得增行或删行,也不得更改程序的结构。
试题程序:
include <stdio.h>
long fun(int g)
{
/*************found**************/
switch(g);
{case 0:return 0;
switch(g)
case 1; case 2:return 1;
}
return (fun(g-1)+fun(g-2));
}
main()
{
long fib; int n;
printf("Input n:");scanf("%d",&n);
printf("n-%d\n",n);
fib=fun(n);
printf("fib=%d\D\n",fib);
}
正确答案:(1)错误:switch(g); 正确:去掉分号 (2)错误:case 1;case 2:return 1: 正确:case 1:case 2:return 1;
(1)错误:switch(g); 正确:去掉分号 (2)错误:case 1;case 2:return 1: 正确:case 1:case 2:return 1; 解析:C语言中,Switch语句之后不能有分号,并且Case语句常量后应用的是冒号。 -
第3题:
计算斐波那契数列第n项的函数定义如下:
int fib(int n){
if(n==0) return 1;
else if(n==1)return 2;
else return fib(n-1)+ilb(n-2);
}
若执行函数调用表达式fib(2),函数fib被调用的次数是
A.1
B.2
C.3
D.4
正确答案:C
解析:fib(2)=fib(1)+fib(O)=2+1=3,所以函数被调用3次,分别是fib(2)、fib(1)和fib(O)。 -
第4题:
下列给定程序中函数fun的功能是。用递归算法计算斐波拉契数列中第n项的值。从第l项起,斐波拉契数列为:1、1、2、3、5、8、l3、21、……
例如,若给n输入7,则该项的斐波拉契数值为l3。请改正程序中的错误,使它能得出正确的结果。注意:部分源程序在文件MODll.C中,不得增行或删行,也不得更改程序的结构。
 正确答案:
正确答案:
【参考答案】去掉分号(2Casel:caBe2:returnl;【考点分析】本题考查:switch语句,其一般形式为switch(表达式)cage常量表达式l:语句l;case常量表达式2:语句2;cm常量表达式n:语句n;default:语句n+1;其中switch(表达式)后不应该带有“;”,同时case语句常量后应该是“:”。【解题思路】C语言中,switch语句之后不能有分号,并且case语句常量后应用的是冒号。 -
第5题:
下列给定程序中函数fun的功能是:用递归算法计算斐波拉契数列中第n项的值。从第1项起,斐波拉契数列为:1、1、2、3、5、8、13、21、…… 例如,若给n输入7,则该项的斐波拉契数值为13。 请改正程序中的错误,使它能得出正确结果。 注意:部分源程序在文件MODll.C中,不得增行或删行,也不得更改程序的结构。

 正确答案:
正确答案:
(1)去掉分号
(2)case l:case 2:return l;
【考点分析】
本题考查:switch语句,其一般形式为:
switch(表达式){
case常量表达式1:语句l;
case常量表达式2:语句2;
case常量表达式n:语句n;

其中switch(表达式)后不应该带有”;”,同时case语句常量后应该是”:“。
【解题思路】
c语言中,sw迎ch语句之后不能有分号,并且case语句常量后应用的是冒号。 -
第6题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵()。从而,f(n+1),f(n)=(f(2),f(1))*(65).A.An-1
B.An
C. An+1
D. An+2答案:A解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第7题:
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】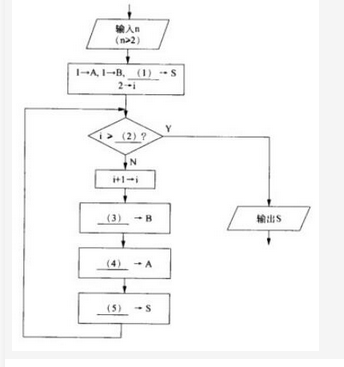 答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
【解析】
菲波那契数列的特点是首2项都是1,从第3项开始,每一项都是前两项之和。该数列的前几项为1,1,2, 3,5,8,…。在流程图中,送初始值1—A,2—B后,显然前2项的和S应等于2,所以(1)处应填2 (或A+B)。此时2→i (i表示动态的项编号),说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和,循环可以结束了。因此(2)处填n。判断框中用“>”或“≥”的效果是一样的,因为随着i的逐步增1,只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些,以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1,继续往下计算。原来的前两项值(分别在变量A和B中)将变更成新的前两项再放到变量A和B中。
首先可以用A+B—B实现(原A) + (原B)—(新B),因此(3)处填A+B。为了填新A值(原来的B值),不能用B—A,因为变量B的内容已经改变为(原A) + (原B),而B-A正是((原A) + (原B))-(原A)=(原B),因此可以用B-A—A来实现新A的赋值。这样,(4)处填B-A。最后应是前n项和值的累加(比原来的S值增加了新B值),所以(5)处应填S+B。填完各个空后,最好再用具体的数值来模拟流程图走几个循环检查所填的结果(这是防止逻辑上出错的好办法)。 -
第8题:
自然界中存在丰富的斐波那契数列,斐波那契数列来源于一个古老的数学问题,是由12世纪意大利数学家斐波那契在其书中所产生的。斐波那契数列和黄金分割的关系是?()
- A、黄金比例是斐波那契数列中的一项
- B、斐波那契数列相邻两项的比例逐渐逼近黄金比例
- C、黄金分割是指用斐波那契数列对一个量进行分割
- D、黄金比例是斐波那契数列的别名
正确答案:B -
第9题:
数据结构里,递归问题的解决都要靠栈来完成,以下可以递归实现的有()。
- A、斐波那契数列
- B、n!(n的阶乘)
- C、汉诺塔问题
- D、n的k次幂
正确答案:A,B,C,D -
第10题:
在1,1,2,3,5,8,13,21,34……这一斐波那契数列中,第12项是()。
- A、143.0
- B、144.0
- C、145.0
- D、146.0
正确答案:B -
第11题:
下面数列体现斐波那契特点的是()
- A、1、1、2、3、5、8、13、21、……
- B、2、3、5、8、13、21、……
- C、2、4、6、8、10、……
- D、1、1、2、4、6、8、……
正确答案:A -
第12题:
多选题汉诺塔问题可以用递归解决,以下也可用递归实现的是()A求1-n的和
B求n的阶乘
C斐波那契数列
Dn^k(^表示幂)
正确答案: C,D解析: 暂无解析 -
第13题:
计算斐波那契数列第n项的函数定义如下: intfib(intn){ if(n==0)returnl; elseif(n==l)return2: elsereturnfib(n-1)+fib(n-2); } 若执行函数调用表达式fib(2),函数fib被调用的次数是( )。
A.1
B.2
C.3
D.4
正确答案:C
C。【解析】针对递归调用的含义。当n为2时有fib(o),fib(1),fib(2)被调用,且fib(O),fib(1)时调用结束,即共3次。 -
第14题:
已知数列的递推公式如下:
f(n)=1 当n=0,1时
f(n)=f(n-1)+f(n-2) 当n>1时
则按照递推公式可以得到数列:1,1,2,3,5,8,13,21,34,55,……。现要求
从键盘输入n值,输出对应项的值。例如当输入n为8时,应该输出34。程序如下,
请补充完整。
Private Sub runll_Click()
f0=1
f1=1
num=Val(InputBox("请输入一个大于2的整数:"))
For n=2 To 【 】
f2=【 】
f0=f1
f1=f2
Next n
MsgBox f2
End Sub
正确答案:num f0+f1
num f0+f1 解析:程序首先需要接受用户输入的值,根据程序代码可以判断,使用变量num来存放用户输入的值,使用循环实现递推,根据题面“要求从键盘输入n值,输出对应项的值”,可知循环从2开始,到用户输入的值结束,也就是“Forn=2 To num”。根据题面给出的公式“当n>1时,f(n)=f(n-1)+f(n-2)”,可知第n项的值总等于它前两项(即第n-2项与第n-1项)之和,在程序For循环中,总用f2表示第n项,f0表示第n-2项,f1表示第n-1项,所以f2=f0+f1。 -
第15题:
计算斐波那契数列第n项的函数定义如下: intfib(intn){ if.(n==0)return1; elseif(n==1)return2: elsereturnfib(n-1)+fib(n-2); } 若执行函数调用表达式fib(2),函数fib被调用的次数是( )。
A.1
B.2
C.3
D.4
正确答案:C
C。【解析】根据递归调用的含义,当n为2时有fib(o),fib(1),fib(2)被调用,且fib(0),fib(1)时调用结束,共3次。 -
第16题:
请在函数proc()的横线上填写若干表达式,使从键盘上输入一个整数n,输出斐波那契数列的前n个数。斐波那契数列是一个整数数列,该数列自第3项开始,每个数等于前面两个数之和,即0,1,1,2,3,5,8,13,21,34,55,…
注意:部分源程序给出如下。
请勿改动main()函数和其他函数中的任何内容,仅在函数proc()的横线上填入所编写的若干表达式或语句。
试题程序:

 正确答案:
正确答案:【1】n==0【2】n==1【3】proc(n-1)+proc(n-2)
【解析】由斐波那契数列的定义可知,该数列中有两个特殊项。当n为0时,其值为0;当n为1时,其值为1。因此,【1】处填“n==0”;【2】处填“n==1”;当n为其他值时,为前两项的和,因此,[3]处填“proc(n-1)+proc(n-2)”。 -
第17题:
菲波那契(Fibonacci)数列定义为 f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出,n>1时,有向量的递推关系式: (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵( )。从而,(f(n+1),f(n)=(f(2),f(1))*( )
A.
 B.
B. C.
C. D.
D. A.An-1B.AnC.An+1D.An+2正确答案:D,A
A.An-1B.AnC.An+1D.An+2正确答案:D,A
-
第18题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵(64)。从而,f(n+1),f(n)=(f(2),f(1))*(65).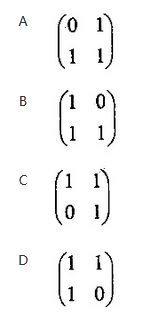 答案:D解析:本题考查数学应用的基础知识。
答案:D解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第19题:
汉诺塔问题可以用递归解决,以下也可用递归实现的是()
- A、求1-n的和
- B、求n的阶乘
- C、斐波那契数列
- D、n^k(^表示幂)
正确答案:A,B,C,D -
第20题:
“0,1,1,2,3,5,8,13,21”这个著名数列名为?()
- A、大衍数列
- B、斐波那契数列
- C、陈景润数列
- D、卢卡斯数列
正确答案:B -
第21题:
卢卡斯数列是斐波那契数列的推广,其前两项是()
- A、1、2
- B、1、1
- C、2、3
- D、1、3
正确答案:D -
第22题:
下面()组数列是斐波那契数列。
- A、1,1,2,3,5,8,13,21,34,55,„„
- B、1,2,3,4,5,6,7,8,9,10,11,„„
- C、1,2,4,8,10,20,40,80,160,320„
正确答案:A -
第23题:
单选题数据结构与算法里,设fun(n)表示斐波那契数列的第n项的值,fun是函数名,n是整型参数,那么根据递归思想它应等于()。Afun(n)+fun(n-1)
Bfun(n-1)+fun(n-2)
Cfun(n-1)*fun(n-2)
Dfun(n-2)+fun(n-3)
正确答案: D解析: 暂无解析 -
第24题:
单选题在1,1,2,3,5,8,13,21,34……这一斐波那契数列中,第12项是()。A143.0
B144.0
C145.0
D146.0
正确答案: D解析: 暂无解析
