一质点在xOy平面内运动，运动方程为 x = 2t， y = 19-2t2 式中x，y以m计，t以s计。（1）计算质点的运动轨道；（2）求t=1s及t=2s时质点的位置矢量，并求此时间间隔内质点的平均速度；（3）求t=1s及t=2s时质点的瞬时速度和瞬时加速度；（4）在什么时刻，质点的位置矢量正好与速度矢量垂直？此刻，它们的x，y分量各为多少？（5）在什么时刻，质点距原点最近？最近距离是多少？

题目

相似考题

1.若一个5kg质量的质点沿着平面轨道运动,轨道方程为r=(2t＋10)和 , t的单位为秒,求t=2s时,作用在质点上的不平衡力的大小()A. 190NB. 200NC. 210ND. 220N

2.质点沿任意曲线运动,t时刻质点的极坐标为p(t)=beac,θ(t)=ct,试求此时刻质点的速度、加速度,并写出质点运动的轨道方程,式中α、b和c都是常量。

3.一质点沿直线运动，其运动方程为x=2+4t-2t2(SI)，在t从0到3s的时间间隔内，质点的位移大小为（）A．10mB．8mC．6mD．4m

4.质点从t=0时刻开始由静止沿x轴运动，其加速度a=2ti(SI)，则当t=2s时该质点的速度大小为________m／s.

更多“一质点在xOy平面内运动，运动方程为 x = 2t， y = 19-2t2 式中x，y以m计，t以s计。（1）计算质点的运动轨道；（2）求t=1s及t=2s时质点的位置矢量，并求此时间间隔内质点的平均速度；（3）求t=1s及t=2s时质点的瞬时速度和瞬时加速度；（4）在什么时刻，质点的位置矢量正好与速度矢量垂直？此刻，它们的x，y分量各为多少？（5）在什么时刻，质点距原点最近？最近距离是多少？”相关问题

第1题：

一质点沿x轴正方向运动，的规律变化，式中k是正常数。当t=0时，质点位于原点0处。求该质点的速度及加速度随时间t的变化规律。

答案：
解析：
第2题：

一质点沿x轴运动，其坐标与时间的变化关系为x=4t-2t3，式中x，t分别以m，s为单位，试计算：
(1)在最初2s内的位移和平均速度；
(2)2s末的瞬时速度：
(3)3S末的瞬时加速度。

答案：
解析：
第3题：

质点做直线运动的位移x与时间t的关系为x＝5t＋t²；（各物理量均采用国际制单位），则该质点（）
- A、第1s内的位移是5m
- B、前2s内的平均速度是6m/s
- C、任意相邻的1s内位移差都是1m
- D、任意1s内的速度增量都是2m/s
正确答案:D
第4题：

一质点沿直线Ox方向作加速运动，它离开O点的距离x随时间t变化的函数关系为x=5+2t3（m），该质点在t=0到t=2s时间段的平均速度为（）
- A、12m/s
- B、10.5m/s
- C、24m/s
- D、8m/s
正确答案:D
第5题：

一质点沿直线Ox方向做变速运动，它离开O点的距离x随时间变化的关系为x＝5＋2t³（m），它的速度随时间t变化的关系为v＝6t²（m/s），该质点在t＝0到t＝2s间的位移为（）m；t＝2s到t＝3s间的平均速度为（）m/s。

正确答案:16；38
第6题：

质点做直线运动的位移s与时间t的关系为s＝5t＋t²（各物理量均采用国际单位制单位），则该质点（）
- A、第1s内的位移是6m
- B、第2s末的瞬时速度是6m/s
- C、任意1s内的速度增量都是1m/s
- D、任意1s内的速度增量都是2m/s
正确答案:A,D
第7题：

某质点做直线运动的位移x与时间t的关系为x=3t+t²（各物理量均采用国际单位），则该质点（）
- A、第1s内的位移是3m
- B、任意1s内的速度增量都是2m/s
- C、前2s内的平均速度是6m/s
- D、任意相邻的ls内位移之差都是1m
正确答案:B
第8题：

一质点沿x轴运动V=1+3t²（m/s）。若t=0时，质点位于原点，则t=2s时，质点加速度的大小a=（），质点的坐标X=（）。

正确答案:12m/s^-1；10m
第9题：

一个质点由静止开始作直线运动，第1s内加速度为5m/s²，第2s内加速度为-5m/s²，第3s、第4s重复第1s、第2s内的情况，如此不断地运动下去，当经过时间为100s时，这个质点的位移是多少？当质点的位移达到56.25m时，质点经过了多少时间？

正确答案: 250m
22.7s
第10题：

一质点在Oxy平面内运动。运动学方程为x=2t和y=19-2t2（SI），则在第2秒末的瞬时速度大小v₂=（）
- A、6.32m/s。
- B、8.25m/s。
- C、5m/s。
- D、6m/s。
正确答案:B
第11题：

质点运动方程x=t²+2t-3，x以米计，t以秒计，则该质点2秒末的速度v=（）；加速度a=（）。

正确答案:6m/s；2m/s²
第12题：

一质点沿直线运动，运动方程为x（t）= 6²t-2³t．试求：（1）第2s内的位移和平均速度；（2）1s末及2s末的瞬时速度，第2s内的路程；（3）1s末的瞬时加速度和第2s内的平均加速度。

正确答案: （1）质点在第1s末的位置为：x（1）=6×1²-2×1³=4（m），
在第2s末的位置为：x（2）=6×2²-2×2³=8（m），
在第2s内的位移大小为：Δx=x（2）–x（1）=4（m），
经过的时间为Δt=1s，所以平均速度大小为：v=Δx/Δt=4（m·s^-1）。
（2）质点的瞬时速度大小为：v（t）=dx/dt=1²t-6²t，
因此v（1）=12×1-6×1²=6（m·s^-1），v（2）=12×2-6×2²=0
质点在第2s内的路程等于其位移的大小，即Δs=Δx=4m。
（3）质点的瞬时加速度大小为：a（t）=dv/dt=12-12t，
因此1s末的瞬时加速度为：a（1）=12-12×1=0，
第2s内的平均加速度为：a=[v（2）-v（1）]/Δt=[0–6]/1=-6（m·s^-2）。
第13题：

一质点沿半径R=1．6m的圆周运动，t=0时刻质点的位置为θ=0，质点的角速度w0=3．14s-1．若质点角加速度a=1．24t s-2。求：t=2．00 s时质点的速率、切向加速度和法向加速度。

答案：
解析：
角速度；切向加速度；法向加速度。根据角速度公式，质点在t=2s时的角速度为：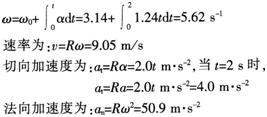
第14题：

质点做直线运动的位移x与时间t的关系为x=3t+2t²（各物理量均采用国际单位制单位），则该质点（）
- A、第2s内的位移是10m
- B、前3s内的平均速度是7m/s
- C、任意相邻1s内的位移差都是4m
- D、任意1s内的速度增量都是3m/s
正确答案:C
第15题：

一质点沿ox轴正方向运动的运动方程是x=t³-2t²+t+5，经过2s后它瞬时速度（），瞬时加速度是（）

正确答案:5m·s^-1；8m·s^-2
第16题：

质点做直线运动的位移x与时间t的关系为x=5t+t2（各物理量均采用国际单位制单位），则改质点（）
- A、第1s内的位移是5m
- B、前2s内的平均速度是6m/s
- C、任意相邻的1s内位移差都是1m
- D、任意1s内的速度增量都是2m/s
正确答案:D
第17题：

质点做直线运动的位移x与时间t的关系为x=5t+t2（各物理量均采用国际单位），则该质点（）
- A、第1s内的位移是5m
- B、前2s内的平均速度是6m/s
- C、任意1s内的速度增量都是2m/s
- D、任意相邻的ls内位移差都是1m
正确答案:C
第18题：

质点做直线运动的位移x与时间t的关系为x=5t＋2t²（各物理量均采用国际单位制单位，该质点（）
- A、初速度为5m/s
- B、前2s内的平均速度是6m/s
- C、任意相邻的1s内位移差都是4m
- D、任意1s内的速度增量都是2m/s
正确答案:A,C
第19题：

一质点沿x轴作直线运动，它的运动学方程为x=3+5t+6t²t³（SI），则加速度为零时，该质点的速度u=（）

正确答案:17m/s
第20题：

一质点沿直线Ox方向做变速运动，它离开O点的距离x随时间变化的关系为x=5+2t³（m），它的速度随时间t变化的关系为v=6t²（m/s），该质点在t=0到t=2s间的平均速度和t=2s末的瞬时速度的大小分别为（）
- A、12m/s，24m/s
- B、8m/s，24m/s
- C、12m/s，19.5m/s
- D、8m/s，13m/s
正确答案:B
第21题：

一质点沿x轴运动，其运动方程为x=5t-3t³，其中t以s为单位。当t=2s时，该质点正在（）
- A、加速
- B、减速
- C、匀速
- D、静止
正确答案:A
第22题：

一质点沿x方向运动，其加速度随时间变化关系为：a=3+2t，如果初始时刻质点的速度v₀为5m/s，则当ｔ为3s时，质点的速度（）

正确答案:v=23m/s
第23题：

一质点沿x方向运动，其加速度随时间变化关系为a=3+2t，（SI）如果初始时质点的速度v₀为5m/s，则当t为3s时，质点的速度v=（）。

正确答案:23m/s
第24题：

质点沿x方向运动，其加速度随时间的变化关系为a=3+2t（SI），如果初始时刻质点的速度v0为5m·s^-1，则当t为3s时，质点的速度v=（）。

正确答案:23m·s^-1

题目

相似考题

相关内容