在研究导热问题时需要通过边界条件来求解温度场，其中规定了边界上的温度值为：__________。A．第一类边界条件B．第二类边界条件C．第三类边界条件D．第四类边界条件

题目

在研究导热问题时需要通过边界条件来求解温度场，其中规定了边界上的温度值为：__________。

A．第一类边界条件

B．第二类边界条件

C．第三类边界条件

D．第四类边界条件

相似考题

1.关于薄板内力,下列叙述错误的是()。A、薄板内力，是薄板横截面上的内力。B、薄板内力等于每单位宽度的横截面上(δ×1)的弯矩。C、薄板通过求解内力进行设计设计。D、在板边(小边界)上，要用内力的边界条件代替应力的边界条件。

2.第一类边界条件下，常物性稳态导热大平壁，其温度分布与导热系数无关的条件是()。A.无内热源B.内热源为定值C.负内热源D.正内热源

3.规定了边界上的热流密度值，称为()。A、第二类边界条件B、第一类边界条件C、第三类边界条件D、与边界条件无关

4.按应力求解平面问题时,应力分量必须满足()。A、在区域内的平衡微分方程B、在区域内的相容方程C、在边界上的应力边界条件D、对于多连体，须满足位移的单值条件

更多“在研究导热问题时需要通过边界条件来求解温度场，其中规定了边界上的温度值为：__________。”相关问题

  • 第1题：

    不计体力,在极坐标中按应力求解平面问题时,应力函数必须满足( )①区域内的相容方程;②边界上的应力边界条件;③满足变分方程; ④如果为多连体,考虑多连体中的位移单值条件。

    A. ①②④

    B. ②③④

    C. ①②③

    D. ①②③④


    参考答案A

  • 第2题：

    求解导热微分方程需要给出单值性条件，下列选项中哪一组不属于单值性条件？（　　）。

    A． 边界上对流换热时空气的相对湿度及压力
    B． 几何尺寸及物性系数
    C． 物体中的初始温度分布及内热源
    D． 边界上的温度梯度分布

    答案：A
    解析：
    单值性条件包含初始条件、边界条件、几何条件和物理条件。边界条件分为三类，第一类边界条件规定了边界上的温度值；第二类边界条件规定了边界上的热流密度值；第三类边界条件规定了边界面与流体间的换热系数和流体的温度。B项属于单值性条件中的几何条件和物理条件，C项属于单值性条件中的初始条件，D项属于单值性条件中的边界条件，而A项不属于单值性条件中的初始条件、边界条件、几何条件和物理条件任意一项，因此答案为A。

  • 第3题：

    根据常热流密度边界条件下半无限大物体的非稳态导热分析解，渗透厚度δ与导热时间τ的关系可以表示为（　　）。（其中α为热扩散系数，c为常数）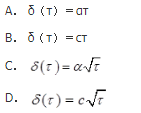


    答案：D
    解析：
    对于常热流密度边界条件下的非稳态导热，其热渗透厚度δ满足：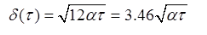

    其中α是物质的热扩散系数，为常数，则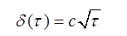

  • 第4题：

    导热基本定律适用于（）。

    • A、稳定温度场
    • B、单向度温度场
    • C、多向度温度场
    • D、各种温度场

    正确答案:D

  • 第5题：

    用分离变量法直接求解非稳态导热问题时，以下叙述中不正确的有（）

    • A、初始条件必须是齐次的
    • B、必须采用常物性假定
    • C、边界条件必须是齐次的
    • D、微分方程必须是齐次的

    正确答案:D

  • 第6题：

    导热问题的第二类边界条件是（）

    • A、已知物体边界上的温度分布
    • B、已知物体表面与周围介质之间的换热情况
    • C、已知物体边界上的热流密度
    • D、已知物体边界上流体的温度与流速

    正确答案:C

  • 第7题：

    对于第一类边界条件的稳态导热问题，其温度分布不导热系数有没有关系？


    正确答案:寻热问题的完整数学描述包括寻热微分方程和定解条件。在寻热系数为常数的稳态寻热问题中，只有第一类边界条件下的无内热源稳态寻热问题的分析解才不寻热系数没有关系， 即寻热系数只影响热流量，而不影响温度场。

  • 第8题：

    对于无限大平板内的一维导热问题，试说明在三类边界条件中，两侧边界条件的哪些组合可以使平板中的温度场获得确定的解？


    正确答案:两侧面的第一类边界条件；一侧面的第一类边界条件和第二类边界条件；一侧面的第一类边界条件和另一侧面的第三类边界条件；一侧面的第一类边界条件和另一侧面的第三类边界条件。

  • 第9题：

    问答题
    简单归纳一下导热问题中常见的几类边界条件以及其定义。

    正确答案： 导热问题主要有以下三类边界条件：（１）第一类边界条件：该条件是给定系统边界上的温度分布，它可以是时间和空间的函数，也可以为给定不变的常数值。（2）第二类边界条件：该条件是给定系统边界上的温度梯度，即相当于给定边界上的热流密度，它可以是时间和空间的函数，也可以为给定不变的常数值。（3）第三类边界条件：该条件是第一类和第二类边界条件的线性组合，常为给定系统边界面与流体间的换热系数和流体的温度，这两个量可以是时间和空间的函数，也可以为给定不变的常数值。
    解析： 暂无解析

  • 第10题：

    单选题
    导热问题的第二类边界条件是（）
    A

    已知物体边界上的温度分布

    B

    已知物体表面与周围介质之间的换热情况

    C

    已知物体边界上的热流密度

    D

    已知物体边界上流体的温度与流速


    正确答案： A
    解析： 暂无解析

  • 第11题：

    问答题
    对于第一类边界条件的稳态导热问题，其温度分布不导热系数有没有关系？

    正确答案： 寻热问题的完整数学描述包括寻热微分方程和定解条件。在寻热系数为常数的稳态寻热问题中，只有第一类边界条件下的无内热源稳态寻热问题的分析解才不寻热系数没有关系， 即寻热系数只影响热流量，而不影响温度场。
    解析： 暂无解析

  • 第12题：

    单选题
    导热问题的常见边界条件可归纳为（）
    A

    两类

    B

    三类

    C

    四类

    D

    五类


    正确答案： A
    解析： 暂无解析

  • 第13题：

    导热问题的第二类边界条件是()

    A. 已知物体边界上的温度分布

    B. 已知物体边界上的热流密度

    C. 已知物体表面与周围介质之间的换热情况

    D.已知物体边界上流体的温度与流速


    参考答案C

  • 第14题：

    对于题13图中的二维稳态导热问题，右边界是恒定热流边界条件，热流密度为qw，若采用有限差分法求解，当Δx＝Δy时，则在下面的边界节点方程式中正确的是（　　）。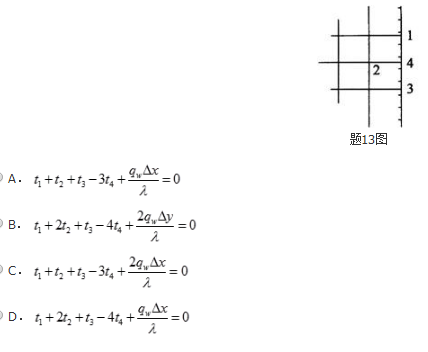


    答案：B
    解析：
    边界节点离散方程在第一类边界条件下，因边界节点的温度已给定，无需建立边界节点的方程，其温度值会进入到与之相邻的内节点方程中。对于第二及第三类边界条件，则必须建立边界节点的节点方程，从而使整个节点方程组封闭，利于求解。则根据题13图列节点4的热平衡方程：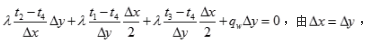

    整理上式得

  • 第15题：

    对于图中的二维稳态导热问题，右边界是恒定热流边界条件，热流密度为qw，如果采用有限差分法求解，当Δx=Δy时，则在下面的边界节点方程式中，哪一个是正确的？（　　）


    答案：D
    解析：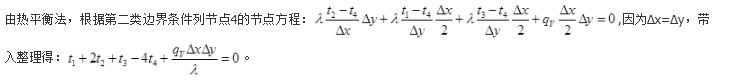

  • 第16题：

    一维无限大平壁的导热问题，两侧给定的均为第二类边界条件，能否求出其温度分布？为什么？


    正确答案: （1）一维无限大平壁的导热问题，两侧给定的均为第二类边界条件，不能求出其温度分布。
    （2）因为第二类边界条件所对应的是温度曲线的斜率，不绝对温度没有对应关系。

  • 第17题：

    为什么在主要边界（大边界）上必须满足精确的应力边界条件式（2-15），而在小边界上可以应用圣维南原理，用三个积分的应力边界条件（即主矢量、主矩的条件）来代替？如果在主要边界上用三个积分的应力边界条件代替式（2-15），将会发生什么问题？


    正确答案:弹性力学问题属于数学物理方程中的边值问题，而要使边界条件完全得到满足，往往比较困难。这时，圣维南原理可为简化局部边界上的应力边界条件提供很大的方便。将物体一小部分边界上的面力换成分布不同，但静力等效的面力（主矢、主矩均相同），只影响近处的应力分布，对远处的应力影响可以忽略不计。如果在占边界绝大部分的主要边界上用三个积分的应力边界条件来代替精确的应力边界条件（公式2-15），就会影响大部分区域的应力分布，会使问题的解答精度不足。

  • 第18题：

    简单归纳一下导热问题中常见的几类边界条件以及其定义。


    正确答案: 导热问题主要有以下三类边界条件：（１）第一类边界条件：该条件是给定系统边界上的温度分布，它可以是时间和空间的函数，也可以为给定不变的常数值。（2）第二类边界条件：该条件是给定系统边界上的温度梯度，即相当于给定边界上的热流密度，它可以是时间和空间的函数，也可以为给定不变的常数值。（3）第三类边界条件：该条件是第一类和第二类边界条件的线性组合，常为给定系统边界面与流体间的换热系数和流体的温度，这两个量可以是时间和空间的函数，也可以为给定不变的常数值。

  • 第19题：

    导热问题的常见边界条件可归纳为（）

    • A、两类
    • B、三类
    • C、四类
    • D、五类

    正确答案:B

  • 第20题：

    单选题
    导热基本定律适用于（）。
    A

    稳定温度场

    B

    单向度温度场

    C

    多向度温度场

    D

    各种温度场


    正确答案： C
    解析： 暂无解析

  • 第21题：

    问答题
    一维无限大平壁的导热问题，两侧给定的均为第二类边界条件，能否求出其温度分布？为什么？

    正确答案： （1）一维无限大平壁的导热问题，两侧给定的均为第二类边界条件，不能求出其温度分布。
    （2）因为第二类边界条件所对应的是温度曲线的斜率，不绝对温度没有对应关系。
    解析： 暂无解析

  • 第22题：

    问答题
    对于无限大平板内的一维导热问题，试说明在三类边界条件中，两侧边界条件的哪些组合可以使平板中的温度场获得确定的解？

    正确答案： 两侧面的第一类边界条件；一侧面的第一类边界条件和第二类边界条件；一侧面的第一类边界条件和另一侧面的第三类边界条件；一侧面的第一类边界条件和另一侧面的第三类边界条件。
    解析： 暂无解析

  • 第23题：

    单选题
    求解导热微分方程需要给出单值性条件，下列选项中哪一组不属于单值性条件？（　　）。[2017年真题]
    A

    边界上对流换热时空气的相对湿度及压力

    B

    几何尺寸及物性系数

    C

    物体中的初始温度分布及内热源

    D

    边界上的温度梯度分布


    正确答案： A
    解析：
    单值性条件包含初始条件、边界条件、几何条件和物理条件。边界条件分为三类，第一类边界条件规定了边界上的温度值；第二类边界条件规定了边界上的热流密度值；第三类边界条件规定了边界面与流体间的换热系数和流体的温度。B项属于单值性条件中的几何条件和物理条件，C项属于单值性条件中的初始条件，D项属于单值性条件中的边界条件，而A项不属于单值性条件中的初始条件、边界条件、几何条件和物理条件任意一项，因此答案为A。

  • 第24题：

    问答题
    为什么在主要边界（大边界）上必须满足精确的应力边界条件式（2-15），而在小边界上可以应用圣维南原理，用三个积分的应力边界条件（即主矢量、主矩的条件）来代替？如果在主要边界上用三个积分的应力边界条件代替式（2-15），将会发生什么问题？

    正确答案： 弹性力学问题属于数学物理方程中的边值问题，而要使边界条件完全得到满足，往往比较困难。这时，圣维南原理可为简化局部边界上的应力边界条件提供很大的方便。将物体一小部分边界上的面力换成分布不同，但静力等效的面力（主矢、主矩均相同），只影响近处的应力分布，对远处的应力影响可以忽略不计。如果在占边界绝大部分的主要边界上用三个积分的应力边界条件来代替精确的应力边界条件（公式2-15），就会影响大部分区域的应力分布，会使问题的解答精度不足。
    解析： 暂无解析

相关内容