甲、乙两单位共同举办新年文艺联欢会,设一、二等奖若干。已知,甲、乙两单位获奖人数的比为4∶3;甲、乙两单位获一等奖的人数之和占两单位获奖人数总和的40%。甲、乙两单位获一等奖的人数之比为3∶4,甲单位获一等奖的人数占该单位获奖总人数的A.50% B.45% C.40% D.30%
题目
甲、乙两单位共同举办新年文艺联欢会,设一、二等奖若干。已知,甲、乙两单位获奖人数的比为4∶3;甲、乙两单位获一等奖的人数之和占两单位获奖人数总和的40%。甲、乙两单位获一等奖的人数之比为3∶4,甲单位获一等奖的人数占该单位获奖总人数的
A.50%
B.45%
C.40%
D.30%
B.45%
C.40%
D.30%
相似考题
更多“甲、乙两单位共同举办新年文艺联欢会,设一、二等奖若干。已知,甲、乙两单位获奖人数的比为4∶3;甲、乙两单位获一等奖的人数之和占两单位获奖人数总和的40%。甲、乙两单位获一等奖的人数之比为3∶4,甲单位获一等奖的人数占该单位获奖总人数的 ”相关问题
-
第1题:
甲、乙两单位共同举办新年文艺联欢会,设一、二等奖若干。已知,甲、乙两单位获奖人数的比为4∶3;甲、乙两单位获一等奖的人数之和占两单位获奖人数总和的40%。甲、乙两单位获一等奖的人数之比为3∶4,甲单位获一等奖的人数占该单位获奖总人数的
A.50%
B.45%
C.40%
D.30%
正确答案:D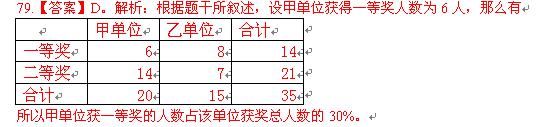
-
第2题:
某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8,分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3,乙科室为5∶2。则丙科室男女员工人数之比为:A.1∶2
B.2∶3
C.5∶9
D.5∶8答案:C解析:第一步,本题考查基础应用题,用赋值法解题。
第二步,根据男女比为15∶13,则总人数应该为28的倍数;又因为甲∶乙∶丙=5∶7∶8,则总人数应该为20的倍数;所以赋值总人数为140,则男生人数为75,女生人数为65。甲=35,乙=49,丙=56。又因为甲科室的男女比为4∶3,则甲的男生为20,甲的女生为15,又因为乙科室的男女比为5∶2,则乙的男生为35,乙的女生为14,所以得出丙的男生为75-20-35=20,丙的女生为65-15-14=36,则丙的男女比=20∶36=5∶9。 -
第3题:
甲、乙两车间原有人数的比为4:3,甲车间调12人到乙车间后,甲、乙两车间的人数变为2:3,甲车间原有人数是( ).A.18人
B.35人
C.40人
D.144人答案:C解析:
以甲车间原有40人.
另解,甲、乙两车间原来人数之比为4:3=20:15,调整后人数之比为2:3=14:21,可知甲车间减少了20-14=6份=12人,每份2人,则甲车间原有20×2=40人. -
第4题:
某次作文竞赛设优胜奖和新人奖。已知:(1)新兴小学和红梅小学两校获奖的人数比为6 :5。(2)新兴小学、红梅小学两校获新人奖的人数总和占两校获奖人数总和的60%。 (3)新兴小学、红梅小学两校获新人奖的人数之比为5 : 6。问新兴小学校获新人奖的人数占该校获奖总人数的比重是多少?( )A. 20%
B. 30%
C. 50%
D. 60%答案:C解析:已知新兴小学、红梅小学两校获新人奖的人数之比为5 :6,那么设新兴小学获新人奖的人数为5份,红梅小学为6份。因为新人奖的人数占两校获奖人数总和的60%,那么新兴小学获新人奖的人数占获奖总人数的 又因为新兴小学、红梅小学两学校获奖的人数比为6 : 5,所以设总人数为11份,新兴小学得奖的人数占其中6份。可知新兴小学获新人奖者占该校获奖总人数的比重为
又因为新兴小学、红梅小学两学校获奖的人数比为6 : 5,所以设总人数为11份,新兴小学得奖的人数占其中6份。可知新兴小学获新人奖者占该校获奖总人数的比重为
-
第5题:
某单位有甲和乙两个人数相同的处室,甲处室党员人数是群众人数的1.5倍,而两个处室党员总人数与群众总人数正好相同。现从甲处室调走10名党员后,甲处室和乙处室党员占各自处室现有职工的比例相同。则两个处室最初共有多少人?A.48
B.60
C.72
D.90答案:B解析:第一步,本题考查方程问题。第二步,甲乙两个处室人数相同,甲党员和群众人数之比为3:2,所以乙党员和群众人数之比 为2:3,设甲党员和群众人数分别为3x和2x,所以(3x-10):2x=2:3,可得,x=6,所以总人数为2×5x=10x=60。因此,选择B选项。 -
第6题:
甲、乙两个单位人数相同,甲单位的党员占总人数的20%,乙单位的党员占总人数的25%。如果乙单位20名党员与甲单位20名群众互换单位,则两个单位党员占比相同。问两个单位共有党员多少人?( )A.256
B.288
C.324
D.360答案:D解析:
第一步,本题考查基础应用题,用方程法解题。
第二步,设甲、乙两个单位的总人数均为20x,那么甲单位的党员人数为4x,乙单位的党员人数为5x,乙单位20名党员与甲单位20名群众互换单位后,甲单位党员人数为4x+20,乙单位党员人数为5x-20,总人数固定,两单位党员占比相同则党员人数相同,可列方程:4x+20=5x-20,解得x=40,那么两个单位共有党员4x+5x=9x=360(名)。 -
第7题:
甲乙两个办公室的员工都不到20人,如果从甲办公室调到乙办公室若干人,则甲的人数是乙的人数的2倍;如果乙调到甲办公室相同的人数,则甲的人数就是乙的3倍,则原来甲办公室有多少人?A. 16
B. 17
C. 18
D. 19答案:B解析:设甲为x,乙为y,甲调到乙人数为z。有方程组:x-z=2(y+z),x+z=3(y-z),消去z整理得:7x=17y,则x:y=17:7,由于人数不到20人,则甲为17人。答案为B选项。 -
第8题:
某单位人员招聘共设三类职位,规定每人限报两类职位。现报名人数为63人,每人均报了职位,甲、乙、丙三类岗位报名人数分别为40、31、28,同时报甲和乙类职位人数为13,同时报甲和丙两类职位的人数为15人,则同时报乙和丙类职位人数为:A.8
B.6
C.7
D.9答案:A解析:第一步,本题考查容斥问题,属于三集合容斥类。
第二步,设同时报乙和丙类岗位的人数为x,三集合标准型核心公式:总数-都不满足的=集合A+集合B+集合C-A∩B-B∩C-A∩C+都满足的,代入数值即40+31+28-13-15-x=63,解得x=8。 -
第9题:
总公司派出若干人员组成5个工作组到下属公司进行巡查。其中,甲组的人数是总人数的14%,乙组人数是总人数的1/4,丙组人数是甲乙两组人数之和的2/3,丁组人数是甲丙两组人数之差的2倍,且其中有三个组的人数正好是连续的偶数,问甲组比戊组多多少人?A.4
B.6
C.10
D.18答案:B解析:第一步,本题考查基础应用题。
第二步,甲组的人数是总人数的14%,乙组人数是总人数的 },即25%;丙组人数是甲乙两组人数之和的{图1,即(14%+25%)×
},即25%;丙组人数是甲乙两组人数之和的{图1,即(14%+25%)×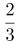 =26%;丁组人数是甲丙两组人数之差的2倍,即(26%-14%)×2=24%;可得戊人数为1-14%-25%-26%-24%=11%。根据占比,可知人数正好是连续偶数的三个组分别为丁24%、乙25%、丙26%,由倍数特性可知,总人数应为200,得丁组48人、乙组50人、丙组52人满足条件。
=26%;丁组人数是甲丙两组人数之差的2倍,即(26%-14%)×2=24%;可得戊人数为1-14%-25%-26%-24%=11%。根据占比,可知人数正好是连续偶数的三个组分别为丁24%、乙25%、丙26%,由倍数特性可知,总人数应为200,得丁组48人、乙组50人、丙组52人满足条件。
第三步,甲组比戊组多200×(14%-11%)=6(人)。
因此,选择B选项。 -
第10题:
甲、乙两个单位共同研发出一项技术成果,甲单位声明放弃该技术成果的专利申请权,乙单位单独申请并获得了该项技术成果的专利权。下列说法正确的是()。A.甲单位有权免费实施该专利
B.甲单位有权要求乙单位给予补偿
C.乙单位转让该专利时应当征得甲单位同意
D.乙单位转让该专利时,甲单位享有优先受让权答案:A解析:(1)合作开发的当事人一方声明放弃其共有的专利申请权的,可以由另一方单独申请;申请人取得专利权的,放弃专利申请权的一方可以免费实施该专利。(2)如果转让专利“申请权”,他方享有以同等条件优先受让的权利。 -
第11题:
单选题某企业在软件园区的分公司有甲、乙两个开发团队,先从乙团队调走25人,此时甲、乙团队人数比为4:3,然后又从甲团队调走42人,此时甲、乙团队人数比为2:5,则两次调动前甲、乙团队人数比为:A3:4
B6:7
C1:2
D2:5
正确答案: A解析: -
第12题:
单选题某企业在软件园区的分公司有甲、乙两个开发团队,先从乙团队调走25人,此时甲、乙团队人数比为4:3.然后又从甲团队调走42人,此时甲、乙团队人数比为2:5,则两次调动前甲、乙团队人数比力:A3:4
B6:7
C1:2
D2:5
正确答案: B解析: -
第13题:
某公司l00名员工对甲、乙两名经理进行满意度评议,对甲满意的人数占全体参加评议员工的3/5,对乙满意的人数比甲的人数多6人,对甲、乙都不满意的占都满意人数的1/3多2人,则对甲、乙都满意的人数是多少人?
A.36
B.26
C.48
D.42
正确答案:D
-
第14题:
为方便值班轮休,现将甲、乙两组奥运志愿者服务队拆分成3组,原甲组人数的1/3加乙组人数的+值早班;原甲组人数的1/4与乙组人数的1/3值中班;两组剩下共25人值晚班。假定每人每天只值一班,则甲、乙两组原来共有()人。A.42
B.48
C.60
D.72答案:C解析: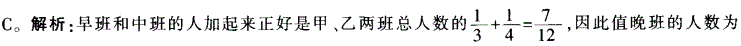
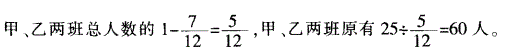
-
第15题:
甲、乙两个单位分别有60和42名职工,共同成立A、B两个业余活动小组,所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%,乙单位职工中参加B组的人数与参加A组的人数之比为3∶4,参加B组的人中,甲单位职工占5/8。问有多少人仅参加A组?A.35
B.42
C.46
D.56答案:C解析:第一步,本题考查容斥问题。
第二步,设乙单位只参加一个小组的人数为5x,则只参加A组的有5x·60%=3x名职工,那么只参加B组的有5x-3x=2x名职工,设乙单位AB组都参加的有y人。可列方程:(2x+y)∶(3x+y)=3∶4,解得x=y,那么乙单位中参加B组的有3x人,参加A组的有4x人,AB都参加的有x人,可列方程:3x+4x-x=42,解得x=7,那么参加B组的有21人,只参加A组的有21人。
那么甲单位只参加A组的有60-35=25(人),那么两个单位只参加A组的有21+25=46(人)。 -
第16题:
某单位有甲、乙两个部门,若从甲部门调动7个人到乙部门,则乙部门的人数比甲部门的 人数多2倍,若从乙部门调动5个人到甲部门,则甲、乙两部门人数相等,问甲部门有多少 人?( )A. 12
B. 15
C. 17
D. 19答案:D解析:
-
第17题:
已知甲校学生人数是乙校学生人数的40%,甲校女生人数是甲校学生人数的30%,乙校 男生人数是乙校学生人数的42%,那么,两校女生总数占两校学生总数的( )。
A. 30%
B. 50%
C. 40%
D. 60%答案:B解析:设甲校有200人,则乙校有200 ÷ 40% = 500 (人),甲校女生有 200×30% = 60(人),乙校有女生500×(1 —42%) = 290(人),两校女生共350人,两校学生共 700人,所以女生总数占50%。 -
第18题:
某企业在软件园区的分公司有甲、乙2个开发团队。现从乙团队调走25人,此时甲、乙团队人数比为4∶3。然后又从甲团队调走42人,此时甲、乙团队人数之比2∶5。问两次调动之前,甲、乙团队人数比为:A.3∶4
B.6∶7
C.1∶2
D.2∶5答案:B解析:第一步,本题考查基础应用题。
第二步,设第一次调动后甲团队的人数为4x,则乙的人数为3x,根据第二次调动可得(4x-42)∶3x=2∶5,解得x=15。
第三步,在两次调动前,甲团队的人数是4×15=60(人),乙团队的人数是3×15+25=70(人),故甲、乙两队人数之比为6∶7。 -
第19题:
某市服务行业举行业务技能大赛,其中东区参赛人数占总人数的1/5,西区参赛人数占总人数的2/5,南区参赛人数占总人数的1/4,其余的是北区的参赛人员。结果东区参赛人数的1/3获奖,西区参赛人数的1/12获奖,南区参赛人数的1/9获奖,已知参赛总人数超过100人,不到200人,则参赛总人数为( )。A.120
B.140
C.160
D.180答案:D解析:第一步,根据“占”、“超过”、“不到”等,判断此题是约数倍数问题,采用倍数特性法。第二步,由于人都是整数,所以由“东区参赛人数占总人数的1/5”、“东区参赛人数的1/3”,可知东区人数是3的倍数,总人数是15的倍数;同理,由西区人数推知总人数是12×5/2=30的倍数、由南区人数推知总人数是4×9=36的倍数。因此总人数是15、20、36的最小公倍数180的倍数。第三步,由“超过100人不到200人”,此区间180的倍数只有180一个,那么总人数即180人。因此,选择D选项。 -
第20题:
甲、乙两单位签订了建设工程合同,但甲单位因丙单位的原因使合同迟延履行,则( )。A:甲单位应向乙单位承担违约责任
B:丙单位应向乙单位承担违约责任
C:甲、乙两单位均可向丙单位提出索赔
D:乙单位无权解除合同答案:A解析:2019版教材P57
因第三人原因造成违约时违约责任的承担。当事人一方因第三人的原因造成违约的,应当向对方承担违约责任。当事人一方和第三人之间的纠纷,依照法律定或者依照约定解决。因而,正确选项为A。 -
第21题:
某公司共有甲、乙两个部门.如果从甲部门调10人到乙部门,那么乙部门人数是甲部门人数的2倍;如果把乙部门员工的1/5调到甲部门,那么两个部门的人数相等.该公司的总人数为A.150
B.180
C.200
D.240
E.250答案:D解析:
-
第22题:
根据重复抽样的资料,甲单位工人工资方差为25,乙单位为100,乙单位人数比甲单位多3倍,则抽样平均误差()。
- A、甲单位较大
- B、无法判断
- C、乙单位较大
- D、相同
正确答案:C -
第23题:
单选题三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数?( )A48人
B49人
C50人
D51人
正确答案: A解析:
设甲单位有x人,则乙单位有(x+2)人,丙单位有(x+x+2-20)人,由题意得,x+x+2+(x+x+2-20)=180,得x=49人。 -
第24题:
单选题某企业在软件园区的分公司有甲、乙2个开发团队,现从乙团队调走25人,此时甲、乙团队人数比为4:3,然后又从甲团队调走42人,此时甲、乙团队人数比为2:5。问两次调动之前,甲、乙团队人数比为:A3:4
B6:7
C1:2
D2:5
正确答案: B解析:
