某企业在软件园区的分公司有甲、乙2个开发团队。现从乙团队调走25人，此时甲、乙团队人数比为4∶3。然后又从甲团队调走42人，此时甲、乙团队人数之比2∶5。问两次调动之前，甲、乙团队人数比为：A.3∶4 B.6∶7 C.1∶2 D.2∶5

题目
某企业在软件园区的分公司有甲、乙2个开发团队。现从乙团队调走25人，此时甲、乙团队人数比为4∶3。然后又从甲团队调走42人，此时甲、乙团队人数之比2∶5。问两次调动之前，甲、乙团队人数比为：

A.3∶4
B.6∶7
C.1∶2
D.2∶5
相似考题

1.有甲、乙两个项目组。乙组任务临时加重时，从甲组抽调了四分之一的组员。此后甲组任务也有所加重，于是又从乙组调回了重组后乙组人数的十分之一。此时甲组与乙组人数相等。由此可以得出结论（ ）。A. 甲组原有16人，乙组原有11人 B. 甲、乙两组原组员人数之比为16∶11C. 甲组原有11人，乙组原有16人 D. 甲、乙两组原组员人数比为11∶16

2.甲、乙两物体都作匀速直线运动，已知甲、乙两物体运动时间之比4：5，通过的路程之比为3：2，则甲、乙两物体运动速度之比为（ ）A．6：5B．15：8C．5：6D．8：15

3.某厂有甲、乙、丙、丁四个车间，甲、乙两车间人数之比是9∶8,乙车间人数的5倍等于丙车间人数的4倍，丙车间人数的 等于丁车间人数的 ，如果丁车间工人数的8%退休以后还剩690人，那么甲车间有多少人?( )A.900 B.860 C.720 D.640

4.甲、乙两人有一定数量的苹果，若甲给乙39个苹果后两人苹果数量之比为5：7；若甲给乙44个苹果后两人苹果数量之比为3：5。问甲、乙共有多少个苹果? A．132 B．104 C．120 D．124

参考答案和解析
答案：B
解析：
第一步，本题考查基础应用题。
第二步，设第一次调动后甲团队的人数为4x，则乙的人数为3x，根据第二次调动可得（4x－42）∶3x＝2∶5，解得x＝15。
第三步，在两次调动前，甲团队的人数是4×15＝60（人），乙团队的人数是3×15＋25＝70（人），故甲、乙两队人数之比为6∶7。
更多“某企业在软件园区的分公司有甲、乙2个开发团队。现从乙团队调走25人，此时甲、乙团队人数比为4∶3。然后又从甲团队调走42人，此时甲、乙团队人数之比2∶5。问两次调动之前，甲、乙团队人数比为：”相关问题

  • 第1题：

    甲、乙两单位共同举办新年文艺联欢会，设一、二等奖若干。已知，甲、乙两单位获奖人数的比为4∶3；甲、乙两单位获一等奖的人数之和占两单位获奖人数总和的40%。甲、乙两单位获一等奖的人数之比为3∶4，甲单位获一等奖的人数占该单位获奖总人数的

    A.50%

    B.45%

    C.40%

    D.30%


    正确答案：D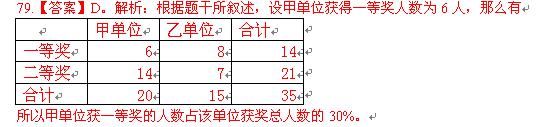

  • 第2题：

    有甲、乙两个项目组。乙组任务临时加重时，从甲组抽调了甲组四分之一的组员。此后甲组任务也有所加重，于是又从乙组调回了重组后乙组人数的十分之一。此时甲组与乙组人数相等。由此可以得出结论（ ）。

    A．甲组原有16人，乙组原有11人

    B．甲、乙两组原组员人数之比为16：11

    C．甲组原有11人，乙组原有16人

    D．甲、乙两组原组员人数之比为ll：16


    正确答案：B

    由题意可设甲组原有a人，乙组原有b人，则有(b+a/4)×9/10=1/10(b+a/4)+3a/4所以a：b=16：11，故本题选B。

  • 第3题：

    某公司将销售部门拆分为线上和线下两个团队，拆分后线上团队的人数为线下团队的2倍，线下团队男女员工人数相同，线上团队的男员工人数占两个团队男员工总数的60%，则拆分前，销售部门男女员工人数之比为：

    A.1∶2
    B.2∶3
    C.3∶5
    D.5∶7

    答案：D
    解析：
    第一步，本题考查基础应用题，用赋值法解题。
    第二步，赋值线下男员工为2个人，则线下女员工数也为2个人（如下表所示）。那么线下团队为4个人，则线上团队为8个人。线上团队的男员工人数占两个团队男员工总数的60%，因此线下男员工占两个团队的40%，男员工总数为2÷40%＝5，则线上男员工人数为5－2＝3（人），线上女员工为8－3＝5（人）。因此拆分前，男员工有5人，女员工有5＋2＝7（人）。男女比例为5∶7。

  • 第4题：

    甲、乙两车间原有人数的比为4：3，甲车间调12人到乙车间后，甲、乙两车间的人数变为2：3，甲车间原有人数是（　　）．

    A.18人
    B.35人
    C.40人
    D.144人

    答案：C
    解析：


    以甲车间原有40人.
    另解，甲、乙两车间原来人数之比为4：3=20：15，调整后人数之比为2：3=14：21，可知甲车间减少了20-14=6份=12人，每份2人，则甲车间原有20×2=40人.

  • 第5题：

    某单位有甲、乙两个部门，若从甲部门调动7个人到乙部门，则乙部门的人数比甲部门的 人数多2倍，若从乙部门调动5个人到甲部门，则甲、乙两部门人数相等，问甲部门有多少 人？（ ）

    A. 12
    B. 15
    C. 17
    D. 19

    答案：D
    解析：

  • 第6题：

    某公司有甲、乙两个销售团队，共50人，其中女性员工有18人。甲团队男女比例为5：3，乙团队男女比例为2：1，那么，乙团队的男性员工共有（　　）名。

    A.18
    B.20
    C.12
    D.9

    答案：C
    解析：

  • 第7题：

    企业向甲、乙、丙三个优秀研发团队发放总额为X万元的奖金。如只发给甲团队，平均每人能得到20万元；如只发给乙团队，平均每人能得到24万元；如只发给丙团队，平均每人能得到30万元。现企业决定向甲团队每人发放2万元，剩余奖金平均分配给乙、丙两个团队的每个人。问乙团队的每名成员得到多少万元的奖金？（ ）

    A.10
    B.11
    C.12
    D.13

    答案：C
    解析：
    本题属于约数倍数问题。
    由题意知X为20、24、30的公倍数，赋值X为120，则甲团队人数为120/20=6，乙团队人数为120/24=5，丙团队人数为120/30=4。向甲团队每人发放2万元，剩余奖金为120-2×6=108,剩余奖金平均分配给乙、丙两个团队的每个人，乙、丙团队的每名成员得到108÷（5+4）=12万元。A、B、D选项错误。
    因此，选择C选项。

  • 第8题：

    甲、乙两个学校的在校生人数之比为5：3，甲学校如果转入30名学生，再将85名学生转到乙学校，则两个学校在校生人数相同。则此时乙学校学生人数在以下哪个范围内 《》（ ）

    A.不到200人
    B.在200～240人之间
    C.在241～280人之间
    D.超过280人

    答案：C
    解析：

  • 第9题：

    有甲、乙两个课外活动小组，甲组的人数是乙组的4/5，后来又从乙组调16人到甲组，这时乙组人数是甲组的3/4，甲、乙两组原来各有多少人？（ ）
    A.甲组40人，乙组50人 B.甲组80人，乙组100人
    C.甲组48人，乙组60人 D.甲组56人，乙组70人


    答案：D
    解析：

  • 第10题：

    单选题
    甲、乙、丙三个旅行团的游客人数都相等，且每个游客的平均年龄都是32岁，这三个团游客年龄的方差分别是S甲2＝27，S乙2＝19.6，S丙2＝1.6．导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选（　　）．
    A

    甲团

    B

    乙团

    C

    丙团

    D

    甲团或乙团


    正确答案： D
    解析：
    三组数据中，丙团游客年龄的方差最小，表明丙团游客年龄的波动最小，年龄最接近．

  • 第11题：

    单选题
    用甲人群作为标准，对乙人群进行标化，标准化死亡比的计算公式是（）
    A

    乙人群实际死亡数／甲人群死亡专率×乙人群的观察人数

    B

    乙人群实际死亡数×甲人群死亡专率／乙人群的观察人数

    C

    甲人群死亡专率×乙人群的观察人数／乙人群实际死亡数

    D

    乙人群实际死亡数／甲人群预期人数

    E

    甲人群预期死亡数／乙人群实际死亡数


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    某企业在软件园区的分公司有甲、乙2个开发团队，现从乙团队调走25人，此时甲、乙团队人数比为4:3，然后又从甲团队调走42人，此时甲、乙团队人数比为2:5。问两次调动之前，甲、乙团队人数比为：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： B
    解析：

  • 第13题：

    某公司l00名员工对甲、乙两名经理进行满意度评议，对甲满意的人数占全体参加评议员工的3/5，对乙满意的人数比甲的人数多6人，对甲、乙都不满意的占都满意人数的1/3多2人，则对甲、乙都满意的人数是多少人？

    A．36

    B．26

    C．48

    D．42


    正确答案：D

  • 第14题：

    甲乙丙三箱水果，甲与乙的重量之比为3：4，甲与丙的重量之比为5：2，从乙箱取4千克放入丙箱，乙丙重量之比为9：4，则甲、乙、丙三箱重量之和为多少千克? A．40 B．82 C．80 D．70


    正确答案：B
    由题意可知，甲：乙：丙=15：20：6，乙、丙重量比为20：6=10：3。乙丙一共有10+3=13份．置换后重量之比为9：4，依旧是13份。因此乙减少的一份为4千克。所以乙、丙共有13x4=52千克，甲有52÷(20+6)×15=30千克。故共有52+30=82千克。

  • 第15题：

    某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8，分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3，乙科室为5∶2。则丙科室男女员工人数之比为：

    A.1∶2
    B.2∶3
    C.5∶9
    D.5∶8

    答案：C
    解析：
    第一步，本题考查基础应用题，用赋值法解题。
    第二步，根据男女比为15∶13，则总人数应该为28的倍数；又因为甲∶乙∶丙＝5∶7∶8，则总人数应该为20的倍数；所以赋值总人数为140，则男生人数为75，女生人数为65。甲＝35，乙＝49，丙＝56。又因为甲科室的男女比为4∶3，则甲的男生为20，甲的女生为15，又因为乙科室的男女比为5∶2，则乙的男生为35，乙的女生为14，所以得出丙的男生为75－20－35＝20，丙的女生为65－15－14＝36，则丙的男女比＝20∶36＝5∶9。

  • 第16题：

    甲、乙两个单位分别有60和42名职工，共同成立A、B两个业余活动小组，所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%，乙单位职工中参加B组的人数与参加A组的人数之比为3∶4，参加B组的人中，甲单位职工占5/8。问有多少人仅参加A组?

    A.35
    B.42
    C.46
    D.56

    答案：C
    解析：
    第一步，本题考查容斥问题。
    第二步，设乙单位只参加一个小组的人数为5x，则只参加A组的有5x·60%=3x名职工，那么只参加B组的有5x－3x=2x名职工，设乙单位AB组都参加的有y人。可列方程：（2x＋y）∶（3x＋y）＝3∶4，解得x＝y，那么乙单位中参加B组的有3x人，参加A组的有4x人，AB都参加的有x人，可列方程：3x＋4x－x＝42，解得x＝7，那么参加B组的有21人，只参加A组的有21人。

    那么甲单位只参加A组的有60－35＝25（人），那么两个单位只参加A组的有21＋25＝46（人）。

  • 第17题：

    某单位有甲和乙两个人数相同的处室，甲处室党员人数是群众人数的1.5倍，而两个处室党员总人数与群众总人数正好相同。现从甲处室调走10名党员后，甲处室和乙处室党员占各自处室现有职工的比例相同。则两个处室最初共有多少人？

    A.48
    B.60
    C.72
    D.90

    答案：B
    解析：
    第一步，本题考查方程问题。第二步，甲乙两个处室人数相同，甲党员和群众人数之比为3:2，所以乙党员和群众人数之比 为2:3，设甲党员和群众人数分别为3x和2x,所以（3x-10）：2x＝2:3，可得，x=6，所以总人数为2×5x＝10x＝60。因此，选择B选项。

  • 第18题：

    统计图：根据下面的统计图。回答它后面的5道题目。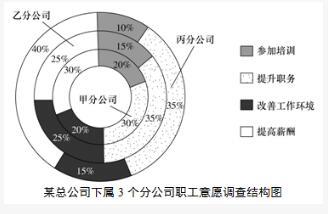

    假设甲、乙、丙3个分公司的职工人数相同，总公司某年度计划对3个分公司中有意愿提升职务的职工进行职务提升，晋升比例为每5位有意愿的职工中提升1位，那么：

    A.甲分公司获得职务提升的职工人数不一定比乙、丙的少
    B.乙分公司获得职务提升的职工人数不可能多于甲分公司
    C.甲、乙、丙3个分公司获得职务提升的职工人数之和将超过甲分公司职工总人数
    D.乙、丙分公司获得职务提升的职工人数不一定相同

    答案：A
    解析：
    第一步，本题考查综合分析问题，且需选出正确的一项。
    第二步，A选项，读数比较。定位饼图，虽然甲分公司有意愿提升职务的职工占比（30%）小于乙、丙两分公司的占比（均为35%），但晋升比例为每5位有意愿的职工中提升1位，所以要是有意愿的职工人数之差不到5位，那么获得职务提升的职工人数就相等，满足的条件是各分公司人数小于100人，正确。
    B选项，部分量比较。定位饼图，当每个分公司都是100人时，乙分公司获得职务提升的职工人数=35÷5=7（人），就会多于甲分公司30÷5=6（人），错误。
    C选项，比重比较。定位饼图，甲、乙、丙3个分公司有职务提升意愿的职工人数占比之和为30%＋35%＋35%＝1，晋升人数占比为1÷5＝20%，所以获得职务提升的职工人数之和不可能超过甲分公司职工总人数1，错误。
    D选项，读数比较。定位饼图，由于乙、丙分公司的公司人数相等，有意愿提升职务的职工占比也相等，所以获得职务提升的职工人数一定相同，错误。
    因此，选择A选项。

  • 第19题：

    某部门有甲、乙、丙、丁四个团队，甲、乙两个团队共有78人，乙、丙两个团队共有86人，甲、丁两个团队共有80人，请问，丙、丁两团队共有多少人?（　　）

    A.98
    B.96
    C.88
    D.86

    答案：C
    解析：
    乙丙+甲丁=86+80，甲乙=78人，所以丙丁=86+80-78=88(人)。

  • 第20题：

    某公司有甲、乙、丙、丁四个事业部，甲和丁事业部人数之和是乙和丙人数之和的2倍，甲事业部人数是乙的5倍，丙事业部人数是丁的3倍。问丁事业部人数相当于四个事业部总人数的：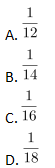


    答案：B
    解析：
    解法一：
    第一步，本题考查基础应用题，用方程法解题。
    第二步，设丁事业部的人数为x人，则丙事业部人数为3x人。设乙事业部人数为y人，则甲事业部人数为5y人。根据“甲和丁事业部人数之和是乙和丙人数之和的2倍”可列式：5y＋x＝2×（y＋3x），化简得3y＝5x，因此四个事业部总人数为5y＋y＋3x＋x＝6y＋4x＝14x，则丁事业部人数相当于四个事业部总人数的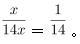
    因此，选择B选项。
    解法二：
    第一步，本题考查基础应用题，用赋值法解题。
    第二步，赋值丁事业部的人数为1人，则丙事业部的人数为3人。根据“甲和丁事业部人数之和是乙和丙人数之和的2倍”，可得到：甲＋1＝2×（乙＋3），又因为甲是乙的5倍，因此可以求得乙为，甲为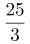。总人数＝1＋3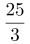＋＋＝14，因此丁占总人数的。
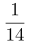    因此，选择B选项。

  • 第21题：

    某俱乐部男、女会员的人数比是3:2，分为甲、乙、丙三组。巳知甲、乙、丙三组的人数比是10:8:7，甲组中男、女会员的人数之比是3:1，乙组中男、女会员的人数之比是5:3。求丙组中男、 女会员的人数之比？


    A.l:2
    B.3:5
    C.4:7
    D.5:9

    答案：D
    解析：
    根据题中的比例关系，列表如下：因为甲组男女比例为3:1,则甲的总人数应为4的倍数，设各部分人数比为20:16:14，根据各部分比例关系， 列男女人数到表格，进而算得丙组中男、女会员的人数之比为5:9。

  • 第22题：

    单选题
    某企业在软件园区的分公司有甲、乙两个开发团队，先从乙团队调走25人，此时甲、乙团队人数比为4:3，然后又从甲团队调走42人，此时甲、乙团队人数比为2：5，则两次调动前甲、乙团队人数比为：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： A
    解析：

  • 第23题：

    单选题
    某企业在软件园区的分公司有甲、乙两个开发团队，先从乙团队调走25人，此时甲、乙团队人数比为4:3.然后又从甲团队调走42人，此时甲、乙团队人数比为2:5，则两次调动前甲、乙团队人数比力：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： B
    解析：

相关内容