如图所示，梯形ABCD的底边上有两个球M、N分别从A、B两点相向滚动，分别到达B、A两点之后保持静止。已知球N的速度是M的3倍，问下列能正确反映BDN构成的三角形面积与ACM构成的三角形面积之比随球M位移变化的图像是（横轴为位移，纵轴为面积之比）：

题目
如图所示，梯形ABCD的底边上有两个球M、N分别从A、B两点相向滚动，分别到达B、A两点之后保持静止。已知球N的速度是M的3倍，问下列能正确反映BDN构成的三角形面积与ACM构成的三角形面积之比随球M位移变化的图像是（横轴为位移，纵轴为面积之比）：



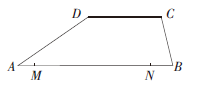
相似考题

1.在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线,求证:M与N分别是AC和CD的中点。

2.将一块三角形绿地沿一条直线分成两个区域，一为三角形，一为梯形，已知分出的三角行区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩？A．9.6 B．11.2 C．10.8 D．12.0

3.将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角行区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩？ （ ）A．9.6B．11.2C．10.8D．12.0

4.将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩?（ ）A．9.6B．11.2C．10.8D．12.0

参考答案和解析
答案：C
解析：
设M前进的速度为v，则N的速度为3v，梯形ABCD的高为h（固定不变）。在N到达点A之前，BN=3AM，且两个三角形的高均为h，所以S△BDN∶S△ACM=3，保持不变；当N到达点A后，S△BDN=(1/2) AB h=C（定值），面积保持不变，S△ACM=(1/2) AM h，故S△BDN∶S△ACM=C∶[(1/2) AM h]=2C/(AM h)，C和h都是定值，S△BDN与S△ACM之比是反比函数曲线；当点M到达点B，S△BDN=S△ACM，即S△BDN∶S△ACM=1。故本题选C。
更多“如图所示，梯形ABCD的底边上有两个球M、N分别从A、B两点相向滚动，分别到达B、A两点之后保持静止。已知球N的速度是M的3倍，问下列能正确反映BDN构成的三角形面积与ACM构成的三角形面积之比随球M位移变化的图像是（横轴为位移，纵轴为面积之比）： ”相关问题

  • 第1题：

    一质量为5 kg的物体在恒力F作用下，从静止开始做匀加速直线运动。已知第5 s内的位移为9 m，则此物体前4 s内的位移为__________m，此恒力的大小F=__________N。


    答案：
    解析：
    16,10

  • 第2题：

    如图，在梯形ABCD中，AB//CD，O为AC与BD的交点，CO=2AO，则梯形ABCD与三角形AOB的面积之比为：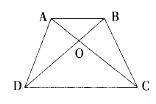


    A.6：1
    B.7：1
    C.8：1
    D.9：1

    答案：D
    解析：
    在梯形中，上底与下底平行，可得△AOB~△COD，其面积之比等于对应边AO、CO之比的平方，为1:4。△AOB与△BOC可看成两个等高的三角形，面积之比等于底AO、CO之比，为1:2。显然△AOD与△BOC面积相等。设△AOB面积为1，则梯形面积为1+2+2+4=9。故所求为9:1。

  • 第3题：

    如图所示，在xOy平面内有一列简谐横波沿x轴正方向传播，M、N为传播方向上的两点，在t=0时M点位于平衡位置，且运动方向向上，N点位于平衡位置上方的最大位移处。则下列说法正确的是(波长为A，k=0，1，2，3，…)( )。


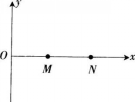    A．MN两点间距离为(k+1/4)λ
    B．MN两点间距离为(k+1/2)λ
    C．MN两点间距离为(k+3/4)λ
    D．MN两点间距离为(k+1)A

    答案：C
    解析：
    t=0时M点位于平衡位置，且速度方向向上，N点位于平衡位置上方的最大位移处，则MN问最短有3/4个波长的波形，则MN两点间距离为(k+3/4)λ，(k=0，1，2，…)，故C正确。

  • 第4题：

    某套二手住宅，套内建筑面积下的价格为2000元/m2，套内建筑面积与本套住宅建筑面积之比为0.92，使用面积与建筑面积之比为0.8，则本套住宅建筑面积下的价格为( )元/m2。

    A.1600
    B.1840
    C.2000
    D.2174

    答案：B
    解析：

  • 第5题：

    以如下图的圆形广场上举办一个市民文艺活动，参加活动的n名市民排成如图中的ABCD的菱形方阵（图中数字单位为米）。已知方阵面积为m平方米，且n=2m，问n的值为：



    A.92
    B.120
    C.192
    D.240

    答案：C
    解析：

  • 第6题：

    计算题：已知三角形的三条边分别为7m、8m、9m，求该三角形面积？


    正确答案: 根据公式：S=√L（L-a）（L-b）（L-c），L=（a＋b＋c）/2
    已知L=（7+8+9）/2=12（m）
    ∴三角形面积S=√L（L-a）（l-b）（l-c）=√12（12-7）（12-8）（12-9）=26.83（m2）

  • 第7题：

    喷射泵的喉嘴面积比m是指（）。

    • A、喷嘴出口面积与混合室进口截面积之比
    • B、混合室进口截面积与喷嘴出口面积之比
    • C、喷嘴出口面积与圆柱段截面积之比
    • D、圆柱段截面积与喷嘴出口面积之比

    正确答案:D

  • 第8题：

    面积置换率m是指：复合地基中（）所占面积与（）所占面积之比。


    正确答案:桩体；桩土总面积

  • 第9题：

    比收尘面积是单位流量的烟气所分配到的集尘面积，它等于集尘面积与烟气流量之比，单位为（）。

    • A、m2／s；
    • B、m2／（m3•s－1）；
    • C、s／m2；
    • D、m2／（m2•s－1）。

    正确答案:B

  • 第10题：

    问答题
    计算题：已知三角形的三条边分别为7m、8m、9m，求该三角形面积？

    正确答案： 根据公式：S=√L（L-a）（L-b）（L-c），L=（a＋b＋c）/2
    已知L=（7+8+9）/2=12（m）
    ∴三角形面积S=√L（L-a）（l-b）（l-c）=√12（12-7）（12-8）（12-9）=26.83（m2）
    解析： 暂无解析

  • 第11题：

    单选题
    两颗直径不同的玻璃球分别在水中和空气中以相同的速度自由沉降。已知玻璃球的密度为2500kg/m3，水的密度为998.2kg/m3，水的粘度为1.005×10-3Pas，空气的密度为1.205kg/m3，空气的粘度为1.81×10-5Pas。若在层流区离心沉降，已知旋风分离因数与旋液分离因数之比为2，则水中颗粒直径与空气中颗粒直径之比为（）。
    A

    10.593

    B

    11.593

    C

    12.593

    D

    13.593


    正确答案： A
    解析： 暂无解析

  • 第12题：

    问答题
    有一个面积为0.8m三角形铁板，底边0.4m，求该三角形的高为多少米？

    正确答案： SΔ=1/2*（a·h）
    ∴h=2SΔ／a=2*0.8／0.4=4（m）
    三角形铁板的高为4米.
    解析： 暂无解析

  • 第13题：

    如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是


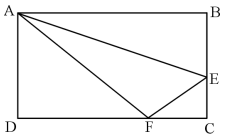    A.5∶1
    B.5∶2
    C.5∶3
    D.2∶1

    答案：A
    解析：
    第一步，三角形ABE、三角形ADF与四边形AECF的面积相等，则三者各占长方形ABCD面积的1/3。连接辅助线AC，则三角形ACD的面积为长方形的1/2。?



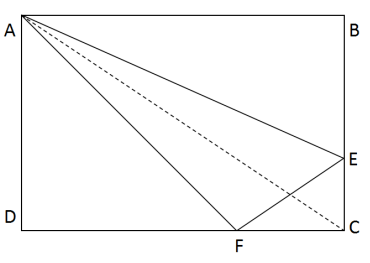
    第二步，三角形ADF与三角形ACD的高相同，都为AD，三角形高相同，底边之比等于面积之比，则FD：CD＝2：3，所以CF＝1/3CD，同理CE＝1/3BC，因此三角形CEF的面积为长方形面积的1/18，则三角形AEF的面积为长方形面积的1/3－1/18＝5/18，所以两者面积之比为5：1。解法二：赋值长方形的长为6，宽为3，则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等，则三者的面积各为6。那么FD的长为4，CF长2，则CE的长为1，则三角形CEF的面积为1，三角AEF的面积为6－1＝5，则两者的面积之比为5：1。因此，选择A选项。

  • 第14题：

    如图所示，真空中有A、B两个等量异种点电荷，0、M、N是AB连线的垂线上的三个点，且A O>OB。一个带负电的检验电荷仅在电场力的作用下，从M点运动到N点，其轨迹如图中实线所示。若M、N两点的电势分别为M和N，检验电荷通过M、Ⅳ两点的动能分别为Ekm和Ekn，则( )。


    答案：B
    解析：
    由于带负电的检验电荷仅在电场力的作用下由M运动到Ⅳ，说明检验电荷受到的电场力方向大致是向左的，故A带正电，B带负电，又因为AO>OB，所以M、Ⅳ两点的电势并不相等，M处于更接近B点的等势面上，N处于更远离B点的等势面上，故φM＜φN。由于检验电荷带负电，故带负电的检验电荷处于N点时的电势能小于在M点时的电势能．故在Ⅳ点时的动能大于在M点时的动能，即EKM＜EKN，B项是正确的。

  • 第15题：

    如图所示，一个内表面光滑的半球型碗放在水平桌面上，碗口处于水平状态，0是球心，有两个带同种电荷的质量分别为m1和m2的视为质点的小球，当它们静止后处于如图所示的状态，则m1和m2两球对碗的弹力大小之比为（　　）。




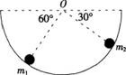    答案：B
    解析：

  • 第16题：

    如图所示，梯形ABC.D的底边上有两个球M、N分别从A、B两点相向滚动，分别到达B、A两点之后保持静止。已知球N的速度是M的3倍，问下列能正确反映BDN构成的三角形面积与AC.M构成的三角形面积之比随球M位移变化的图像是（横轴为位移，纵轴为面积之比）：




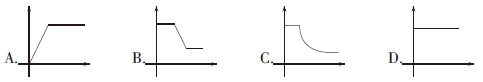    答案：C
    解析：
    设M前进的速度为v，则N的速度为3v，梯形ABCD的高为h（固定不变）。在N到达点A之前，BN=3AM，且两个三角形的高均为h，所以S△BDN∶S△ACM=3，保持不变；当N到达点A后，S△BDN=(1/2)?AB?h=C（定值），面积保持不变，S△ACM=(1/2)?AM?h，故S△BDN∶S△ACM=C∶[(1/2)?AM?h]=2C/(AM?h)，C和h都是定值，S△BDN与S△ACM之比是反比函数曲线；当点M到达点B，S△BDN=S△ACM，即S△BDN∶S△ACM=1。故本题选C。

  • 第17题：

    有一个面积为0.8m三角形铁板，底边0.4m，求该三角形的高为多少米？


    正确答案: SΔ=1/2*（a·h）
    ∴h=2SΔ／a=2*0.8／0.4=4（m）
    三角形铁板的高为4米.

  • 第18题：

    已知M、N两点间的高差为4m，两点的实际水平距离为800m，则M、N两点间的坡度为（）。

    • A、5%
    • B、5‰
    • C、50%
    • D、50‰

    正确答案:B

  • 第19题：

    如图所示的是北半球的一段纬线，M、N分别是X日的晨线、昏线与该纬线的交点。X日M、N两点的经度差为90°，一年中M、N两点有重合于O点的现象。读图回答下列小题。 X日M地的昼长为（）

    • A、6小时
    • B、9小时
    • C、12小时
    • D、18小时

    正确答案:A

  • 第20题：

    球面度是一立体角，其顶点位于球心面，它在球面上所截取的面积等于（）的面积。

    • A、以球的半径为边长的正方形
    • B、以球的半径为边长的等边三角形
    • C、以球直径为边长的正方形
    • D、以球直径为边长的等边三角形

    正确答案:A

  • 第21题：

    单选题
    喷射泵的喉嘴面积比m是指（）。
    A

    喷嘴出口面积与混合室进口截面积之比

    B

    混合室进口截面积与喷嘴出口面积之比

    C

    喷嘴出口面积与圆柱段截面积之比

    D

    圆柱段截面积与喷嘴出口截面积之比


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    一只盒子中有红球m个，白球10个，黑球n个，每个球除颜色外其他都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是（　　）．
    A

    m＝4，n＝6

    B

    m＝5，n＝5

    C

    m＋n＝5

    D

    m＋n＝10


    正确答案： B
    解析：
    因为从中任取一个球，取得白球的概率与不是白球的概率相同．所以白球的个数与不是白球的球的个数相等，所以m＋n＝10．

  • 第23题：

    单选题
    球面度是一立体角，其顶点位于球心面，它在球面上所截取的面积等于（）的面积。
    A

    以球的半径为边长的正方形

    B

    以球的半径为边长的等边三角形

    C

    以球直径为边长的正方形

    D

    以球直径为边长的等边三角形


    正确答案： C
    解析： 暂无解析

相关内容