一个等差数列有2n—1项，所有偶数项的和为40，所有奇数项的和为50，那么该数列共有( )项。 A. 7 B. 8 C. 9 D. 10

题目
一个等差数列有2n—1项，所有偶数项的和为40，所有奇数项的和为50，那么该数列共有( )项。

A. 7
B. 8
C. 9
D. 10
相似考题

1.已知一个等差数列的首项为1，公差为3，那么该数列的前5项和为 （ ）A.35B.30C.20D.10

2.已知公差为2的正整数等差数列为an，则该数列满足不等式7/16＜an/5＜398/9的所有项的和为（ ）A．12320B．12430C．12432D．12543

3.一个等差数列，它的开始四项之和为70，最后四项之和为10，所有项的和为640，则这个数列一共有（ ）项。A、 56B、 60C、 64D、 72

4. 一个等差数列，它的开始四项之和为70，最后四项之和为10，所有项的和为640，则这个数列一共有(　)项。A、 56　　B、 60　　C、 64　　D、 72

更多“一个等差数列有2n—1项，所有偶数项的和为40，所有奇数项的和为50，那么该数列共有( )项。 ”相关问题

  • 第1题：

    设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。


    正确答案：
    15

  • 第2题：

    有一个30项的等差数列，和为3675，它的每一项都是正整数，那么其中最大的一项的最大值是多少？( )

    A.137
    B.166
    C.224
    D.244

    答案：C
    解析：
    由等差数列求和公式可知(首项+末项)×30÷2=3675，可得首项+末项=245，设该等差数列的首项为a，公差为d(a、d均为正整数)，则有2a+29d=245，2a为偶数，而245为奇数，则29d为奇数，要使最大的项最大，即使d最大，245÷29=8……13，所以d最大为7，此时a=(245-29×7)÷2=21，最大的项为245-21=224。

  • 第3题：

    已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）

    A.3
    B.1
    C.-1
    D.-3

    答案：A
    解析：

  • 第4题：

    等差数列前n项和为210,其中前4项和为40,后4项的和为80,则n的值为（ ）

    A.10
    B.12
    C.14
    D.16
    E.18

    答案：C
    解析：

  • 第5题：

    已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）

    A.248
    B.168
    C.128
    D.19
    E.以上选项均不正确

    答案：B
    解析：

  • 第6题：

    —个等差数列有2n —1项，所有偶数项的和为40,所有奇数项的和为50，那么该数列共有 ( )项。

    A. 7 B. 8 C. 9 D. 10


    答案：C
    解析：

  • 第7题：

    案例：

    在等差数列的习题课教学中，教师布置了这样一个问题：等差数列前10项和为100，前100项和为10，求前110项的和。

    两位学生的解法如下：

    学生甲：设等差数列的首项为a1，公差为d，则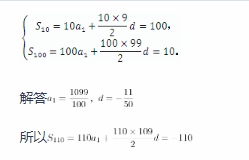

    学生乙：设等差数列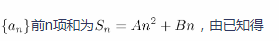


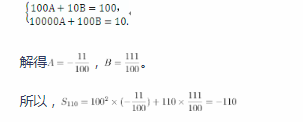
    针对上述解法，一些学生提出了自己的想法。

    （1）请分析学生甲和学生乙解法各自的特点，并解释学生乙设的理由。（12分）

    （2）请验证(*)中结论是否成立。


    答案：
    解析：
    本题主要从“等差数列”相关知识入手，考查等差数列的相关概念、等差数列的通项公式、求和公式等基层知识，教学工作的基本环节，常用的教学方法，以及课堂导入技巧等基本知识与技能。

  • 第8题：

    联项和量项被称为下面哪一个？（）

    • A、数项
    • B、常项
    • C、变项
    • D、量项

    正确答案:B

  • 第9题：

    从无数项具体的个别的政策抽象出所有的政策的共同本质和属性，这就是（）

    • A、政策群
    • B、政策链
    • C、政策一般
    • D、政策系统

    正确答案:C

  • 第10题：

    汇编语言源程序中，每个语句由四项组成，如语句要完成一定功能，那么该语句中不可省略的项是（）。 

    • A、名字项
    • B、操作项
    • C、操作数项
    • D、注释项

    正确答案:B

  • 第11题：

    我国实行土地公有制，我国土地制度的主要特点为（），土地所有者将其所有权四项职能中的一项或数项让与土地使用者，土地使用者由此获得土地使用权或空间权、地役权。

    • A、集体所有
    • B、不可交易性
    • C、所有权与使用权相分离
    • D、所有权与使用权相结合

    正确答案:C

  • 第12题：

    单选题
    “斐波那契数列”可以拆分成：（）。
    A

    两个等比数列

    B

    两个等差数列

    C

    一个等差数列和一个等比数列

    D

    无法拆分


    正确答案： A
    解析： 暂无解析

  • 第13题：

    已知公差为2的正整数等差数列为an ，则该数列满足不等式7/16 ＜an/5 ＜398/9 的所有项的和为（ ）

    A. 12320
    B. 12430
    C. 12432
    D. 12543

    答案：A
    解析：
    公差为2的正整数数列为奇数列，满足条件的an 最小为3，最大为221，故和为(3+22)*[(221-3)/2+1]/2=12320 。故答案为A。

  • 第14题：

    已知等差数列前n项和
    (Ⅰ)求这个数列的逋项公式；
    (II)求数列第六项到第十项的和．


    答案：
    解析：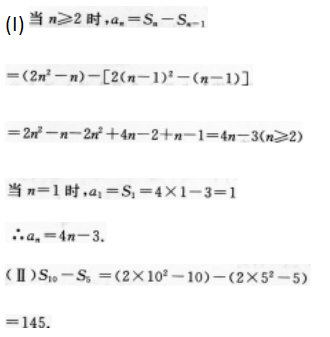

  • 第15题：

    一个无穷等比数列所有奇数项之和为45,所有偶数项之和为-30,则其首项等于（ ）

    A.24
    B.25
    C.26
    D.27
    E.28

    答案：B
    解析：

  • 第16题：

    已知某等差数列共有20项,其奇数项之和为30,偶数项之和为40,则其公差为（ ）.

    A.5
    B.4
    C.3
    D.2
    E.1

    答案：E
    解析：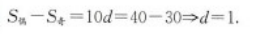

  • 第17题：

    一个等差数列的前12项的和为354,前12项中偶数项之和与奇数项之和的比是32:27,则其项数为（ ）

    A.3
    B.4
    C.5
    D.6
    E.7

    答案：C
    解析：

  • 第18题：

    案例：

    在等差数列的习题课教学中，教师布置了这样一个问题：等差数列前10项和为100，前100项和为10，求前110项的和。

    两位学生的解法如下：

    学生甲：设等差数列的首项为a1，公差为d，则


    针对上述解法，一些学生提出了自己的想法。

    （1）请分析学生甲和学生乙解法各自的特点，并解释学生乙设的理由。（12分）

    （2）请验证(*)中结论是否成立。（8分）


    答案：
    解析：

  • 第19题：

    一个等差数列首项为32，该数列从第15项开始小于1，则此数列的公差d的取值范围是()．?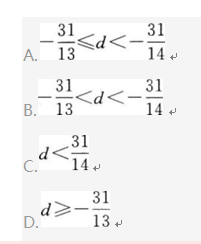


    答案：A
    解析：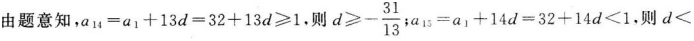

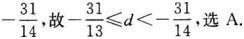
  • 第20题：

    用半数平均法修匀时间数列时，如果所给时间数列为奇数项，则可把时间数列的第一项删去。


    正确答案:正确

  • 第21题：

    间接平差时，一测站所有方向误差方程式中的常数项之代数和为（）。


    正确答案:0

  • 第22题：

    一个等差数列共有2N+1项，所有奇数项的和为64，所有偶数项的和为56，那么N的值为（）

    • A、5
    • B、6
    • C、8
    • D、7

    正确答案:D

  • 第23题：

    填空题
    间接平差时，一测站所有方向误差方程式中的常数项之代数和为（）。

    正确答案： 0
    解析： 暂无解析

相关内容