五（1）班有25人，许多同学参加了课外小组。参加音乐组的有12人，参加美术组的有10人，两个组都没参加的有6人。既参加音乐组又参加美术组的有多少人？
题目
五（1）班有25人，许多同学参加了课外小组。参加音乐组的有12人，参加美术组的有10人，两个组都没参加的有6人。既参加音乐组又参加美术组的有多少人？
相似考题
更多“五（1）班有25人，许多同学参加了课外小组。参加音乐组的有12人，参加美术组的有10人，两个组都没参加的有6人。既参加音乐组又参加美术组的有多少人？”相关问题
-
第1题：
某班有35个学生．每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组（ ）
A．15人
B．16人
C．17人
D．18人
正确答案：A
设选两门课的人数为A，有(13+17+30)-A-2×5=35，得A=15。所以只报一门的人数为35-15-5=15。 -
第2题：
某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组 都参加．那么有多少人两个小组都不参加?（ ） A．16 B．17 C．18 D．19
正确答案：B
依据题意，只参加数学小组的同学有15—10=5人，只参加航模小组的同学有18－10＝8人，两个小组都参加的同学有10人，所以有40一23＝17人两个小组都不参加。故选B。
-
第3题：
某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有 人。
正确答案：
答案：8 -
第4题：
某班参加体育活动的学生有25 人，参加音乐活动的有26 人，参加美术活动的有24 人，同时参加体、音活动的有16 人，同时参加音、美活动的有15 入，同时参加美、体活动的有14 人，三个组织都参加的有5 人，这个班共有多少名学生参加活动？（ ）。A.24
B.26
C.30
D.35答案：D解析：由三个集合的容斥原理可以得到，这个班参加活动的学生有
25+26+24-16-15-14+5=35 人。 -
第5题：
某班参加体育活动的学生有25人，参加音乐活动的有26人，参加美术活动的有24人，同时参加体、音活动的有16人，同时参加音、美活动的有15人，同时参加美、体活动的有14人，三个组织都参加的有5人，这个班共有多少名学生参加活动?（ ）A.24
B.26
C.30
D.35逛街答案：D解析：典型的三个集合的容斥问题，由三个集合的容斥原理可以得到，这个班参加活动的学生有25+26+24-16-15-14+5=35人。 -
第6题：
某部门组织一次活动，包括唱歌、聚餐和出游三个项目。其中，5人请病假没有参加任何活动，只参加1个项目的比没参加的人多，但不到10人，他们恰好可以平均分成3组：只参加2个项目的有十几个人，他们恰好可以平均分成4组；3个项目都参加的占到部门人数的一半，他们恰好可以平均分成5组。那么这个部门一共有多少人？( )A.30
B.40
C.60
D.80答案：C解析：依题意，只参加1个项目的有6或9人，只参加2个项目的有12或16人，没参加任何活动的有5人。因为3个项目全参加的占总人数的一半，且能被5整除，则只参加1个和2个项目的人数总和也应被5整除，只能是9+16=25，总人数为(25+5)×2=60。 -
第7题：
某班有36名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有（ ）A.6人
B.7人
C.8人
D.9人
E.10人答案：C解析：由条件知,每名同学至多参加两个小组,故不可能出现一名同学同时参加数学、物理、化学课外研究小组,设同时参加数学和化学小组的有x人,根据容斥原理有26+15+13-（6+4+x）=36,解得x=8.故同时参加数学和化学小组的有8人,应选C. -
第8题：
99-100题属于以下题干。
某单位工会成立职工业余兴趣活动小组，分台球、乒乓球、羽毛球、登山四个小组。已知该
单位的甲、乙、丙、丁、戊、己、庚等7人每人各参加其中的两个小组，每个小组最少有其中的两人参加。最多有其
中的5人参加。另外，还知道：
（1）丁与戊的参加情况完全相同；
（2）己与庚的参加情况完全相同；
（3）如果甲参加台球组，则丁也会参加台球组
（4）只有乙和丙参加乒乓球组
如果登山组只有己和庚参加，则可以得出以下哪项？A.甲参加台球组，羽毛球组
B.乙参加台球组，羽毛球组
C.己参加台球组，登山组
D.庚参加羽毛球组,登山组答案：A解析：因为兵乓组里面只有乙，丙，题中又说登山组只有己，庚，所以其他人只能去剩下的台球和羽毛球组，因
为一个人最多在两个组，所以可以排除B,C,D，只能选择A。 -
第9题：
某班56名学生参加了奥数或作文课外兴趣小组的活动，其中参加奥数的有32人，参加作文的有35人，问两种活动都参加的有多少人?()A. 3
B. 11
C. 21
D. 24答案：B解析：两种活动都参加得人有32+35-56=11人。故答案为B。 -
第10题：
某校四年级(1)班的全体学生参加课外兴趣小组活动。参加数学奥林匹克辅导的学生比全班人数的 一半还多2人，参加英文打字的学生比余下的一半还多4人，这时还剩下7名学生参加美术组活动。 四年级(1)班共有多少学生？（ ）
A. 30 B. 42 C. 48 D. 62答案：C解析：根据题中已知条件和所求问题，画线段图如下：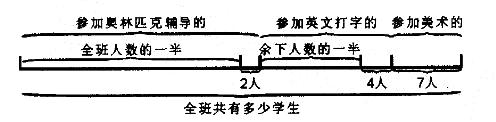
可以用倒推的方法进行思考：
(1)假如参加英文打字的人数正好是余下人数的一半而不多于4人，那么余下人数的一半是7 + 4 = 11（人）。由此可算出余下人数是11X2 = 22（人）。
(2)假如参加奥林匹克辅导的人数正好是全班人数的一半而不多于2人，那么全班人数的一半是22 + 2 = 24（人），由此可得全班人数是24X2 = 48（人）。 -
第11题：
某工厂有100名工人报名参加了4项专业技能课程中的一项或多项，已知A课程与B课程不能同时报名。如果按照报名参加的课程对工人进行分组，将报名参加的课程完全一样的工人分到同一组中，则人数最多的组最少有多少人?
- A、7
- B、8
- C、9
- D、10
正确答案:D -
第12题：
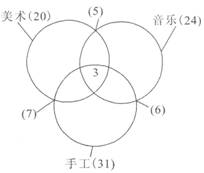
某年级的课外小组分为美术、音乐、手工三个小组，参加美术小组有20人，参加音乐小组有24人，参加手工小组有31人，同时参加美术和音乐两个小组有5人，同时参加音乐和手工两个小组有6人，同时参加美术和手工两个小组的有7人，三个小组都参加的有3人，这个年级参加课外小组的同学共有多少人?（ ） A．75人 B．57人 C．63人 D． 60人
正确答案：D
如图所示，由容斥原理可知，这个年级参加课外小组的有20+24+31－(5+6+7)+3＝60人。故选D。
-
第13题：
两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古 文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。 下列是上述论证依赖的假设是（ ）。 A．很多学生参加了古文训练班 B．学生的父母应该教给学生一些 C．语文成绩的提高与参加古文训练班没有必然的联系 D．只有参加古文训练才能够提高语文成绩
正确答案：D
题干的假设是，必须只有“参加古文训练”这一种途径才“能够提高语文成绩”。故选D。
-
第14题：
甲、乙两个单位分别有60和42名职工，共同成立A、B两个业余活动小组，所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%，乙单位职工中参加B组的人数与参加A组的人数之比为3∶4，参加B组的人中，甲单位职工占5/8。问有多少人仅参加A组?A.35
B.42
C.46
D.56答案：C解析：第一步，本题考查容斥问题。
第二步，设乙单位只参加一个小组的人数为5x，则只参加A组的有5x·60%=3x名职工，那么只参加B组的有5x－3x=2x名职工，设乙单位AB组都参加的有y人。可列方程：（2x＋y）∶（3x＋y）＝3∶4，解得x＝y，那么乙单位中参加B组的有3x人，参加A组的有4x人，AB都参加的有x人，可列方程：3x＋4x－x＝42，解得x＝7，那么参加B组的有21人，只参加A组的有21人。
那么甲单位只参加A组的有60－35＝25（人），那么两个单位只参加A组的有21＋25＝46（人）。 -
第15题：
某单位工会会员60 人，现在组织会员报名参加兴趣活动小组，其中报名徒步组的有40 人，羽毛球组的有38 人，乒乓球组的有31 人，这三项活动都报名的有18 人，问这个单位工会会员中最多有多少人三个小组都没有报名？A.14
B.15
C.16
D.18答案：A解析：
-
第16题：
某校共有三个兴趣小组，分别为体育、书法和美术。巳知参加这三个兴趣小组的学生分别 是25人、24人、30人。同时参加体育、书法兴趣小组的有5人，同时参加体育、美术兴趣 小组的有2人，同时参加书法、美术兴趣小组的有4人，有1人同时参加这三个兴趣小组， 共有（ ）人参加兴趣小组。
A. 74 B. 72 C. 70 D. 69答案：D解析：根据文氏图：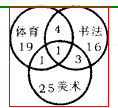
可得三个兴趣小组的总人数为25 + 24 + 30—(5 + 2 + 4) + 1==69(人）。所以答案选D。 -
第17题：
两组学生，其中一组参加了古文训练班，另一组没有参加，在语文考试中，参加过古文训练班的学生比那些没有参加过的学生的平均分数高很多，因此，要想让学生在语文考试中的成绩提高，就必须让他们参加古文训练班。下列是上述论证以来的假设是：
A. 很多学生参加了古文训练班
B. 学生的父母应该教给学生一些
C. 语文成绩的提高与参加古文训练班没有必然的联系
D. 只有参加古文训练才能够提高语文成绩答案：D解析：解题指导： 题干的假设必须是只有“参加古文训练”这一途径才“能够提高语文成绩”，若父母的教授也能提高语文成绩，就退不出题干中的结论。故答案为D。 -
第18题：
如果乙与丁都没有参加台球组，则可以得出以下哪项？A.如果己参加台球组、则丙参加登山组
B.如果庚参加台球组，则戊参加台球组
C.如果甲参加羽毛球组，则庚参加登山组
D.如果乙参加羽毛球组，则己参加登山组答案：D解析：乒乓球组只有乙，丙，因为台球不能有乙，丁，所以丁肯定在羽毛球和登山组，题中提了，丁与戊
在一组，丁不在台球，所以甲也不在，所以甲，丁，戊都在羽毛球和登山组，一组最多五人，己和庚情况相同，所以
必定有一个在台球组，A项中丙可以去羽毛球或登山，B项中戊必须要去羽毛球和登山，C项中庚有可能参加羽毛球和
登山组，只有D正确。 -
第19题：
一次运动会上，18名游泳运动员中，有8名参加了仰泳，有10名参加了蛙泳，有12名参加了自由泳，有4名既参加仰泳又参加蛙泳，有6名既参加蛙泳又参加自由泳，有5名既参加仰泳又参加自由泳，有2名这3个项目都参加，这18名游泳运动员中，只参加1个项目的人
A.5名
B.6名
C.7名
D.4名答案：B解析：通过画集合图可知，只参加仰泳项目的有1人，只参加蛙泳项目的有2人，只参加自由泳项目的有3人，所以只参加1个项目的人有1+2+3=6人。 -
第20题：
五年级一班共有55个学生，在暑假期间都参加了特长培训班，35人参加书法班，28人参加美术班，31人参加舞蹈班，其中以上三种特长培训班都参加的有6人，则有（ ）人只参加了一种特长培训班。A.45
B.33
C.29
D.22答案：D解析：参加两种特长培训班的小朋友人数为35+28+31-2×6-66=7人，则只参加了一种特长班的人数为55-27-6=22人。 -
第21题：
88名学生参加运动会，参加游泳比赛的有23人，参加田径比赛的有33人，参加球类比赛的有54人，既参加游泳比赛又参加田径比赛的有5人，既参加田径比赛又参加球类比赛的有16人。已知每名学生最多可参加两项比赛，问只参加田径比赛的有多少人（）
- A、20
- B、17
- C、15
- D、12
正确答案:D