在（）里填上适当的数，使等式成立。 1/2+1/4=（）/（）+1/21/6+1/10+9/10=1/6+（1/10+()/()）1/12+1/4+（5/12+3/4）=（1/12+()/()）+（()/()+()/ ()）

题目

在（）里填上适当的数，使等式成立。      

1/2+1/4=（）/（）+1/2

1/6+1/10+9/10=1/6+（1/10+()/()）

1/12+1/4+（5/12+3/4）=（1/12+()/()）+（()/()+()/ ()）

相似考题

1.在下面括号里填上适当的数。7/10=14/()=()/30 3/4=()/8=9/()8/24=2/()=()/3 5/9=()/18=15/()

2.在○里填上适当的符号。789○759 5/12○7/20 1.3元○1.30元32.63○40.7 3.58○3.61 1.39吨○913千克

3.请在5个3之间填上+,-,×,÷,()使等式成立3 3 3 3 3=6

4.在括号里填上适当的数。（1）5/（）=（）/8（2）0.63：（）=（）：10

参考答案和解析

1/2+1/4=（1）/（4）+1/2

1/6+1/10+9/10=1/6+（1/10+(9)/(10)）

1/12+1/4+（5/12+3/4）=（1/12+(5)/(12)）+（(1)/(4)+(3)/(4)）


更多“在()里填上适当的数,使等式成立。 ”相关问题

  • 第1题：

    等式的左边乘，要想使等式成立，等式的右边要（ ）。


    正确答案：

    除以

  • 第2题：

    请认真阅读以下材料，并回答问题。
    练习1：请在下面各小题的括号里填上适当的数，使等式成立。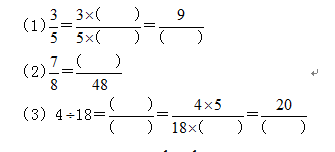

    练习2：请分别找出与?和?相等的数。

    [问题1][简答题]
    试简要说明“分数的基本性质”和“商不变性质”。（10分）

    [问题2][简答题]
    如指导高年级小学生学习“分数的基本性质”，试拟定教学目标。（8分）

    [问题3][简答题]
    根据拟定的教学目标，设计三道练习题，并说明设计意图。（22分）


    答案：
    解析：
    1、1)分数的基本性质。分数的分子和分母同时乘上或除以相同的数（0除外），分数的大小不变。
    (2)商不变的性质。被除数和除数同时扩大或缩小相同的倍数，商不变。

    2、1．知识与技能目标
    让学生通过经历“预测猜想一实验分析一合情推理一探究创造”的过程，理解和掌握分数的基本性质，知道它与整数除法中商不变性质之间的联系。
    2．过程与方法目标
    培养学生的观察能力、动手操作能力和分析概括能力。
    3．情感态度与价值观目标
    渗透事物是互相联系、发展变化的辩证唯物主义观点，使学生体会“变与不变”的思想。

    3、练习题1：你能根据分数的基本性质，再写出一组与老师所说的分数相等的分数吗？
    [设计理由]在学习主要内容之后，让学生进行练习，这是学生学习的主要途径，能够使学生进一步熟悉并掌握本课重点内容。
    练习题2：什么叫分数的基本性质呢？就你的理解，用自己的语言说一说。
    [设计理由]通过学生自己对分数基本性质的理解和阐述，培养他们分析和抽象概括的能力，以及语言表达能力。
    练习题3：请大家拿出1张长方形纸片，把它对折平均分成4份，涂出其中的3份，写上分数。再把它继续对折平均分成8份，看看原来的现在成了多少。继续折成16份，看看原来的现在又成了多少。
    [设计理由]通过学生的动手操作，直观形象地看出分数的基本性质，引发学生的思考和疑问，引导学生体会“变与不变”的思想。

  • 第3题：

    根据后面的提示，在括号里填上适当的疑问词，完成句子。 今（）ですか。（9時）


    11

  • 第4题：

    如果向量β可由向量组a1,a2,…,as线性表示，则下列结论中正确的是：
    A.存在一组不全为零的数k1,k2,…,ks使等式β=k1a1+k2a2+...+ksas成立
    B.存在一组全为零的数k1,k2,…,ks使等式β=k1a1+k2a2+...+ksas成立
    C.存在一组数k1,k2,…,ks使等式β=k1a1+k2a2+...+ksas成立
    D.对β的线性表达式唯一


    答案：C
    解析：
    提示：向量β能由向量组a1,a2,…,as线性表示，仅要求存在一组数k1,k2,…,ks使等式β=k1a1+k2a2+...+ksas成立，而对k1,k2,…,ks是否为零并没有做规定，故选项A、B排除。 若β的线性表达式唯一，则要求a1,a2,…,as线性无关，但题中没有给出该条件，故D也不成立。

  • 第5题：

    请认真阅读以下材料，并回答问题。
    练习1，请在下面各小题的括号里填上适当的数，使等式成立。

    问题（一）：试简要说明“分数的基本性质”和“商不变性质”。
    问题（二）：如指导高年级小学生学习“分数的基本性质”，试拟定教学目标。
    问题（三）：根据拟定的教学目标，设计三道练习题，并说明设计意图。


    答案：
    解析：
    【参考设计】问题（一）：（1）分数的基本性质。分数的分子和分母同时乘上或除以相同的数（0除外），分数的大小不变。（2）商不变的性质。被除数和除数同时扩大或缩小相同的倍数，商不变。
    问题（二）：
    1.知识与技能目标
    让学生通过经历“预测猜想-实验分析-合情推理-探究创造”的过程，理解和掌握分数的基本性质，知道它与整数除法中商不变性质之间的联系。
    2.过程与方法目标
    培养学生的观察能力、动手操作能力和分析概括能力。
    3.情感态度与价值观目标
    渗透事物是互相联系、发展变化的辩证唯物主义观点，使学生体会“变与不变”的思想。
    问题（三）
    练习题1:你能根据分数的基本性质，再写出一组与老师所说的分数相等的分数吗？
    [设计理由]在学习主要内容之后，让学生进行练习，这是学生学习的主要途径，能够使学生进一步熟悉并掌握本课重点内容。
    练习题2:什么叫分数的基本性质呢？就你的理解，用自己的语言说一说。
    [设计理由]通过学生自己对分数基本性质的理解和阐述，培养他们分析和抽象概括的能力，以及语言表达能力。
    练习题3:请大家拿出1张长方形纸片，把它对折平均分成4份，涂出其中的3份，写上分数。再把它继续对折平均分成8份，看看原来的3/4现在成了多少。继续折成16份，看看原来的3/4现在又成了多少。
    [设计理由]通过学生的动手操作，直观形象地看出分数的基本性质，引发学生的思考和疑问，引导学生体会“变与不变”的思想。

相关内容