有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为()A、w0B、Jw0/mR^2C、Jw0/(J+mR^2)D、Jw0/(J+2mR^2)
题目
有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为()
A、w0
B、Jw0/mR^2
C、Jw0/(J+mR^2)
D、Jw0/(J+2mR^2)
相似考题
更多“有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为() ”相关问题
-
第1题：
图4-67示均质圆轮，质量为m,半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为（ ）。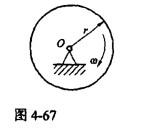
答案：A解析：提示：根据动量、动量矩、动能的定义，刚体作定轴转动时，ρ = mvc、LO= JOω, T=1/2JOω2。 -
第2题：
均质圆盘的质量为m，半径为r，若圆盘绕圆盘边缘上的轴A（轴A垂直于圆盘面)以角速度ω 转动时，其动能无法计算
A 解析： -
第3题：
在绕通过盘心且垂直于盘面的转轴自由旋转的水平圆盘边上，站着一质量为m的人。圆盘的半径为R，转动惯量为J，角速度为w 。已知m×R×R=2J。如果这人由盘边走到盘心，则角速度变为原来的几倍？
C[解题过程] 对于此系统来说，并无外力矩作用，故系统对轴O的角动量守恒，故L不变，所以下式成立 mvd-mvd+J 0 ω 0 =Jω 式中mvd为子弹对点O的角动量，ω 0 为圆盘初始角速度，J为子弹留在盘中后系统对轴O的转动惯量，J 0 为子弹射入前盘对轴O的转动惯量．由于J＞J 0 ，则ω＜ ω 0．故选C． -
第4题：
闭环数控转台的结构与开环数控转台大致相同，其区别在于闭环数控转台有圆光栅或圆感应同步器转动角度测量元件。
正确 -
第5题：
一质量为m，半径为R 的匀质圆盘对过其中心与盘面垂直的轴的转动惯量为J，若在保持其质量不变的情况下，使之变成半径为2R 的匀质圆盘，则其对相同转轴的转动惯量为（）
A．因质量不变，所以转动惯量不变，仍为J
B．因半径变为2R，所以转动惯量变为2J
C．转动惯量为3J
D．转动惯量为4J
大圆的面积为S=πR 2 ，质量的面密度为ζ=M/S。大圆绕过圆心且与盘面垂直的轴线的转动惯量为IM=MR 2 /2。小圆的面积为s=πr 2 ，质量为m=ζs，绕过自己圆心且垂直圆面的轴的转动惯量为IC=mr 2 /2，根据平行轴定理，绕大圆轴的转动惯量为