曲线y=2＋lnx在点x=1处的切线方程是()A、y=x-1B、y=x+1C、y=xD、y=-x

题目
曲线y=2＋lnx在点x=1处的切线方程是()

A、y=x-1

B、y=x+1

C、y=x

D、y=-x

相似考题

1.曲线y=x+ln x在点（1，1）处的切线方程为________________.

2.曲线y=x3—2x在点（1，-1）处的切线方程为 ．

3.曲线y＝x2＋1在点(1，2)处的切线方程为__________．

4.曲线y=x3+1在点（1，2）处的切线方程是__________．

更多“曲线y=2＋lnx在点x=1处的切线方程是() ”相关问题

  • 第1题：

    已知曲线y=x3-3x2-1，过点(1，-3)作其切线，求切线方程。


    正确答案：

    y′=3x2-6x，当x=1时，y=1-3-1=-3，即点（1，-3）在曲线上。可知此切线的斜率为k=3×12-6×1=-3，由点斜式可知，此切线的方程为y-(-3)=-3(x-1)即为y=-3x。

  • 第2题：

    曲线y=2x2在点(1，2)处的切线方程y=______．


    答案：
    解析：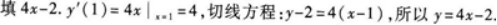

  • 第3题：

    曲线sin(xy)+ln(y-x)=x在点(0，1)处的切线方程是________.


    答案：1、y=x+1.
    解析：
    先求曲线sin(xy)+ln(y-x)=x在点(0，1)处切线斜率y'(0).等式sin(xy)+ln(y-x)=x两端对x求导得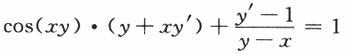

    在上式中令x=0，y=1得y'(0)=1，于是该曲线在点(0，1)处的切线方程为y-1=x，即y=x+1.

  • 第4题：

    曲线x2+y2=2x在点(1，1)处的切线方程为.


    答案：
    解析：
    【答案】y=1【考情点拨】本题考查了曲线上一点处的切线方程的知识点．
    【应试指导】由x2+y2=2x，两边对x求导得2x+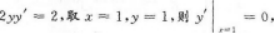

  • 第5题：

    曲线y=x3-x在点(1，0)处的切线方程y=______．


    答案：
    解析：
    填2(x-1)．因为y'=3x2-1，y'(1)=2，则切线方程为y=2(x-1)．

相关内容