某校五年级有100名学生参加活动，男生两人一组，女生三人一组，共有41组。那么男、女生各有多少名？( )A.46、54 B.48、52 C.52、48 D.54、46
题目
B.48、52
C.52、48
D.54、46
相似考题
更多“某校五年级有100名学生参加活动，男生两人一组，女生三人一组，共有41组。那么男、女生各有多少名？( )”相关问题
-
第1题：
有50名学生参加联欢会，第一个到会的女生同每个男生握过手，第二个到会的女生只差1个男生没握过手，第三个到会的女生只差2个男生没握过手，如此等等，最后一个到会的女生和7个男生握过手，那么这50名学生中有几名男生？（ ）。
A．28
B．26
C．23
D．30
正确答案：A
A 【解析】从题目中已经知道参加联欢会的男生和女生共有50名。因此，如果能知道男生人数与女生人数的差，即可按和差问题的数量关系求出男生有多少人。
为了使题目中的条件更容易分析，我们不妨将女生的顺序反过来，从后往前看。也就是说：最后一个到会的女生同7个男生握过手；倒数第二个到会的女生同8个男生握过手；倒数第三个到会的女生同9个男生握过手，如此等等，第一个到会（即倒数最后一个）的女生同全部男生握过手。由此，立即可知，男生人数比女生的人数多6个人。因此，男生人数为（50+6）÷2=28（人）。
-
第2题：
某高校的22名大学生志愿担任义务家教，他们中间既有文科生也有理科生，已知理科生比文科生多，理科男生比理科女生多，文科女生比理科男生多2人，至少有1名文科男生，那么在这22人中，共有理科女生多少人?（ ）
A．5
B．7
C．8
D．9
正确答案：A
已知在22名大学生中理科生比文科生多，那么理科生就不少于12人，文科生不多于10人；理科女生和理科男生共计不少于12人，且理科男生比理科女生多，则理科男生不少于7人；已知文科女生比理科男生多2人，则文科女生不少于7+2=9(人)；又因为文科生不多于10人，可得出文科男生至多有1人。但题中指出，至少有1名文科男生，由此可以确定文科男生是1人，那么文科女生就不多于9人，前面已有结论，文科女生不少于9人，因此确定文科女生有9人，又因为文科女生比理科男生多2人，可知理科男生有7人，那么理科女生的人数是：22－9－1－7=5(人)。 -
第3题：
某校参加数学竞赛的有120名男生，80名女生，参加语文竞赛的有120名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科都参加了，问只参加数学竞赛而没有参加语寒竞赛的女生有多少人?（ ）
A．65
B．60
C．45
D．15
正确答案：D
依题意可知，同时参加两种竞赛的人数是(120+80)×2-260=140(人)，同时参加两种竞赛的女生人数是为140-75=65（人)．则只参加了数学而未参加语文竞赛的女生有80-65=15(人)。故选D。 -
第4题：
现从8名学生干部中选出2名男同学和1名女同学分别参加全校“资源”、“生态”和“
环保”三个夏令营活动，已知共有90种不同的方案，那么男、女同学分别有A: 男生5人，女生3人
B: 男生3人，女生5人
C: 男生6人，女生2人
D: 男生2人，女生6人答案：B解析：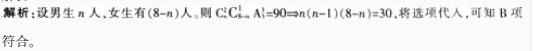
-
第5题：
教室里有若干学生，走了10名女生后，男生人数是女生的2倍，又走了9名男生后，女生人数是男生的5倍，问最初教室里有多少人？（ ）
A15
B20
C25
D30答案：C解析：解析1：
假设教室里最初有名女生，有名男生，那么根据条件：走了10名女生后，男生是女生的2倍，可列出方程式：
；
又走了9名男生后，女生是男生的5倍可知：
；
联立可得，，所以最初教室里有人数。
解析2：
走了10名女生后，女生 ：男生＝1:2＝5:10；走了9名男生后，女生：男生＝5:1，可见男生刚好减少9份，每份1人，则走了9名男生后，男生人数为1人，女生人数为5人，故原有男生10人，女生，所以最初教室里有。
故正确答案为C。 -
第6题：
育红小学六年级选出的男生的
和12名女生参加数学竞赛，剩下的男生人数是剩下的女生人数的2倍。已知六年级共有156人，问男、女生各有多少人？（ ）
A. 99，57
B. 96，60
C. 86，70
D. 80，76答案：A解析：
-
第7题：
单选题一个年级有男生女生若干人，讨论分组时，一组有5个男生、3个女生，则分为N组后，还剩8个男生；若换一种分法：一组有7个男生、3个女生，则分为M组后，还剩24个女生。问这个年级共有多少学生（）A264
B274
C282
D284
正确答案： B解析： 根据题意可得，总人数能被8整除，结合选项，只有A满足题意。 -
第8题：
某校参加数学竞赛的有l20名男生.80名女生，参加语文竞赛的有l20名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75.名男生两科都参加了，则只参加数学竞赛而没有参加语文竞赛的女生有( )。
A.65人 B.60人 C.45人 D.15人
正确答案：D共有(120+80)×2—260—140人同时参加两科竞赛，其中女生人数是140—75=5人。那么只参加数学竞赛的女生有80—65=l5人。
-
第9题：
某校参加数学竞赛有120名男生、80名女生，参加语文竞赛有120名女生、80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科竞赛都参加了，那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
A．15
B．25
C．65
D．75
正确答案：A
[答案] A。[解析]此题为比较复杂的容斥问题，有75名男生两科竞赛都参加了，因此至少参加了一项竞赛的男生有120+80-75=125人，那么至少参加一项竞赛的女生有260-125=135人，那么只参加数学竞赛没有参加语文竞赛的女生有135-120=15人。 -
第10题：
某校有58名同学参加数学竞赛，已知将参赛人任意分成四组，则必有一组的女生多于3人，又知参赛者中任意14人中必有男生，则参赛男生的人数为：
A45
B46
C47
D48答案：A解析：
-
第11题：
某兴趣组有男女生各5名，他们都准备了表演节目。现在需要选出4名学生各自表演1个节目，这4人中既要有男生、也要有女生，且不能由男生连续表演节目。那么，不同的节目安排有多少种？A.1200
B.2400
C.3000
D.3600答案：B解析：第一步，本题考查排列组合问题，属于方法技巧类。
第二步，根据不能由男生连续表演节目可采用插空法，先从男生和女生中选取所需要的人数，然后安排女生表演节目，最后将男生的节目插入到女生的节目之间，需要考虑顺序。有以下两种情况：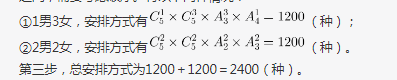
-
第12题：
—次校友聚会共有50人参加，在参加聚会的同学中，每个男生认识的女生人数各不相同，而且恰好构成一串连续的自然数。已知认识女生最少的一个男生认识15名女生，并有一名男生认识所有女生，则参加这次聚会的男生一共有：A.16 名
B.17 名
C.18 名
D.19 名答案：C解析：设共有x名男生，则有女生50-x名，认识女生最多的一名男生认识x-1+15名女生，则有x-1+15=50-x，解得x=18。 -
第13题：
某小学共有1000名学生，男生占60%，女生占40%；其中10%的学生是寄读学生。据此，下列哪种情况不可能出现？（）
- A、11%的男生和8.5%的女生是寄读生
- B、13%的男生和5.5%的女生是寄读生
- C、9%的男生和11.5%的女生是寄读生
- D、8.5%的男生和10%的女生是寄读生
正确答案:D