在平面中三角形内角和等于180度，在球面中三角形内角和大于180度，在凹面中三角形内角和小于180度，这说明（ ）。A.真理具有决定性 B.真理具有相对性 C.真理具有客观性 D.真理具有全面性

题目
在平面中三角形内角和等于180度，在球面中三角形内角和大于180度，在凹面中三角形内角和小于180度，这说明（ ）。

A.真理具有决定性
B.真理具有相对性
C.真理具有客观性
D.真理具有全面性
相似考题

1.欲确定一个平面三角形至少需要观测其几个内角()。A、一个内角B、两个内角C、三个内角。

2.三角形内角之和等于180°，这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里，人们一直把看作它任何条件下都适用的真理。但是，19世纪初，俄国数学家罗巴切夫斯基提出：在凹曲面上、三角形内角之和小于180。，随后，德国数学家黎曼提出：在球形凸面上，三角形内角之和大于180°。这说明真理是（ ）。 A．因人而异的 B．具体的 C．有条件的 D．客观的

3.如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角如果三角形的一个外角等于和它相邻的内角的４倍，等于与它不相邻的一个内角的２倍，则此三角形各内角的度数是_____________。

4.“三角形的内角和等于180°”属于条件性知识。（ ）

参考答案和解析
答案：B
解析：
真理的相对性，即相对真理，是指真理的有条件性、有限性，即在一定条件下，人们对事物的客观过程及其发展规律的正确认识总是有局限的、不完全的。三角形内角之和等于180度，但是，在凹面上，三角形内角之和小于180度，而在球形凸面上，三角形内角之和大于180度，这说明任何真理都有自己适用的条件和范围，真理是有条件的、有限的。任何真理都只能是主观对客观事物近似正确即相对正确的反映。故本题选B。
更多“在平面中三角形内角和等于180度，在球面中三角形内角和大于180度，在凹面中三角形内角和小于180度，这说明（ ）。”相关问题

  • 第1题：

    公元前3世纪,古希腊数学家欧几里得提出:“三角形内角之和等于180度。”19世纪德国数学家黎曼提出:“在球面上,三角形内角之和大于180度。”后来,俄国数学家罗巴切夫斯基又提出:“在凹面上,三角形内角之和小于180度。”这一认识过程说明

    A.真理具有客观性
    B.真理具有相对性
    C.真理具有绝对性
    D.真理具有唯一性

    答案：B
    解析：
    第一步，本题考查哲学。第二步，三角形内角和在不同的条件下，会等于180°或大于小于180°说明真理是有条件的、具体的，即真理具有相对性。任何真理都有自己适用的条件和范围。真理和谬误有严格的界限。真理和谬误的界限在于是否正确的反映了客观实际及其规律，二者作为一对矛盾，在真理不断发展的过程中不断解决，同时又不断产生，推动着认识的不断发展。任何真理都有自己的适用条件和范围，任何真理都是相对于特定的过程来说，如果超越了真理的适用条件、范围和过程，真理就会转化为谬误。因此，选择B选项。A项：真理的客观性是指真理的内容是客观的，检验真理的唯一标准——实践也是客观的，与题意不符。C项：真理的绝对性是指在特定的条件和范围之内，真理是绝对的，永远不能被推翻，与题意不符。D项：真理在特定的范围之内，才具有唯一性，与题意不符。

  • 第2题：

    观测三角形内角3次，求得三角形闭合差分别为+8″、-10″和+2″，则三角形内角和的中误差为（　　）。

    A、±6.7″
    B、±7.5″
    C、±9.2″
    D、±20″

    答案：B
    解析：
    中误差是指有限次观测的偶然误差求得的标准差，即三角形内角和的中误差为：

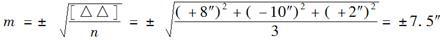
  • 第3题：

    对某一三角形的内角进行观测，其内角和为180°00′03″.则此次观测的三角形内角和真误差值为3″。


    正确答案:正确

  • 第4题：

    球面三角形三内角之和小于180°。


    正确答案:错误

  • 第5题：

    在哪个几何体系中三角形三内角之和等于180度（）


    正确答案:欧氏几何

  • 第6题：

    在哪个几何体系中三角形三内角之和大于180度（）


    正确答案:黎曼几何

  • 第7题：

    单选题
    在平面中三角形内角和等于180°，但在球面中，三角形内角和大于180°，在凹面中内角和小于180°。这说明（）。
    A

    真理具有绝对性

    B

    真理具有相对性

    C

    真理具有客观性

    D

    真理具有全面性


    正确答案： C
    解析： 暂无解析

  • 第8题：

    填空题
    在哪个几何体系中三角形三内角之和大于180度（）

    正确答案： 黎曼几何
    解析： 暂无解析

  • 第9题：

    填空题
    在哪个几何体系中三角形三内角之和等于180度（）

    正确答案： 欧氏几何
    解析： 暂无解析

  • 第10题：

    判断题
    球面三角形三内角之和小于180°。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    如果一个三角形的两个内角度数的和等于第三个内角的度数，那么这个三角形是（）。
    A

    钝角三角形

    B

    锐角三角形

    C

    直角三角形

    D

    无法判断


    正确答案： A
    解析： 暂无解析

  • 第12题：

    知道“三角形的内角和等于180°”，属于（ ） 。


    答案：陈述性知识,
    解析：
    提示：请参考答案，输入的答案要和答案显示，有“，”“《》” ”“ 一模一样才会显示正确。

  • 第13题：

    初中数学《三角形内角和》
    一、考题回顾
    题目来源:5月18日 上午 吉林省通化市 面试考题
    试讲题目
    1.题目：三角形内角和
    2.内容：




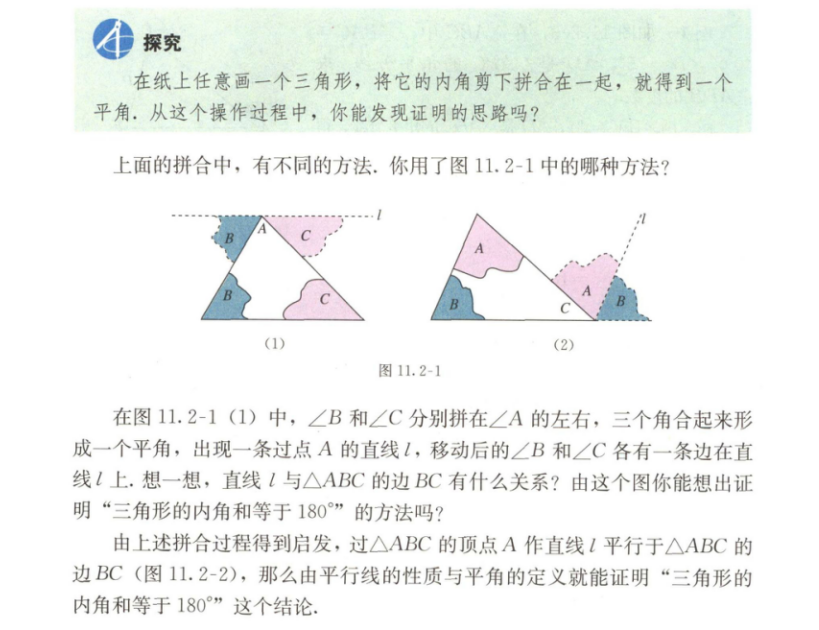
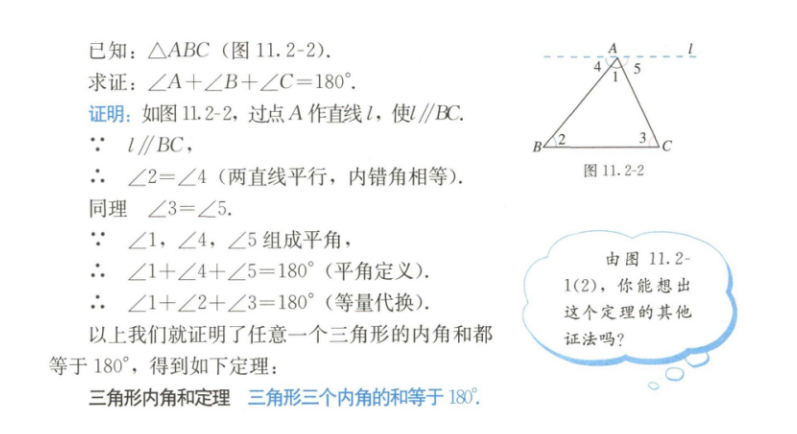
    3.基本要求：
    (1)能够证明三角形的内角和是180°，并解决相关问题。
    (2)试讲十分钟;
    (3)要有合适的板书。
    答辩题目
    1.在验证三角形的内角和的过程中运用了哪些教学方法?
    2.本节课的在教材中的地位和作用?


    答案：
    解析：
    二、考题解析
    【教学过程】
    (一)导入新课
    回顾小学阶段学习三角形内角和定理时，利用剪一剪、拼一拼的实验验证方法，通过复习导入引出课题。
    (二)新知探索
    组织学生进行小组讨论，用拼合的方法探究三角形内角和的证明思路。
    引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论，再各组派代表在全班进行交流。
    在交流的过程中出现了多种拼合方法，教师组织学生集体评价，并及时引导学生展开讨



    【答辩题目解析】
    1. 在验证三角形的内角和的过程中运用了哪些教学方法?
    【参考答案】
    在验证三角形的内角和的过程中运用了小组讨论和自主探究的教学方法。组织学生进行小组讨论，用拼合的方法探究三角形内角和的证明思路。引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论，再各组派代表在全班进行交流。然后让学生自主探究通利用数学方法证明三角形的内角和定理?通过这样的教学方法，可以充分体现学生的主体性。
    2. 本节课的在教材中的地位和作用?
    【参考答案】
    本节课选自人教版初中数学八年级上册第十一章第二节内容《三角形的内角》第一课时，它是在学生掌握了三角形的特征和分类的基础上教学的。其中三角形内角和的探索和证明过程是本节课的重要教学内容。本节课的内容又是多边形内角和的基础，具有承前启后的作用。

  • 第14题：

    材料一人类认识和把握世界的过程，也就是追求真理的过程。我们可以用纸折叠的方式来检验在平面上三角形内角之和等于180度，不管我们以前有没有认识到这一点，它都是不以人的意志为转移的，是客观存在的。我们实践中获得了平面上三角形内角之和等于180度的真理性的认识。 材料二我们知道了在平面上三角形内角之和等于180度。19世纪初，德国数学家指出：在球形凸面上，三角形内角之和大于180度。由此，人们关于空间的观念发生了革命性的转变。我们在地球仪上随意选择三点构成三角形直观感悟内角之和的情况。可以看到赤道、经线90度和0度经线构成270度的角。 材料三 随着农林畜牧业的发展、土地丈量和利用的增多，使人们逐渐确立了三角形内角之和等于180度的认识。随着航海事业的发展和人们对球面认识的不断深入，这一认识的局限性逐渐暴露出来。 19世纪初，俄国数学家提出：在凹曲面上，三角形内角之和小于180度。 这个过程受到了什么因素的制约？


    正确答案: 这个过程受到各种条件的限制，首先从主体来看，受具体实践水平的限制，还受到立场、观点、方法、知识水平、思维能力、生理素质等条件限制。其次，从客体来看，客观事物的复杂性、变化性，使其本质的暴露和展现有一个过程。

  • 第15题：

    在平面中三角形内角和等于180°，但在球面中，三角形内角和大于180°，在凹面中内角和小于180°。这说明（）。

    • A、真理具有绝对性
    • B、真理具有相对性
    • C、真理具有客观性
    • D、真理具有全面性

    正确答案:B

  • 第16题：

    在黎曼几何中，三角形三个内角和（）180度。

    • A、大于
    • B、等于
    • C、小于
    • D、以上都不对

    正确答案:A

  • 第17题：

    在正曲率空间（如球面）中，三角形三内角之和（）.

    • A、等于180度
    • B、大于180度
    • C、小于180度
    • D、等于360度

    正确答案:B

  • 第18题：

    单选题
    在正曲率空间（如球面）中，三角形三内角之和（）.
    A

    等于180度

    B

    大于180度

    C

    小于180度

    D

    等于360度


    正确答案： C
    解析： 暂无解析

  • 第19题：

    单选题
    在黎曼几何中，三角形三个内角和（）180度。
    A

    大于

    B

    等于

    C

    小于

    D

    以上都不对


    正确答案： D
    解析： 暂无解析

  • 第20题：

    单选题
    张老师是一名小学数学教师，他想讲授三角形形状与内角和之间的变化，以下哪些描述更适合他使用（）
    A

    使用几何画板动态演示三角形变化与内角和之间的关系

    B

    让学生在几何画板中体验三角形形状与内角和之间的关系

    C

    提供多种三角形形状，让学生探索三角形形状与内角和之间的关系

    D

    提供一些资源，让学生证明三角形内角和与形状间的关系


    正确答案： C
    解析： 暂无解析

  • 第21题：

    单选题
    三角形内角之和等于180°。但是，在凹曲面上，三角形内角之和小于180°，而在球形凸面上，三角形内角之和大于180°。这说明（  ）。①真理和谬误往往是相伴而行的②真理是有条件的、具体的③对同一个确定对象的认识可以有多个真理④任何真理都有自己适用的条件和范围
    A

    ①④

    B

    ②③

    C

    ①③

    D

    ②④


    正确答案： D
    解析：

  • 第22题：

    单选题
    欲确定一个平面三角形至少需要观测其几个内角（）。
    A

    一个内角；

    B

    两个内角；

    C

    三个内角。


    正确答案： B
    解析： 暂无解析

相关内容