设函数f(x)在 内连续，其导函数的图形如图所示，则f(x)有 A.一个极小值点和两个极大值点 B.两个极小值点和一个极大值点 C.两个极小值点和两个极大值点 D.三个极小值点和一个极大值点

题目
设函数f(x)在 内连续，其导函数的图形如图所示，则f(x)有

A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点
相似考题

1.设f(x)为连续函数，F(x)是f(x)的原函数，则（ ）。(A) 当f(x)是奇函数时，F(x)必为偶函数(B) 当f(x)是偶函数时，F(x)必为奇函数(C) 当f(x)是周期函数时，F(x)必为周期函数(D) 当f(x)是单增函数时，F(x)必为单增函数(E) 当f(x)是单减函数时，F(x)必为单减函数

2.设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().A.F(z)=F（-x） B.F(x)=F（-x） C.F(X)=F（-x） D.f(x)=f（-x）

3.设函数f(x)在x=a的某个邻域内连续，且f(a)为其极大值，则存在δ＞0，当x∈(a-δ，a+δ)时，必有( )。A.(x-a)[f(x)-f(a)]≥0 B.(x-a)[f(x)-f(a)]≤0 C. D.

4.设函数f（x）在x=a的某个邻域内连续，且f（a）为极大值，则存在δ＞0，当x∈（a-δ，a+δ）时，必有（ ）

更多“设函数f(x)在 内连续，其导函数的图形如图所示，则f(x)有 ”相关问题

  • 第1题：

    设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）

    A.f（a）=0且f′（a）=0
    B.f（a）=0且f′（a）≠0
    C.f（a）＞0且f′（a）＞
    D.f（a）＜0且f′（a）＜

    答案：B
    解析：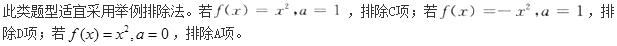

  • 第2题：

    设函数f（x）连续，则下列函数中必为偶函数的是（ ）



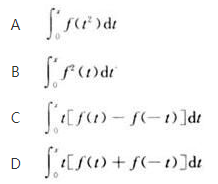    答案：D
    解析：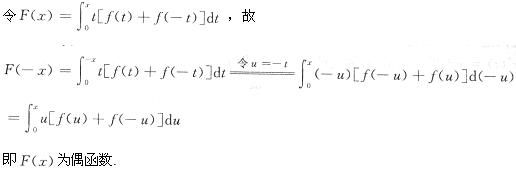

  • 第3题：

    设f(x)的一个原函数是arctanx，则f(x)的导函数是（）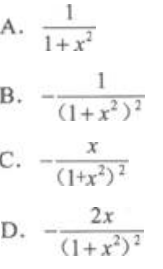


    答案：D
    解析：
    根据原函数的定义可知

  • 第4题：

    设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求


    答案：
    解析：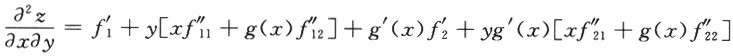

    所以，令x=y=1，且注意到g(1)=1，g'(1)=0，得

  • 第5题：

    (Ⅰ)证明拉格朗日中值定理：若函数f(x)在［a，b］上连续，在(a，b)内可导，则存在ξ∈(a，b)，使得f(b)-f(a)=f'(ξ)(b-a)；(Ⅱ)证明：若函数f(x)在x=0处连续，在(0，δ)(δ>0)内可导，且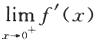=A，则存在，且.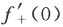


    答案：
    解析：

  • 第6题：

    设f（x）为区间[a，b]上的连续函数，则曲线y=f（x）与直线x=a，x=b，y=0所围成的封闭图形的面积为（ ）.《》（ ）


    答案：B
    解析：
    本题考查的知识点为定积分的几何意义.由定积分的几何意义可知应选B.常见的错误是选C.如果画个草图，则可以避免这类错误.

  • 第7题：

    设函数f(x)在(一∞，+∞)内连续，其中二阶导数f”(x)的图形如图所示，则曲线y(x)的拐点的个数为( )个。

    A、0
    B、1
    C、2
    D、3

    答案：C
    解析：
    拐点出现在二阶导数等于零，或二阶导数不存在的数，并且在这点的左右两侧二阶导函数异号。因此，由f”(x)的图形可得，曲线y=(x)存在两个拐点。

  • 第8题：

    设f(x)有连续导函数，（


    答案：A
    解析：
    本题考核的是不定积分的性质：“先求导后积分作用抵消”．
    前后两种运算不是对同一个变量的运算，因此不能直接利用上述性质．必须先变形，再利用这个性质．

  • 第9题：

    设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是偶函数时，下面结论正确的是（）。

    • A、F（x）是偶函数
    • B、F（x）是奇函数
    • C、F（x）可能是奇函数，也可能是偶函数
    • D、F（x）是否是偶函数不能确定

    正确答案:D

  • 第10题：

    填空题
    设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝____。

    正确答案： 2e3
    解析：
    因f′（x）＝ef（x）方程两边对x求导，得f″（x）＝ef（x）·f′（x）＝ef（x）·ef（x）＝e2f（x），两边再对x求导，得f‴（x）＝e2f（x）·2f′（x）＝2e2f（x）·ef（x）＝2e3f（x）。又f（2）＝1，则f‴（2）＝2e3f（2）＝2e3。

  • 第11题：

    填空题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

    正确答案： 1/sin2(sin1)
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第12题：

    单选题
    设f（x）是连续的偶函数，则其原函数F（x）一定是（　　）。
    A

    偶函数

    B

    奇函数

    C

    非奇非偶函数

    D

    有一个是奇函数


    正确答案： C
    解析：
    奇函数的导函数是偶函数，但是偶函数的积分不一定是奇函数，因为积分后面要加一个C，C不为0时，为非奇非偶函数；若C＝0，则为奇函数，故F（x）一定有一个是奇函数。

  • 第13题：

    设F(x)是连续函数f(x)的一个原函数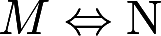，表示“M的充分必要条件是N”，则必有

    AF(x)是偶函数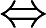f(x)是奇函数
    BF(x)是奇函数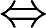f(x)是偶函数
    CF(x)是周期函数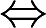f(x)是周期函数
    DF(x)是单调函数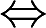f(x)是单调函数


    答案：A
    解析：

  • 第14题：

    设F（x）是连续函数f（x）的一个原函数，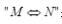

    表示“M的充分必要条件是N”，则必有（　　）。

    A．F（x）是偶函数f（x）是奇函数
    B．F（x）是奇函数f（x）是偶函数
    C．F（x）是周期函数f（x）是周期函数
    D．F（x）是单调函数f（x）是单调函数

    答案：A
    解析：

  • 第15题：

    设f(x)是连续函数，
    　　(Ⅰ)利用定义证明函数可导，且F’(x)=f(x)；
    　　(Ⅱ)当f(x)是以2为周期的周期函数时，证明函数也是以2为周期的周期函数.


    答案：
    解析：



  • 第16题：

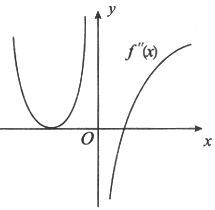
    设函数f(x)在(-∞，+∞)内连续，其二阶导函数f"(x)的图形如图所示，则曲线y=f(x)的拐点个数为
    　　

    A.A0
    B.1
    C.2
    D.3

    答案：C
    解析：
    由如图知f"(x1)=f"(x2)=0，f"(0)不存在，其余点上二阶导数f"(x)存在且非零，则曲线y=f(x)最多三个拐点，但在x=x1的两侧二阶导数不变号.因此，不是拐点，而在x=0和x=x2的两侧二阶导数变号，则曲线y=f(x)有两个拐点，故应选(C).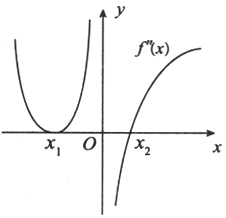　　

  • 第17题：

    下列命题中，正确的是( ).

    A.单调函数的导函数必定为单调函数
    B.设f´(x)为单调函数，则f(x)也为单调函数
    C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
    D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

    答案：D
    解析：
    可导函数的极值点必定是函数的驻点，故选D.

  • 第18题：

    设其中g(x)是有界函数，则f(x)在x=0点( )。

    A、极限不存在
    B、极限存在但不连续
    C、连续、但不可导
    D、可导

    答案：D
    解析：

  • 第19题：

    设f(x)是连续函数，F(x)是f(x)的原函数，则（）。
    A.当f(x)是奇函数时，F(x)必是偶函数
    B.当f(x)是偶函数时，F(x)必是奇函数
    C.当f(x)是周期函数时，F(x)必是周期函数
    D.当f(x)是单调增函数时，F(x)必是单调增函数


    答案：B
    解析：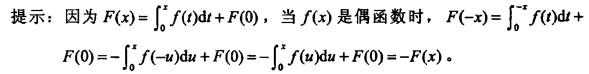

  • 第20题：

    设函数在（a，b）内连续，则在（a，b）内（）。

    • A、f（x）必有界
    • B、f（x）必可导
    • C、f（x）必存在原函数
    • D、D.必存在一点ξ∈（a，，使f（ξ）=0

    正确答案:C

  • 第21题：

    设函数f(x)=丨x丨，则函数在点x=0处（）

    • A、连续且可导
    • B、连续且可微
    • C、连续不可导
    • D、不可连续不可微

    正确答案:C

  • 第22题：

    单选题
    设函数f(x)=丨x丨，则函数在点x=0处（）
    A

    连续且可导

    B

    连续且可微

    C

    连续不可导

    D

    不可连续不可微


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
    A

    对任意x，f′（x）＞0

    B

    对任意x，f′（x）≤0

    C

    函数－f（－x）单调增加

    D

    函数f（－x）单调增加


    正确答案： A
    解析：
    令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。

  • 第24题：

    单选题
    设F（x）是连续函数f（x）的一个原函数，“M⇔N”表示“M的充分必要条件是N”，则必有（　　）。
    A

    F（x）是偶函数⇔f（x）是奇函数

    B

    F（x）是奇函数⇔f（x）是偶函数

    C

    F（x）是周期函数⇔f（x）是周期函数

    D

    F（x）是单调函数⇔f（x）是单调函数


    正确答案： C
    解析：
    采用举例的方法进行排除，令f（x）＝x，在（－∞，＋∞）内单调增加，但是F（x）＝x2/2＋C在（－∞，＋∞）内不单调，D项错误；
    令f（x）＝x2为偶函数，但是F（x）＝x3/3＋C，其中C≠0时不是奇函数，故B项错误；
    令f（x）＝1＋cosx是以2π为周期的函数，但是F（x）＝x＋sinx＋C不是周期函数，故C项错误。

相关内容