设二维随机变量(X,Y)服从二维正态分布,则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为
题目
设二维随机变量(X,Y)服从二维正态分布,则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为
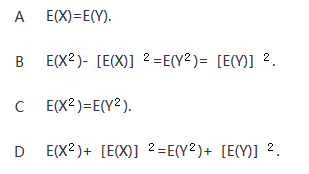
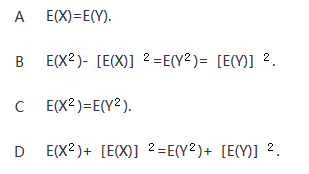
相似考题
更多“设二维随机变量(X,Y)服从二维正态分布,则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为 ”相关问题
-
第1题:
设随机变量X和Y的方差存在且不等于0,则D(X+Y)=D(X)+D(Y)是X和Y的()A.独立的必要条件,但不是充分条件;
B.独立的充分必要条件
C.不相关的充分条件,但不是必要条件
D.不相关的充分必要条件;
参考答案:D
-
第2题:
设随机变量X,Y都是正态变量,且X,Y不相关,则( ).
A.X,Y一定相互独立
B.(X,Y)一定服从二维正态分布
C.X,y不一定相互独立
D.X+y服从一维正态分布
答案:C解析:只有当(X,Y)服从二维正态分布时,X,Y独立才与X,Y不相关等价,由X,Y仅仅是正态变量且不相关不能推出X,Y相互独立,(A)不对;若X,Y都服从正态分布且相互独立,则(X,Y)服从二维正态分布,但X,Y不一定相互独立,(B)不对;当X,Y相互独立时才能推出X,Y服从一维正态分布,(D)不对,故选(C) -
第3题:
设二维随机变量(X,Y)的概率密度为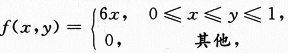 则P{X+Y≤1}=_______.答案:解析:
则P{X+Y≤1}=_______.答案:解析: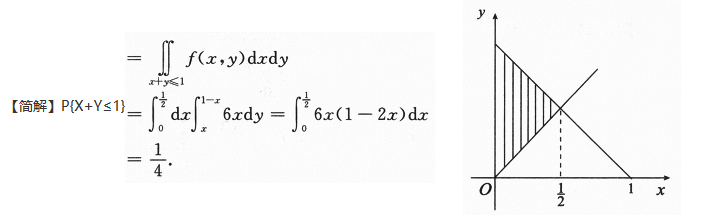
-
第4题:
设二维随机变量(X,Y)的联合密度函数为f(x,y)=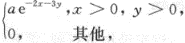 则a=_______,P(X>Y)=_______.答案:解析:
则a=_______,P(X>Y)=_______.答案:解析: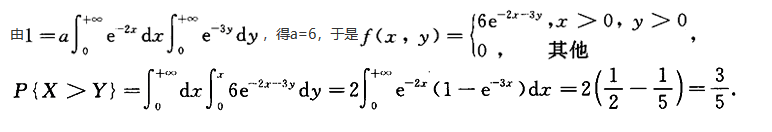
-
第5题:
设二维随机变量(X,Y)服从正态分布N(μ,μ;σ^2,σ^2;0),则E(XY^2)=________.答案:解析:
-
第6题:
设随机变量(X,Y)服从二维正态分布,其概率密度为f(x,y)=1/2π 答案:A解析:提示 (X,Y)~N(0,0,1,1,0),X~N(0,1),Y~N(0,1),E(X2+Y2) =E(X2)+E(Y2),E(X2)=D(X) + (E(X) )2
答案:A解析:提示 (X,Y)~N(0,0,1,1,0),X~N(0,1),Y~N(0,1),E(X2+Y2) =E(X2)+E(Y2),E(X2)=D(X) + (E(X) )2 -
第7题:
设随机变量X与Y相互独立且都服从区间[0,1]上的均匀分布,则下列随机变量中服从均匀分布的有()。
- A、X2
- B、X+Y
- C、(X,Y)
- D、X-Y
正确答案:C -
第8题:
设(X,Y)是二维随机变量,则随机变量U=X+Y与V=X-Y不相关的充要条件是()
- A、EX=EY
- B、EX2-(EX)2=EY2-(EY)2
- C、EX2+(EX)2=EY2+(EY)2
- D、EX2=EY2
正确答案:B -
第9题:
设随机变量X和Y相互独立,且X~N(0,1),Y~N(1,1),则()
- A、P{X+Y≤0}=0.5
- B、P{X+Y≤1}=0.5
- C、P{X-Y≤0}=0.5
- D、P{X-Y≤1}=0.5
正确答案:B -
第10题:
单选题二维随机变量(X,Y)服从二维正态分布,则X+Y与X-Y不相关的充要条件为()。AEX=EY
BEX2-[EX]2=EY2-[EY]2
CEX2=EY2
DEX2+[EX]2=EY2+[EY]2
正确答案: B解析: 暂无解析 -
第11题:
单选题设随机变量X和Y都服从正态分布,则( )。AX+Y一定服从正态分布
BX和Y不相关与独立等价
C(X,Y)一定服从正态分布
D(X,-Y)未必服从正态分布
正确答案: C解析:
用排除法,令Y=-X,则X+Y=0不服从正态分布,故排除A项;
只有X,Y的联合分布服从正态分布时,X,Y不相关才与X,Y相互独立等价,故排除B项;
一般边缘分布不决定联合分布,故选排除C项;故应选D。 -
第12题:
单选题设随机变量(X,Y)服从二维正态分布,且X与Y不相关,fX(x),fY(y)分别表示X,Y的概率密度,则在Y=y的条件下,X的条件概率密度fX|Y(x|y)为( )。AfX(x)
BfY(y)
CfX(x)fY(y)
DfX(x)/fY(y)
正确答案: D解析:
因为(X,Y)服从二维正态分布,且相关系数ρ=0,故X,Y相互独立,故fX|Y(x|y)=f(x,y)/fY(y)=fX(x)fY(y)/fY(y)=fX(x)。 -
第13题:
设随机变量X和Y都服从正态分布,则().A.X+Y一定服从正态分布
B.(X,Y)一定服从二维正态分布
C.X与Y不相关,则X,Y相互独立
D.若X与Y相互独立,则X-Y服从正态分布答案:D解析:若X,Y独立且都服从正态分布,则X,Y的任意线性组合也服从正态分布,选(D). -
第14题:
设二维随机变量(X,Y)服从二维正态分布,且X~N(1,3^2),Y~N(0,4^2),且X,Y的相
关系数为- ,又设Z=
,又设Z=
(1)求E(Z),D(Z);(2)求 ;(3)X,Z是否相互独立?为什么?答案:解析:【解】(1)
;(3)X,Z是否相互独立?为什么?答案:解析:【解】(1)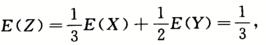

(2)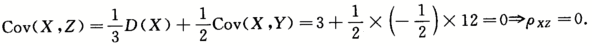
(3)因为(X,Y)服从二维正态分布,所以Z服从正态分布,同时X也服从正态分布,又X,
Z不相关,所以X,Z相互独立. -
第15题:
设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2,与y=0所围成的三角形区域.
(Ⅰ)求X的概率密度fx(x);
(Ⅱ)求条件概率密度.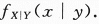 答案:解析:
答案:解析:
-
第16题:
设二维离散型随机变量(X,Y)的概率分布为
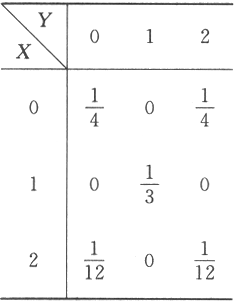
(Ⅰ)求P{X=2Y);
(Ⅱ)求Cov(X-Y,Y).答案:解析:
-
第17题:
设二维随机变量(X,Y)服从正态分布N(1,0;1,1;0),则P{XY-Y<0}=_________.答案:解析:(X,Y)~N(1,0;1,1;0),所以X与Y相互独立,且X~N(1,1),Y~N(0,1)也就有(X-1)~N(0,1)与Y相互独立,再根据对称性:P{X-1<0}=P{X-1>0}=P(Y<0)=P{Y>0}= .不难求出P{XY-Y<0}的值.
.不难求出P{XY-Y<0}的值.
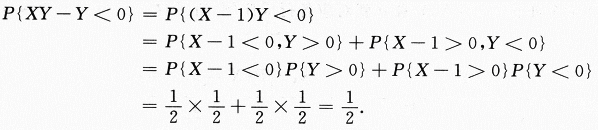
-
第18题:
设随机变量X和Y独立同分布,记U=X-Y,V=X+Y,则随机变量U与V也( )。《》( )A.不独立;
B.独立;
C.相关系数不为零;
D.相关系数为零。答案:D解析: -
第19题:
设随机变量X与Y的期望和方差存在,且D(X-Y)=DX+DY,则下列说法哪个是不正确的()。
- A、D(X+Y)=DX+DY
- B、E(XY)=EX*EY
- C、X与Y不相关
- D、X与Y独立
正确答案:D -
第20题:
设X服从0—1分布,P=0.6,Y服从λ=2的泊松分布,且X,Y独立,则X+Y().
- A、服从泊松分布
- B、仍是离散型随机变量
- C、为二维随机向量
- D、取值为0的概率为0
正确答案:B -
第21题:
设随机变量X的概率密度为fX(x),随机变量Y的概率密度为fY(y),则二维随机变量(X、Y)的联合概率密度为fX(x)fY(y)。
正确答案:错误 -
第22题:
单选题设两个相互独立的随机变量X和Y分别服从于N(0,1)和N(1,1),则( )。AP{X+Y≤0}=1/2
BP{X+Y≤1}=1/2
CP{X-Y≤0}=1/2
DP{X-Y≤1}=1/2
正确答案: B解析:
令Z=X+Y,则Z~N(1,2),则P{Z≤1}=1/2。 -
第23题:
单选题随机变量X、Y都服从正态分布且不相关,则它们( )。A一定独立
B(X,Y)一定服从二维正态分布
C未必独立
DX+Y服从一维正态分布
正确答案: D解析:
只有当随机变量X,Y的联合分布是二维正态分布时,才能保证它们“不相关”与“独立”等价。当X,Y都服从正态分布且不相关时,它们的联合分布未必是二维正态分布,X+Y也未必服从一维正态分布。
