设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆 B.矩阵A的迹为零 C.特征值-1,1对应的特征向量正交 D.方程组AX=0的基础解系含有一个线性无关的解向量

题目

设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().

A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量

相似考题

1.设三阶实对称矩阵的特征值为3,3,0,则A的秩r(A)=()A、2B、3C、4D、5

2.设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=()A、-1B、-2C、1D、2

3.设A为三阶方阵,其特征值为1,－1,2,则A^2的特征值为1,1,4。()此题为判断题(对，错)。

4.设三阶矩阵A的特征值为1,1,2,则2A＋E的特征值为()。A、3，5B、1，2C、1，1，2D、3，3，5

参考答案和解析

答案：C

解析：

由λ1=-1，λ2=0，λ3=1得|A|=0，则r(A)小于3，即A不可逆，(A)正确；又λ1+λ2+λ3=tr(A)=0，所以(B)正确；因为A的三个特征值都为单值，所以A的非零特征值的个数与矩阵A的秩相等，即r(A)=2，从而AX=0的基础解系仅含有一个线性无关的解向量，(D)是正确的；(C)不对，因为只有实对称矩阵的不同特征值对应的特征向量正交，一般矩阵不一定有此性质，所以选(C).

更多“设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().”相关问题

第1题：

三阶矩阵A的特征值为－2,1,3,则下列矩阵中为非奇异矩阵的是().

A.2E-A
B.2E+A
C.E-A
D.A-3E

参考答案：
第2题：

设A为可逆矩阵，则下列结论不正确的是( )。

A、(A-1)-1=A
B、|A-1|=|A|-1
C、(KA)-1=KA-1(k≠0)
D、(A')-1=(A-1)'

答案：C
解析：
根据逆矩阵的性质，(A)、(B)、(D)都正确，选项(C)应为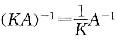
第3题：

设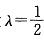是非奇异矩阵A的特征值，则矩阵（2A3）- 1有一个特征值为：

A.3
B.4
C.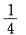
D.1

答案：B
解析：
提示：利用矩阵的特征值与矩阵的关系的重要结论：设λ为A的特征值，则矩阵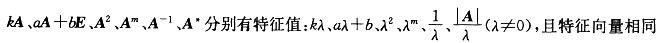
第4题：

已知n阶可逆矩阵A的特征值为λ0，则矩阵(2A)-1的特征值是：

答案：C
解析：
第5题：

设λ=1/2是非奇异矩阵A的特征值，则矩阵(2A3)-1有一个特征值为：
A. 3 B.4 C.1/4 D. 1

答案：B
解析：
提示:利用矩阵的特征值与矩阵的关系的重要结论:设λ为A的特征值，则矩阵kA、aA +bE、A2、Am、A-1 、A*分别有特征值:kλ、aλ+b、λ2、λm、1/λ、 A /λ，且特征向量相同(其中a，b为不等于0的常数，m为正整数)。
矩阵(2A3)-1对应的特征值应是矩阵2A3对应特征值的倒数，下面求矩阵2A3对应的特征值。已知λ=1/2是非奇异矩阵A的特征值，矩阵A3对应的特征值为矩阵A对应的特征值λ=1/2的三次方(1/2)3 ，矩阵2A3对应的特征值为2(1/2)3 =1/4，从而(2A3)-1对应的特征值为1/(1/4)=4。
第6题：

设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.

答案：
解析：
第7题：

设A为二阶矩阵，α1，α2为线性无关的二维列向量，Aα1=0，Aα2=2α1+α2，则A的非零特征值为________.

答案：1、1.
解析：
第8题：

设A为三阶实对称矩阵，如果二次曲面方程
　　
　　在正交变换下的标准方程的图形如图所示，
　　
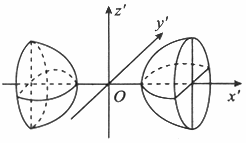
　　则A的正特征值的个数为

A.A0
B.1
C.2
D.3

答案：B
解析：
本题把线性代数与解析几何的内容有机的联系起来，首先要明白所给图形是什么曲面？其标准方程是什么？　　双叶双曲面，标准方程是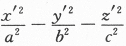：=1其次，二次型经正交变换化为标准形时，其平方项的系数就是A的特征值，所以应选(B).
很多考生选择(C)，是不是把标准方程记成了图1}　而忽略了本题的条件是x^TAx=1.
第9题：

设A为3阶矩阵，a1,a2为A的分别属于特征值-1,1的特征向量，向量a3满足

答案：
解析：
第10题：

设λ1，λ2是矩阵A的两个不同的特征值，对应的特征向量分别为a1，a2，则a1，A(a1+a2)线性无关的充分必要条件是( )。

A.λ1=0

B.λ2=0

C.λ1≠0

D.λ2≠0

答案：D
解析：
第11题：

已知λ=2是三阶矩阵A的一个特征值，α1，α2是A的属于λ=2的特征向量。若α1=（1，2，0）T，α2=（1，0，1）T，向量β=（-1，2，-2）T，则Aβ等于（）。
- A、（2，2，1）T
- B、（-1，2，_2）T
- C、（-2，4，-4）T
- D、（-2，-4，4）
正确答案:C
第12题：

单选题
已知n阶可逆矩阵A的特征值为λ0，则矩阵（2A）－1的特征值是（　　）。[2012年真题]
A
2/λ₀
B
λ₀/2
C
1/（2λ₀）
D
2λ₀

正确答案： D
解析：
由矩阵特征值的性质，2A的特征值为2λ₀，因此（2A）^－¹的特征值为1/（2λ₀）。
第13题：

A为三阶矩阵，λ₁,λ₂,λ₃为其特征值,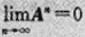的充分条件是().
A.|λ₁|=1,|λ₂|<<1,|λ₃|<1
B.|λ₁|<1,|λ₂|=|λ₃|=1
C.|λ₁|<1,|λ₂|<1,|λ₃|<1
D.|λ₁|=|λ₂|=|λ₃|=1

参考答案：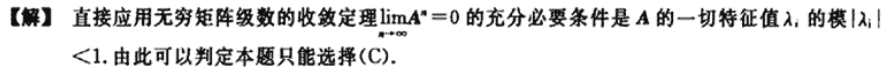
第14题：

设三阶矩阵A: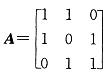，则A的特征值是:

A.1，0，1
B.1，1，2
C.-1，1，2
D.1，-1，1

答案：C
解析：
第15题：

设A,B为n阶对称矩阵,下列结论不正确的是().

A.AB为对称矩阵
B.设A,B可逆,则A^-1+B^-1为对称矩阵
C.A+B为对称矩阵
D.kA为对称矩阵

答案：A
解析：
第16题：

设A,B为三阶矩阵,且特征值均为-2,1,1,以下命题：
　　(1)A～B；(2)A,B合同；(3)A,B等价；(4)｜A｜=｜B｜中正确的命题个数为().

A.1个
B.2个
C.3个
D.4个

答案：B
解析：
因为A，B的特征值为-2，1，1，所以|A|=|B|=-2，又因为r(A)=r(B)=3，所以A，B等价，但A，B不一定相似或合同，选(B).
第17题：

设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,
　　对应特征向量为(-1,0,1)^T.
　　(1)求A的其他特征值与特征向量；
　　(2)求A.

答案：
解析：
第18题：

设A=(α1，α2，α3)为3阶矩阵.若α1，α2线性无关，且α3=-α1+2α1，则线性方程组Ax=0的通解为________.

答案：
解析：

1、k(1，-2，1)^T，k为任意常数
第19题：

设A=(aij)是三阶非零矩阵，｜A｜为A的行列式，Aij为aij的代数余子式，若aij+Aij=0(i，j=1，2，3)，则｜A｜=________.

答案：1、-1.
解析：
第20题：

已知矩阵A=

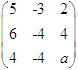
的两个特征值为λ1=1，λ2=3，则常数a和另一特征值λ3为（　　）。

A、 a=1，λ3=-2
B、 a=5，λ3=2
C、 a=-1，λ3=0
D、 a=-5，λ3=-8

答案：B
解析：
矩阵A的特征行列式和特征方程具体计算如下：

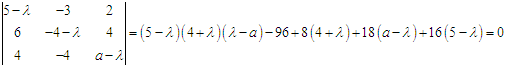
将λ1=1代入特征方程，解得：a=5；由特征值性质：λ1+λ2+λ3=5-4+a，得λ3=2。
第21题：

设λ1，λ2是矩阵A的两个不同的特征值，对应的特征向量分别为α1，α2，则α1，A(α1+α2)线性无关的充分必要条件是(　　)。

A、λ1=0
B、λ2=0
C、λ1≠0
D、λ2≠0

答案：D
解析：
第22题：

设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是( )。
A. α是矩阵-2A的属于特征值-2λ的特征向量

D. α是矩阵AT的属于特征值λ的特征向量

答案：D
解析：
提示：显然A、B、C都是正确的。
第23题：

单选题
设A是三阶矩阵，α1=（1，0，1）T，α2=（1，1，0）T是A的属于特征值1的特征向量，α3=（0，1，2）T是A的属于特征值-1的特征向量，则：（）
A
α1-α2是A的属于特征值1的特征向量
B
α1-α3是A的属于特征值1的特征向量
C
α1-α3是A的属于特征值2的特征向量
D
α1+α2+α3是A的属于特征值1的特征向量

正确答案： A
解析：暂无解析

设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆 B.矩阵A的迹为零 C.特征值-1,1对应的特征向量正交 D.方程组AX=0的基础解系含有一个线性无关的解向量

题目

相似考题

参考答案和解析

更多“设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().”相关问题

相关内容