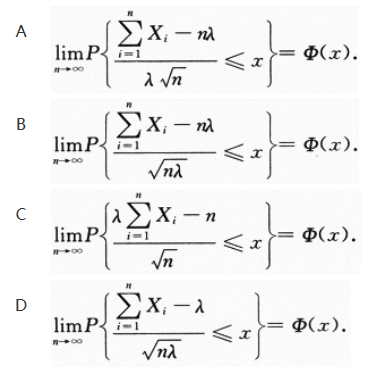
设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则

题目
设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则


相似考题

1.设随机变量X1,X2,…,X100相互独立且都服从参数为4的泊松分布,则它们的算术平均值小于等于4.392的概率为()。A、0.975B、0.95C、0.875D、0.825

2.设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。A．有相同的数学期望B．有相同的方差C．服从同一指数分布D．服从同一离散型分布

3.设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( ) A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差 B.X1,X2,…,Xn,…同分布且有相同的数学期望 C.X1,X2,…,Xn,…为同分布的离散型随机变量 D.X1,X2,…,Xn,…为同分布的连续型随机变量

4.已知总体X服从参数为λ的指数分布,设X1,X2,…,Xn是子样观察值,求λ的极大似然估计。

更多“设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则 ”相关问题

  • 第1题：

    设随机变量X1，X2，…，Xn相互独立，Sn=X1，X2，…，Xn则根据列维林德伯格(Levy-Lindberg)中心极限定理，当n充分大时，Sn近似服从正态分布，只要1，X2，…，Xn

    A.有相同的数学期望.
    B.有相同的方差.
    C.服从同一指数分布.
    D.服从同一离散分布.

    答案：C
    解析：
    【简解】本题是数四的考题，答案应选(C).

  • 第2题：

    设总体X服从参数λ的指数分布，X1，X2，…，Xn是从中抽取的样本，则E(X)为( )。



    答案：A
    解析：
    由于x服从指数分布，即



    所以

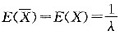
  • 第3题：

    设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.


    答案：
    解析：

  • 第4题：

    设随机变量X服从参数为A的指数分布,则P{X>)=_______.


    答案：
    解析：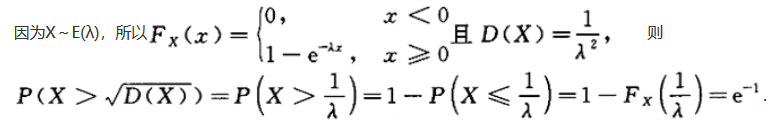

  • 第5题：

    设总体X,Y相互独立且都服从N（μ,σ^2）分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明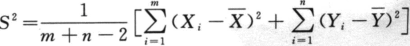：为参数σ^2的无偏估计量,


    答案：
    解析：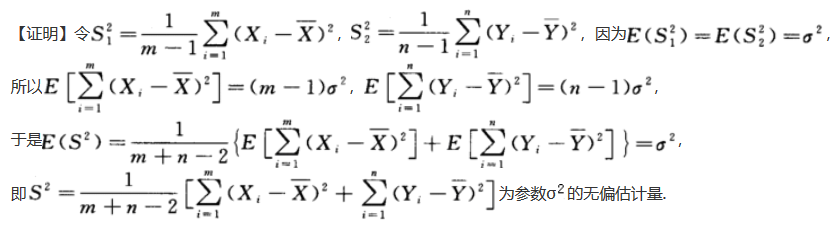

  • 第6题：

    设X1,X2,…,Xn是来自总体X的简单随机样本,已知E(X^k)=ak(k=1,2,3,4).
    　　证明：当n充分大时,随机变量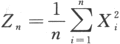近似服从正态分布,并指出其分布参数.


    答案：
    解析：

  • 第7题：

    设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X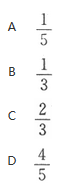


    答案：A
    解析：
    X～E(1)，Y～E(4)且相互独立，所以(X，Y)的概率密度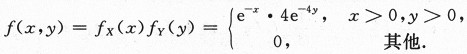　　
    　　利用公式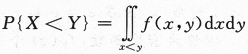可以计算出结果.
    　　【求解】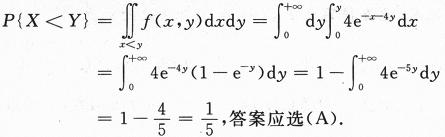

  • 第8题：

    设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。

    • A、1
    • B、3

    正确答案:D

  • 第9题：

    关于中心极限定理的描述正确的是：（）。

    • A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布
    • B、正态样本均值服从分布N（μ，σ2/n）
    • C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布
    • D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布

    正确答案:A,B,C,D

  • 第10题：

    填空题
    设随进变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ=3的泊松分布，记随机变量Y=X1-2X2+3X3，则D（Y）=____.

    正确答案： 46
    解析：
    ∵X1～U[0，6]　　　X2～N[0，22]　　　X3～P（3）
    ∴D（X1）=62/12=3　　　D（X2）=22=4　　　D（X3）=3
    又X1，X2，X3相互独立，故
    ∴D（Y）=D（X1-2X2+3X3）=D（X1）+4D（X2）+9D（X3）=3+4×4+9×3=46

  • 第11题：

    填空题
    设随机变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ＝3的泊松分布，记随机变量Y＝X1－2X2＋3X3，则D（Y）＝____。

    正确答案： 46
    解析：
    ∵X1～U[0，6]，X2～N[0，22]，X3～P（3）。
    ∴D（X1）＝62/12＝3，D（X2）＝22＝4，D（X3）＝3。
    又X1，X2，X3相互独立，故D（Y）＝D（X1－2X2＋3X3）＝D（X1）＋4D（X2）＋9D（X3）＝3＋4×4＋9×3＝46。

  • 第12题：

    填空题
    若随机变量X1，X2，X3相互独立且服从于相同的0-1分布，P{X＝1}＝0.7，P{X＝0}＝0.3，则随机变量Y＝X1＋X2＋X3服从于参数为____的____分布，且E（Y）＝____。D（Y）＝____。

    正确答案： 3,0.7,二项,2.1,0.63
    解析：
    由0-1分布与二项分布之间联系可得Y～B（3，0.7），则E（Y）＝3×0.7＝2.1，D（Y）＝3×0.7（1－0.3）＝0.63。

  • 第13题：

    设随机变量X与Y相互独立且都服从参数为A的指数分布,则下列随机变量中服从参数为2λ的指数分布的是().

    A.X+y
    B.X-Y
    C.max{X,Y}
    D.min{X,Y}

    答案：D
    解析：

  • 第14题：

    36.设Xi(i =1, 2,…,n)为n个相互独立的随机变量，则下列结论成立的是（ ）。
    A.若Xi(i =1, 2,…,n)服从正态分布，且分布参数相同，则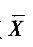服从正态分布
    B.若Xi(i =1, 2,…,n)服从指数分布，且λ相同，则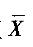服从正态分布
    C.若Xi(i =1, 2,…,n)服从[a，b]上的均勻分布，则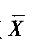服从正态分布
    D.无论Xi(i =1, 2,…,n)服从何种分布，其均值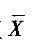都服从正态分布


    答案：A
    解析：
    若总体服从正态分布，无论样本量大小，其样本均值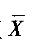都服从正态分布。

  • 第15题：

    设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时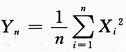，依概率收敛于_______.


    答案：
    解析：
    本题是数三的考题，根据切比雪夫大数定律或者辛钦大数定律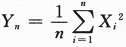，依概率收敛于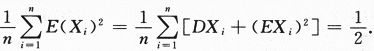答案应填

  • 第16题：

    设总体X服从分布N(0，2^2)，而X1，X2，…，X15是来自总体X的简单随机样本，则随机变量服从_______分布，参数为________.


    答案：1、F 2、(10，5)
    解析：
    本题是数三的考题，由于X～N(0，2^2)，则　
    且相互独立，故

    答案应填服从F分布，参数为(10，5).

  • 第17题：

    设随机变量X服从参数为λ的指数分布，则=_______.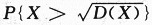


    答案：
    解析：
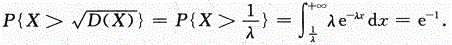    答案应填e.

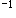
  • 第18题：

    设随机变量X服从参数为λ的指数分布,且E［（X-1）(X+2)］=8,则λ=_______.


    答案：
    解析：
    由随机变量X服从参数为λ的指数分布，得，于是，而，解得λ=.

  • 第19题：

    设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=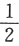.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

    A.A0
    B.1
    C.2
    D.3

    答案：D
    解析：

  • 第20题：

    设随机变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2服从正态分布N（0，22），X3服从参数为λ=3的泊松分布，记Y=X1-2X2+3X3。则DY=（）。


    正确答案:46

  • 第21题：

    设X1，X2，…，Xn是从总体X中抽取的容量为n的一个样本，如果由此样本构造一个函数T（X1，X2，…，Xn），不依赖于任何未知参数，则函数T（X1，X2，…，Xn）是一个（）


    正确答案:统计量

  • 第22题：

    问答题
    设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。

    正确答案：
    利用数学归纳法。
    当k=2时,X1+X2=Z~B(2,p)。
    假设当k=n-1时,X1+X2+…+Xn-1=Z1~B(n-1,p)。
    则当k=n时,Z=(X1+X2+…+Xn-1)+Xn=Z1+Xn,Z~B(n-1+1,p),即Z~B(n,p)。
    解析： 暂无解析

  • 第23题：

    单选题
    设随机变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ＝3的泊松分布，记随机变量Y＝X1－2X2＋3X3，则D（Y）＝（　　）。
    A

    56

    B

    48

    C

    72

    D

    46


    正确答案： B
    解析：
    ∵X1～U[0，6]，X2～N[0，22]，X3～P（3）。
    ∴D（X1）＝62/12＝3，D（X2）＝22＝4，D（X3）＝3。
    又X1，X2，X3相互独立，故D（Y）＝D（X1－2X2＋3X3）＝D（X1）＋4D（X2）＋9D（X3）＝3＋4×4＋9×3＝46。

相关内容